密码学

理论基础

Alice 给 Bob 发消息，保护消息的 confidentiality. 传输途径可以是任意的，Internet, USB stick… 在过程中被动的监听者Eve 有可能会监听或者解释信息.

在过去，军事加密依赖于信息的混乱程度 obfuscation of message contents. 现代密码学依赖于 Kerckhoff’s Principle, 除了key所有信息都是已知的.

A crypto system should be secure, even if everything about the system, except the key, is public knowledge.

信息加密是通过 encryption schemes 使用一个key和lock concept来实现的. 只有key的持有者可以加密解密信息. Alice会把key \(k\) 分享给Bob, 我们现在还不关系这个怎样实现.

• Alice 加密信息 \(m\), \(c := E(k,m)\)
• Bob 解密信息 \(m:=D(k,c)\)

香农密码 Shannon Cipher

我们定义一个 encryption scheme \(\Pi:=(E, D)\) 是一对加密解密函数

• \(k \in \mathcal{K}\) 是加密使用的key

• \(m \in \mathcal{M}\) 是信息 message

• \(c \in \mathcal{C}\) 是密文 ciphertext

• \(E: \mathcal{K} \times \mathcal{M} \rightarrow \mathcal{C}\) 是加密函数

• \(D: \mathcal{K} \times \mathcal{C} \rightarrow \mathcal{M}\) 是解密函数

• 正确性: \(\forall k \in \mathcal{K}, m \in \mathcal{M}: D(k, E(k, m))=m\)

这个密码被称为 Shannon cipher.

One-time-pad (OTP)

OTP 是一个Shannon cipher. OTP 中 \(\mathcal{K}=\mathcal{M}=\mathcal{C}:=\{0,1\}^L\) 其中 \(L\ge 1\) 是长度. 我们可以简单证明它的正确性

证明 \[ D(k, E(k, m))=D(k, k \oplus m)=k \oplus(k \oplus m)=m \]

定义 1 完美安全 Perfect security

一个Shannon cipher \(\Pi=(E, D)\) over \((\mathcal{K}, \mathcal{M}, \mathcal{C})\) 是 perfectly secure 若 \[ \forall m_0, m_1 \in \mathcal{M}, c \in \mathcal{C}: \operatorname{Pr}\left[E\left(\mathbf{k}, m_0\right)=c\right]=\operatorname{Pr}\left[E\left(\mathbf{k}, m_1\right)=c\right] \] \(\mathbf{k}\) 是 random variable.

任取两个信息，用任意个key得出密文是 \(c\) 的概率是相同的. 也就是可能是 \(m_0\) 也可能是 \(m_1\)

于是不可能从密文中获取任何信息. 我们一直假设 \(k\) 是完全随机选取的，每个 \(k\) 的概率是 \(\frac{1}{|\mathcal{K}|}\) 于是可以推出 \[ \operatorname{Pr}[E(k, m)=c]=\frac{N_{m, c}}{|\mathcal{K}|} \] 其中 \(N_{m,c}\) 是有多少个key 可以把 \(m\) 加密成 \(c\) \[ N_{m, c}=|\{k \in \mathcal{K}: E(k, m)=c\}| \] 所以有另一个等价的定义： \[ \forall m_0, m_1 \in \mathcal{M}, c \in \mathcal{C}: N_{m_0, c}=N_{m_1, c} \] 对于任意两个信息，能把 \(m_0\) 变成 \(c\) 和能把 \(m_1\) 变成 \(c\) 的key个数相同

• 即使Perfectly secure 的密码也可能被破解，如果使用不当，比如OTP只能用1次.

定理 1 OTP perfectly secure

The one-time pad is perfectly secure.

因为对于所有 \(m \in \mathcal {M}\) 只有1个 key 使得 \(E(k,m)=c\) 也就是 \(N_{m,c}=1\) .

证明

假设有两个 key \(k_0,k_1\) 使得 \(E(k_0,m)=E(k_1,m)=c\) 那么 \[ \begin{aligned} E\left(k_0, m\right) & =E\left(k_1, m\right) \\ k_0 \oplus m & =k_1 \oplus m \\ k_0 \oplus m \oplus m & =k_1 \oplus m \oplus m \\ k_0 & =k_1 \end{aligned} \] 所以这两个是一样的,

但在使用中，如果要通讯 1GB, 那么你需要交换 1GB 的密钥. 那还不如只交换信息.

定理 2 Shannon’s Theorem

If \(\Pi=(E, D)\) 是 perfectly secure, then \(|\mathcal{K}| \geq|\mathcal{M}|\)

证明

假设 \(|\mathcal{K}| < |\mathcal{M}|\) 那么选择一个信息和密钥 \(\operatorname{Pr}\left[E\left(\mathbf{k}, m_0\right)=c\right]>0\) 然后设 \(S\) 是所有 \(c\) 的解密集合. \(S=\{D(\hat{k}, c) \in \mathcal{M}: \hat{k} \in \mathcal{K}\}\) 有 \(|S| \leq|\mathcal{K}|<|\mathcal{M}|\) 那么我们选择 \(m_1 \in \mathcal{M} \backslash S\) 所以\(m_1\) 不是 \(c\) 的解密。那么 \(c\) 也不是 \(m_1\) 的加密，因为如果是的话根据正确性一定是解密。所以 \(\operatorname{Pr}\left[E\left(\mathbf{k}, m_1\right)=c\right]=0\) 所以不能被加密或解密。所以找到了一个不同的概率。

所以 perfect security 是不可实现的 not practical. 我们需要一个高效的算法使得我们的密码被高效破译的可能性忽略不计.

定义 2 PPT adversary

一个对手 adversary \(\mathcal{A}\) 是高效的 efficient, 若它可以在多项式时间内完成计算 polynomially-bounded time. 我们称它为 probabilistic polynomial time (PPT)-adversary.

定义 3 polynomially-bounded

一个函数 \(f: \mathbb{Z}_{+} \rightarrow \mathbb{R}\) 是 polynomially-bounded 若存在 \(c\in \mathbb{N}\) 使得对于所有整数 \(n \geq n_0\), we have \(|f(n)| \leq n^c\left(f(n) \in \mathcal{O}\left(n^c\right)\right)\)

定义 4 negligible

一个函数 \(f: \mathbb{Z}_{+} \rightarrow \mathbb{R}\) 是 negligible 若对于所有 \(c\in \mathbb{N}\) 存在 \(n_0 \in \mathbb{Z}_{+}\) 使得对于所有整数 \(n \geq n_0\) 有 \(|f(n)| \leq \frac{1}{n^c}\left(f(n) \in \mathcal{O}\left(\frac{1}{n^c}\right)\right)\)

定义 5 super-poly

一个函数 \(f: \mathbb{Z}_{+} \rightarrow \mathbb{R}\) 是 super-poly 如果 \(\frac{1}{f}\) 是negligible.

计算法则

image-20230422154435525

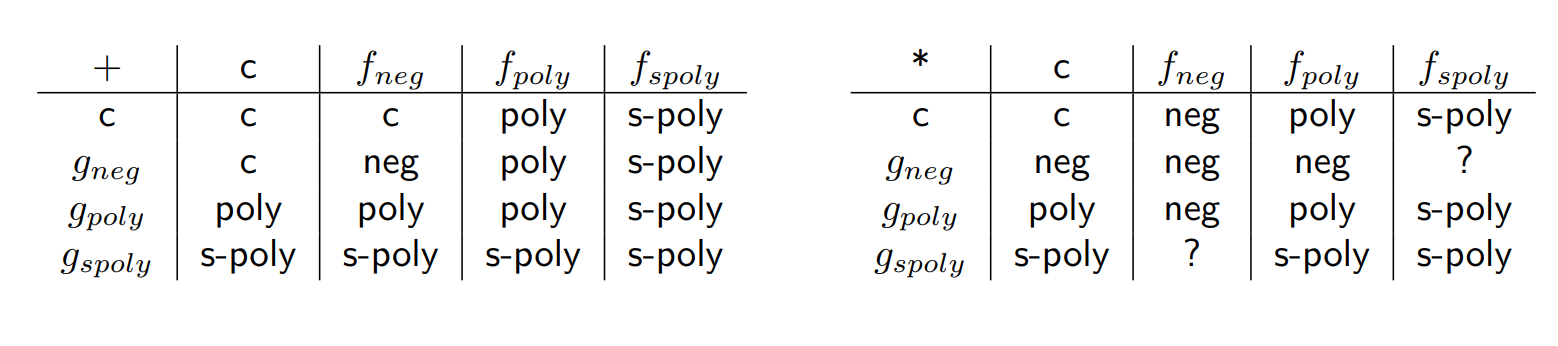
安全参数 Security Parameters

• Security parameter \(\lambda\) 是一个正整数

​ 它在密码部署的时候选择，等级越高，安全系数越高. 越高意味着更长的key和更慢的 \(D,E\) 运行时间

• System parameter \(\Lambda\) 是一个bit string

​ 是被 \(\lambda\) 选择的. 比如是一个模数用于取模.

定义 6 Efficient Algorithm

\(A\) 是一个算法，输入一个 security parameter \(\lambda\) 和其他的参数. 他们被表示为一个bit string \(x \in\{0,1\}^{\leq p(\lambda)}\) 其中 \(p\) 是一个fixed polynomial. 那么我们说 \(A\) 是efficient algorithm 若存在一个 poly-bounded function \(t\) 和一个可以忽略的参数 negligible function \(\epsilon\) 使得对于所有的 \(\lambda,x\) 这个运行时间超过 \(t(\lambda)\) 的概率最多是 \(\epsilon(\lambda)\)

定义 7 Computational Cipher

我们定义一个 computational cipher 是一对高效算法 \((E, D)\) 是一对加密解密算法

• \(k \in \mathcal{K}\) 是加密使用的key

• \(m \in \mathcal{M}\) 是信息 message

• \(c \in \mathcal{C}\) 是密文 ciphertext

• \(E: \mathcal{K} \times \mathcal{M} \rightarrow \mathcal{C}\) 是加密算法

• \(D: \mathcal{K} \times \mathcal{C} \rightarrow \mathcal{M}\) 是解密算法

• \(\mathcal{K,M,C}\) 是有限的空间

我们的加密算法有可能是 prababilistic 的，也就是对于给定的 \(k,m,E(k,m)\) 可能会有很多结果. \[ c \stackrel{R}{\leftarrow} E(k, m) \] 正确性可以这样写： \[ \forall c \stackrel{R}{\leftarrow} E(k, m): D(k, c)=m \] 所有deterministic cipher都是 Shannon cipher.

然而 Shannon cipher不一定是 computational cipher (不一定高效算法)

反过来也不一定 (有可能是prababilistic)

computaional cipher 的安全性

有可能没有 \(m_0\) 加密成 \(c\) 所以我们令 \[ \left|\operatorname{Pr}\left[\phi\left(E\left(\mathbf{k}, m_0\right)\right)\right]-\operatorname{Pr}\left[\phi\left(E\left(\mathbf{k}, m_1\right)\right)\right]\right| \leq \epsilon \] 我们可以通过 Attack Game 来定义 \(\epsilon\)

Attack Game 1

我们有2个Experiment 0, 1 对于 \(b \in\{0,1\}\) 我们定义 Experiment \(b\)

• 对手计算 \(m_0,m_1\in \mathcal{M}\) 长度相同，给chanllenger
• challenger 计算 \(k \stackrel{R}{\leftarrow} \mathcal{K}, c \stackrel{R}{\leftarrow} E\left(k, m_b\right)\) 然后把 \(c\) 发给对手
• 对手猜测 \(m_{\hat{b}}=D(k, c)\) 是哪一个信息.

我们定义 \(\mathcal{A}\) 的 semantic security advantage 为 \[ S C a d v[\mathcal{A}, \Pi]:=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \]

目的是A 不能区分实验0和1, 如果 A 可以区分，那么A的输出b分布肯定不一样。因为是0，1两个变量，所以分布就用1的概率来表示，所以作差

定义 8 semantic security

一个 cipher 是 semantically secure 若 \(Scadv[\mathcal{A},\Pi]\) 对于所有 PPT 对手是可忽略不计的 negligible.

Bit Guessing

image-20240512195906404

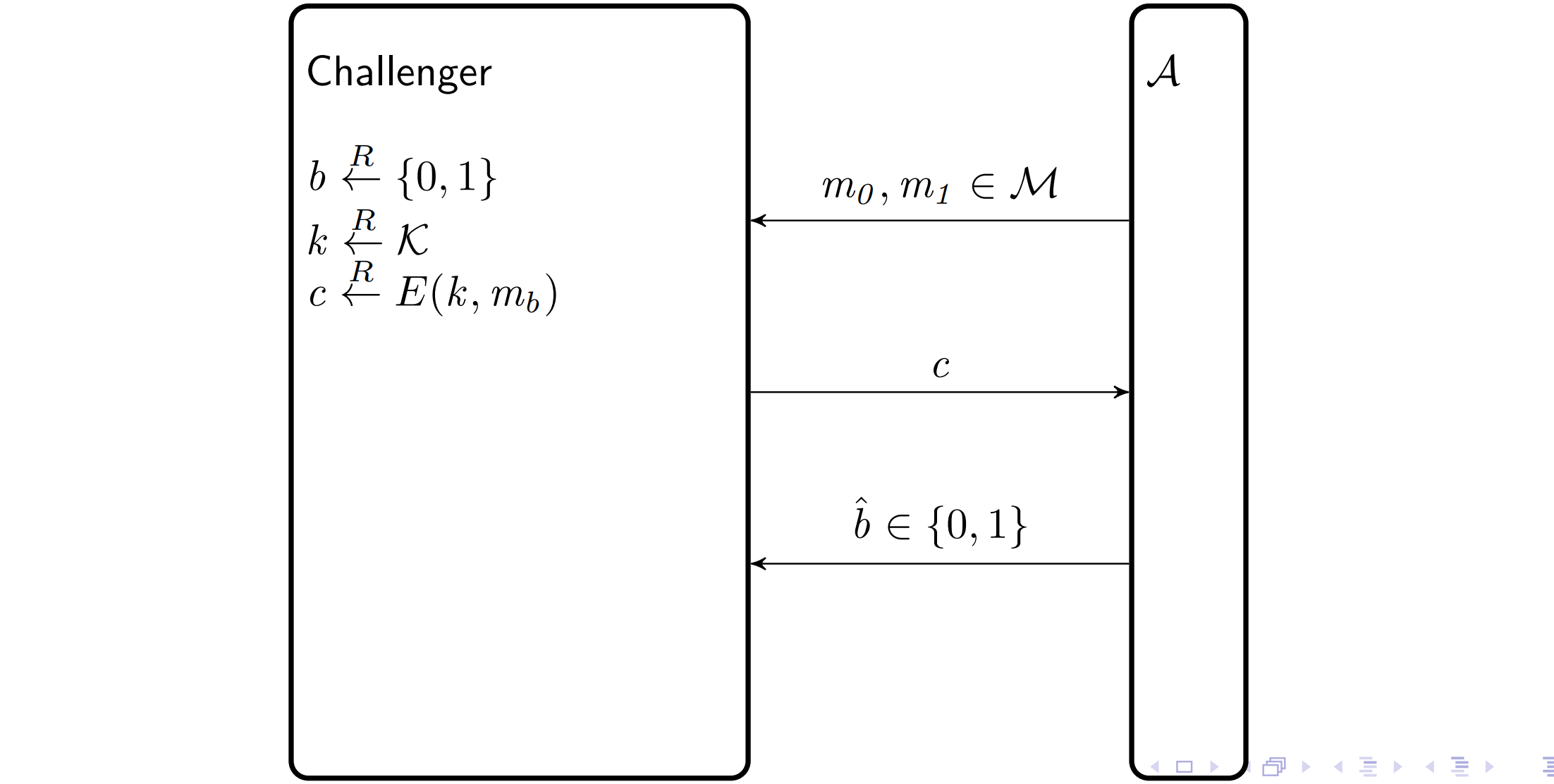
• \(\mathcal{A}\) 计算 \(m_0,m_1 \in \mathcal{M}\) ，给chanllenger
• challenger 计算 \(b \stackrel{R}{\leftarrow}\{0,1\}, k \stackrel{R}{\leftarrow} \mathcal{K}, c \stackrel{R}{\leftarrow} E\left(k, m_b\right)\)
• \(\mathcal{A}\) 猜测 \(m_{\hat{b}}=D(k, c)\) 发送 \(\hat{b}\)

\(\mathcal{A}\) 获胜的事件是 \(W\)

We define \(\mathcal{A}\) 的 bit-guessing advantage as \[ S C a d v^*[\mathcal{A}, \Pi]:=\left|\operatorname{Pr}[W]-\frac{1}{2}\right| \]

他比guessing好多少

两者关系 \[ \begin{aligned} S C a d v^*[\mathcal{A}, \Pi] & =\frac{1}{2} * S C a d v[\mathcal{A}, \Pi] \end{aligned} \]

Secret key cryptography

定义 10 Pseudo-random generator

我们定义一个 pseudo-random generator (PRG) 是 \[ G: \mathcal{S} \rightarrow \mathcal{R} \] 其中

• \(\mathcal{S}:=\{0,1\}^l\) is called the seed space.
• \(\mathcal{R}:=\{0,1\}^L\) is called the output space.
• \(l < L\)
• 对于随机选择的 \(s \stackrel{R}{\leftarrow} \mathcal{S}\) 和 \(r \stackrel{R}{\leftarrow} \mathcal{R}, G(s)\) and \(r\) 是 computationally indistinguishable 的

image-20240512195932397

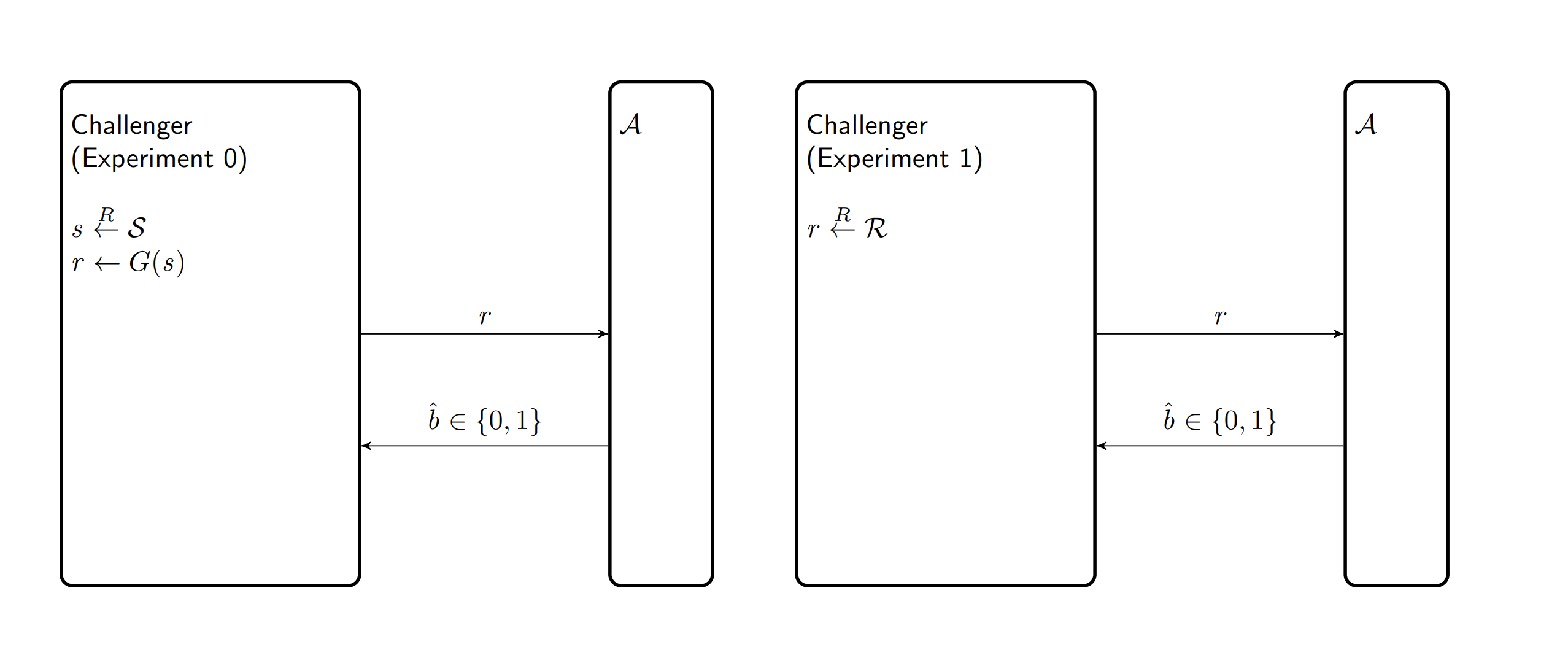
Attack Game 3 PRG advantage

对于一个 PRG \(G\) , 定义实验0，1

• b=0, challenger 计算 \(s \stackrel{R}{\leftarrow} \mathcal{S}, r \leftarrow G(s)\)
• b=1, \(r \stackrel{R}{\leftarrow} \mathcal{R}\)

对手回答0，1 \[ \operatorname{PRGadv}[\mathcal{A}, G]:=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \]

定义11 Secure PRG

PRG 是 secure的，若 \(P R G a d v[\mathcal{A}, G]\) 是 negligible for all PPT \(\mathcal{A}\)

Stream ciphers

使用 PRG 我们可以定义 stream cipher

• A seed \(s \in \mathcal{S}:=\{0,1\}^l\)
• A message \(m \in \mathcal{M}:=\{0,1\}^L\)
• An output \(r \in \mathcal{R}:=\{0,1\}^L\)
• A ciphertext \(c \in \mathcal{C}:=\{0,1\}^L\)
• An encryption function \(E: \mathcal{S} \times \mathcal{M} \rightarrow \mathcal{C}\)
• A decryption function: \(D: \mathcal{S} \times \mathcal{C} \rightarrow \mathcal{M}\)
• \(l < L\)

\(E(s, m):=G(s) \oplus m=r \oplus m\)

\(D(s, c):=G(s) \oplus c=r \oplus c\).

定理 3 使用PRG 构造 Semantic Secure 的Cipher

\[ S C a d v[\mathcal{A}, \Pi]=2 \cdot S C a d v v^*[\mathcal{A}, \Pi]=2 \cdot \operatorname{PRGadv}[\mathcal{B}, G] \]

构造 A 对B 是 Bit guessing, B 攻击 PRG, 如果 A 赢了，那么对PRG输出0定理 4

定理4 parallel construction PRG

取 \(n\) 次 \(s\) , 输出 \(n\) 次 \(G(s)\)， \(G^{\prime}\left(s_0, \ldots, s_{n-1}\right)=\left(G\left(s_0\right), \ldots, G\left(s_{n-1}\right)\right)\) \[ P R G a d v\left[\mathcal{A}, G^{\prime}\right]=n * P R G a d v[\mathcal{B}, G] \]

建立hybrid game, A对B是 A取前 \(w\) 个随机数, 第 \(w\) 个从 PRG 取

BM Sequential construction

有一个 \(G\) 可以生产一个新的种子和一个随机数, 通过迭代 \(n\) 次生产\(n\) 个随机数 \[ P R G a d v\left[\mathcal{A}, G_{B M}\right]=n * P R G a d v[\mathcal{B}, G] \]

One Way Function

给 A 一个 \(y\) , 让A求出 \(x\) \[ O W F a d v[\mathcal{A}, f]=\operatorname{Pr}[y=f(\hat{x})] \]

hard-core bit

给 A 一个 \(y\), 让 A 求 \(hc(x)\) \[ H C a d v[\mathcal{A}, f]=\left|\operatorname{Pr}[\hat{b}=h c(x)]-\frac{1}{2}\right| \]

构造OWP PRG

\(f\) 是 one way permutation, \(hc\) 是 hard core bit, PRG \(G(x):=(f(x), h c(x))\) is secure.

• one way permutation \(f(x)\) doesn’t change distribution of \(x\)
• 假设A可以计算 \(hc(x)\) , 我们可以猜一个 \(b\) 如果 A 说这是0，那么就是猜对的，否则就是猜错的 （有点复杂）

CPA Security

image-20240711145130097

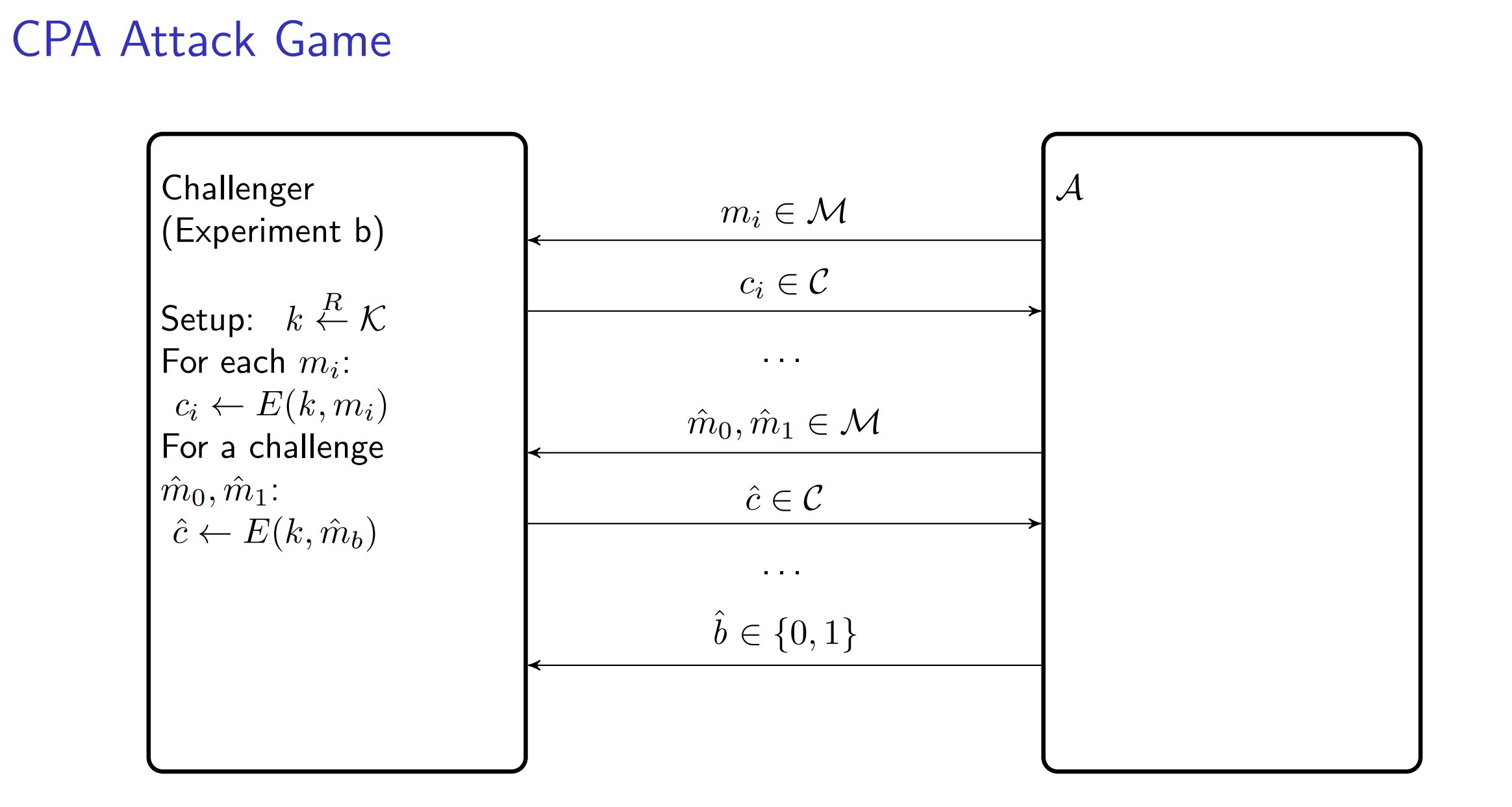
Theorem 8

\(\Pi_{r C T R}\) using a secure PRF is CPA secure \[ C P \operatorname{Aadv}\left[\mathcal{A}, \Pi_{r C T R}\right] \leq 2 \cdot \frac{Q 2 l}{|\mathcal{X}|}+2 \cdot \operatorname{PRFadv}[\mathcal{B}, F] \]

构造bit guessing game，把 PRF 换成 \(f\) , 最后再换成\(f\), 但是最后一步随机数. 用Difference lemma计算冲突概率

PRF

pseudo-random function, 用一个 \(k\) , \(F(k,x)\) 和 random function 没有区别

attack game

A可以询问 C 任意次，区分PRF 和 random function \[ \operatorname{PRFadv}[\mathcal{A}, F]=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \]

tree construction

用一个 01Trie, 返回对应叶子的值，父亲节点生产子节点的值，根是随机数 \[ P R F a d v[\mathcal{A}, F]=Q l \cdot P R G a d v[\mathcal{B}, G] \]

hybrid game, 第k层的所有叶子用一个 parallel construction 的 PRG 代替

CCA Security

image-20240711145019609

PRP

是permutation

attack game

A可以询问 \(x\) 给出 \(y\), 询问 \(y\) 给出 \(x\), 使得它和随机permutation无法区分

weak PRP

A 不能问 \(y\)

构造 CCA secure Cipher

\(E(k,m) = P(k, m||r)\), 把一个 \(r\) 随机树加在后面，然后P映射一下

\(D(k,m)=P^{-1}(k,c)\) 取前几位 \[ C C A a d v^*[\mathcal{A}, \Pi] \leq P R P a d v[\mathcal{B}, P]+\frac{Q_D}{2^{2 n}}+\frac{Q_E}{2^n} \]

用bit Guessing game, reduce to PRP, 然后difference lemma

permutation

Luby-Rackoff construction

Feistel permutation

\(x \oplus f(y)\) 然后交换位置

image-20240720234229312

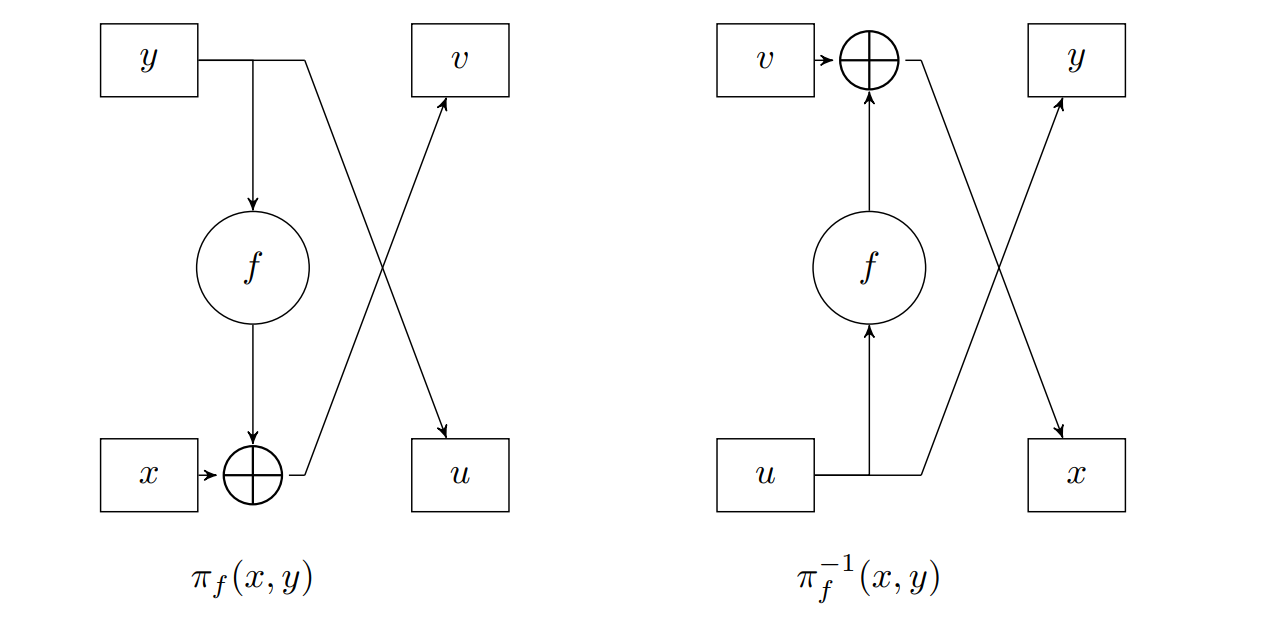
Luby-Rackoff

4 round Feistel network \[ P R P a d v[\mathcal{A}, E] \leq 4 \cdot P R F a d v[\mathcal{B}, F]+\frac{Q^2}{|\mathcal{X}|} \]

证明有点难

DES 是 16 round Feistel network

PRF Switching Lemma

weak PRP 和 PRF 的区别很小 \[ |w P R P a d v[\mathcal{A}, P]-P R F a d v[\mathcal{A}, P]| \leq \frac{Q^2}{2|\mathcal{X}|} \]

这两者Experiment 0 相同，区别在于真随机函数和真随机排列的区别，所以取\((i,j)\) \(f(i)=f(j)\) 相等的概率来区分

CI

A cipher provides ciphertext integrity, if CIadv is negligible for all PPT adversaries A.

Attack Game CI

A 询问 \(m_i\), C 回答 \(c_i = E(k,m_i)\)

A 发送一个 \(c\), 如果 C 可以解密，那A赢

AE

A cipher provides authenticated encryption, if it is CPA-secure and provides ciphertext integrity under all PPT adversaries A.

Theorem 15 AE implies CCA

If a cipher Π is AE-secure, then it is CCA-secure. \[ C C A a d v[\mathcal{A}, \Pi] \leq 2 Q_d \cdot C \operatorname{Iadv}\left[\mathcal{B}_{C I}, \Pi\right]+C P \operatorname{Aadv}\left[\mathcal{B}_{C P A}, \Pi\right] \]

用0->1的思路构造，Game0是CCA的Exp0, Game1是如果解密不在 \(m_i\) 里那么reject. \(|p_0 - p_1|\le p_{Z}\) . \(Z\) 就是A成功解密的时候

MAC

S : 计算加密的算法

V: 验证tag的算法，\(V(k,m,t)\) 验证 \(S(k,m)==t\) 是否成立

Attack Game MAC

A 询问 tag的计算

A 给出一个 tag的仿制品, 如果验证成功则 A 胜利

SUF-CMA

如果是MAC secure 那么 strong existential unforgeability under a chosen message attack

EUF-CMA

existential unforgeability under chosen message attack

只要A可以生成伪造 \((m,t)\) 且 \(m\) 不在询问中

定理 16

\(F\) 是 secure PRF, \(\mathcal{T}\) superpoly, 那么 MAC 是secure的 \[ \begin{aligned} S(k, m) & :=F(k, m) \\ V(k, m, t) & := \begin{cases}\text { accept } & \text { if } F(k, m)=t \\ \text { reject } & \text { otherwise. }\end{cases} \end{aligned} \]

Game0 用 F(k,m), Game1 用 f(m), Game1只能猜, 所以\(M A C a d v[\mathcal{A}, \mathcal{I}]=\operatorname{Pr}\left[W_0\right] \leq\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right|+\operatorname{Pr}\left[W_1\right] \leq \operatorname{PRFadv}[\mathcal{B}, F]+\frac{1}{|\mathcal{T}|}\)

CBC

\(c_i\) 作为下一个 \(IV\)

image-20240721111112018

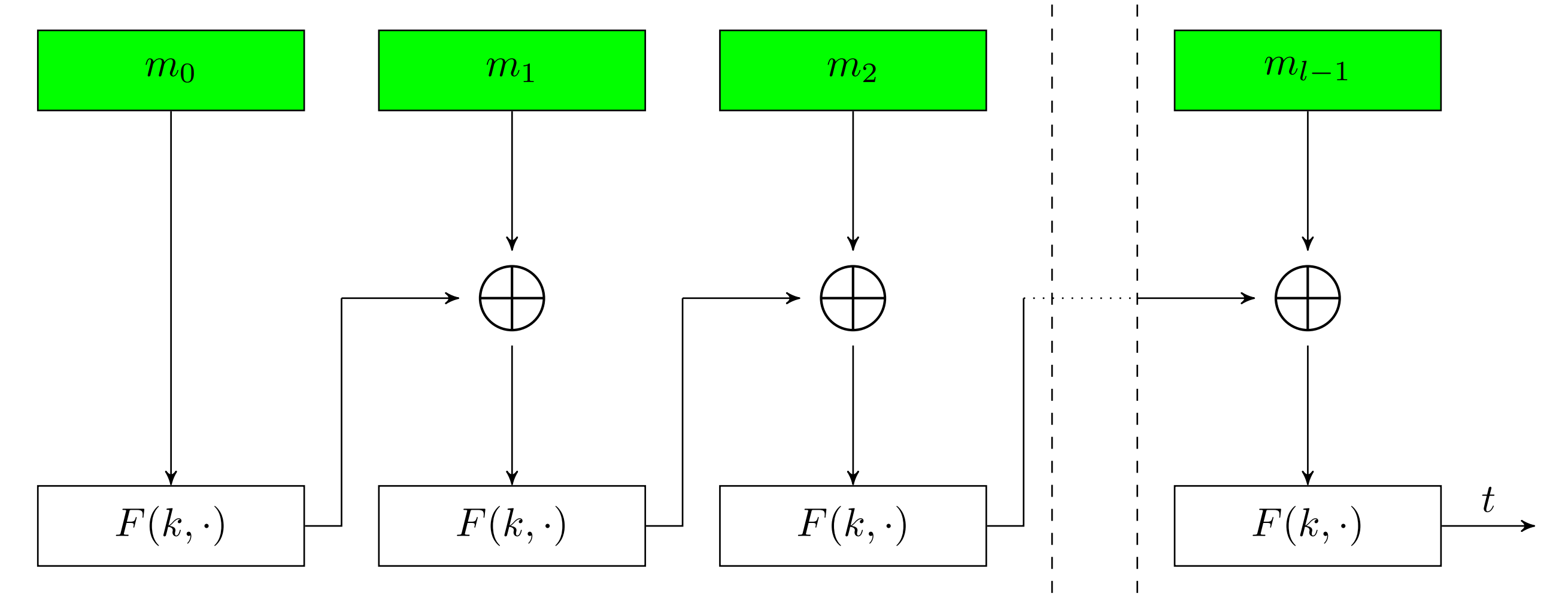
Cascade

\(c_i\) 作为下次的 \(k\)

image-20240721113300686

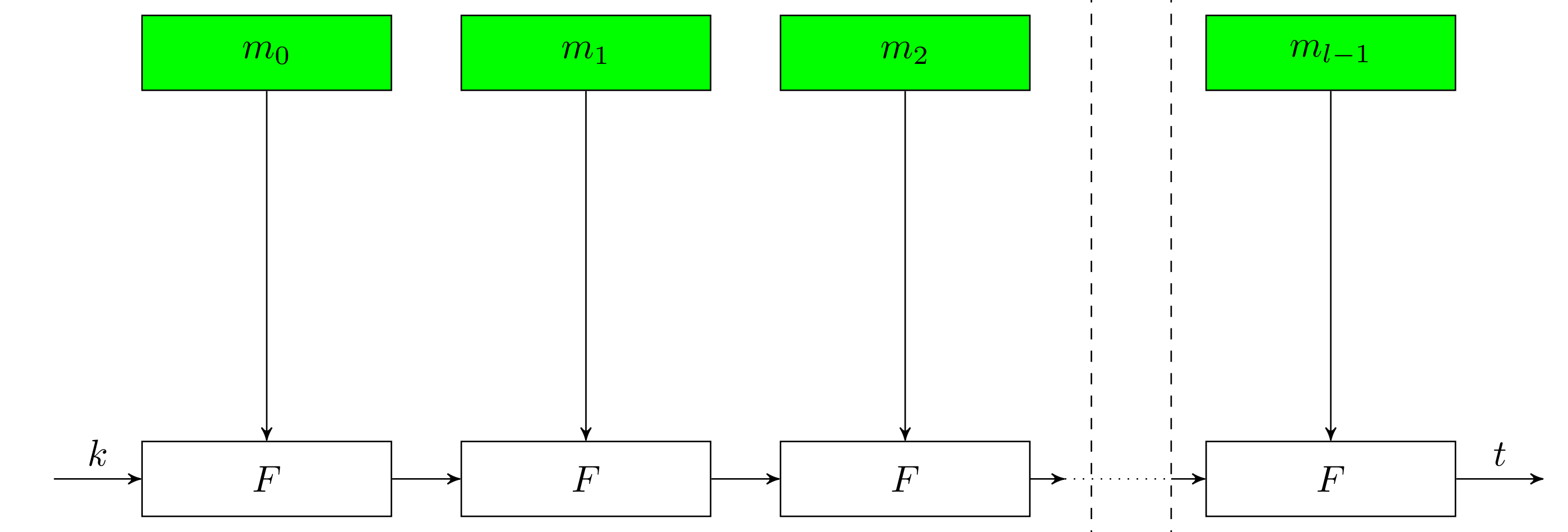
Prefix-Free

A 的每个询问可以是一个String 插入到 Trie 上

生产这样一个树，每个节点都是 randvalue, 需要检查consistency，因为 \(f( \gamma_{p^{\prime}} \oplus a^{\prime}=\gamma_p \oplus a )\) 这里可能会有重复的，相同的x肯定要映射到相同的 \(f(x)\) 上， 所以要检查

Theorem 17

secure PRF \(F\) , \(F_{CBC}\)对于prefix free A安全 \[ P R F^{p f}\left[\mathcal{A}, F_{C B C}\right] \leq \frac{(Q l)^2}{2|\mathcal{X}|}+P R F a d v[\mathcal{B}, F] \]

Game0是用Trie实现CBC, Game1是把 F换成 f. Game2 是把所有节点都变成随机，不检查冲突

定理 18

secure PRF \(F\) , \(F^{*}\)对于prefix free A安全 \[ P R F^{p f}\left[\mathcal{A}, F^*\right] \leq Q l \cdot P R F a d v[\mathcal{B}, F] \]

定理 19

\(F_{CBC},F^{*}\) 都不是安全的MAC (也不是secure PRF)

构造 \(m_p\), \(m_1\) 其中 \(m_p\) 是 \(m_1\) 的prefix, 那么 \(f_p \oplus f_1\) 可以构造出 \(m_2\) 是 \(m_1\) 的后缀

Prefix-free encoding

把 \(m = (len(m),m_0,...m_k)\) 先用长度占第一个，就是prefix free了

• not nicely support variable size messages

CMAC

\(r p f(k, m):=\left(x_0, \ldots, x_{n-2},\left(x_{n-1} \oplus k\right)\right)\) 把最后一个块异或上\(k\) , 这样prefix的概率是 \(\frac{1}{|\mathcal{X}|}\)

Encrypted PRF

用另一个PRF \(F\) 加密 \(E F\left(\left(k_0, k_1\right), m\right):=F\left(k_1, P F\left(k_0, m\right)\right)\)

用CBC是ECBC，用cascade是NMAC

• feed one block at a time to the MAC and at some point in the future decided that the message is now complete

定理 20

\(EF\) 是 secure 的PRF \[ P R F a d v[\mathcal{A}, E F] \leq P R F a d v\left[\mathcal{B}_1, F\right]+\frac{Q^2}{2}\left(P R F^{p f} a d v\left[\mathcal{B}_2, P F\right]+\frac{1}{|\mathcal{Y}|}\right) \]

Keyed Hash Function

就是有 \(k\) 作为参数的 Hash Function

Collision resistance

A 给 \(m_0,m_1\) 使得 \(H(k,m_0)=H(k,m_1)\) , A赢的概率是 \(U H F a d v[\mathcal{A}, H]\)

collision resistant keyed hash functions universal hash functions (UHFs)

Computational UHF

UHFadv是 negligible的

定理 21

\(PF\) 是extendable, prefix free PRF, 那么 \(PF\) 也是 computational UHF \[ U H F a d v[\mathcal{A}, P F] \leq P R F^{p f} a d v[\mathcal{B}, P F]+\frac{1}{|\mathcal{Y}|} \]

Game0 PF 的 UHF game, Game 1 把 PF 换成 f, 如果是 f 的话,因为是extendable，所以如果是prefix可以构造不是prefix，A只能猜，所以是1/|y|

Second-preimage resistance

C给定一个 \(m_0\), A 找出一个 \(m_1\) 使得 \(H(m_0)=H(m_1)\)

定理 22 MAC from UHF

\(H\) 是 UHF, \(F\) 是 secure PRF, 那么 \(F^{\prime}\left(\left(k_0, k_1\right), m\right):=F\left(k_1, H\left(k_0, m\right)\right)\) 是 secure PRF \[ P R F a d v\left[\mathcal{A}, F^{\prime}\right] \leq P R F a d v\left[\mathcal{B}_F, F\right]+\frac{Q^2}{2} \cdot U H F a d v\left[\mathcal{B}_H, H\right] \]

Game0是F’ 的PRF, Game1是换成f, Game2是直接返回随机数, Game1和2的区别是找\(Q\) 中的pair \((i,j)\) 是相等的，而找相等的概率是 UHFadv

Hash function

\(H(x)\) 和 keyed hash function 类似，但是没有key

Collision resistance

A 找两个 \(m_0,m_1\) 使得 \(H(m_0)=H(m_1)\) 的概率, \(C Radv[\mathcal{A}, H]\)

Second-preimage resistance

C 随机一个 \(m_0\) 发给 A, A找出与之对应的collision的概率 \(\operatorname{SPRadv}[\mathcal{A}, H]\)

H is collision resistant \(\mathbb{R}ightarrow\) H is 2nd-preimage resistant \(\mathbb{R}ightarrow\)H is one-way

DM (Davies-Meyer)

Hash for short message

把 \(m\) 分成2半，一个是 \(x\), 一个是 \(k\) 然后 \[ h_{D M}(x, k)=E(k, x) \oplus x \]

MD (Merkle-Damgård)

用一个小的hash函数 \(h\) 来构造一个大的

image-20240715161432596

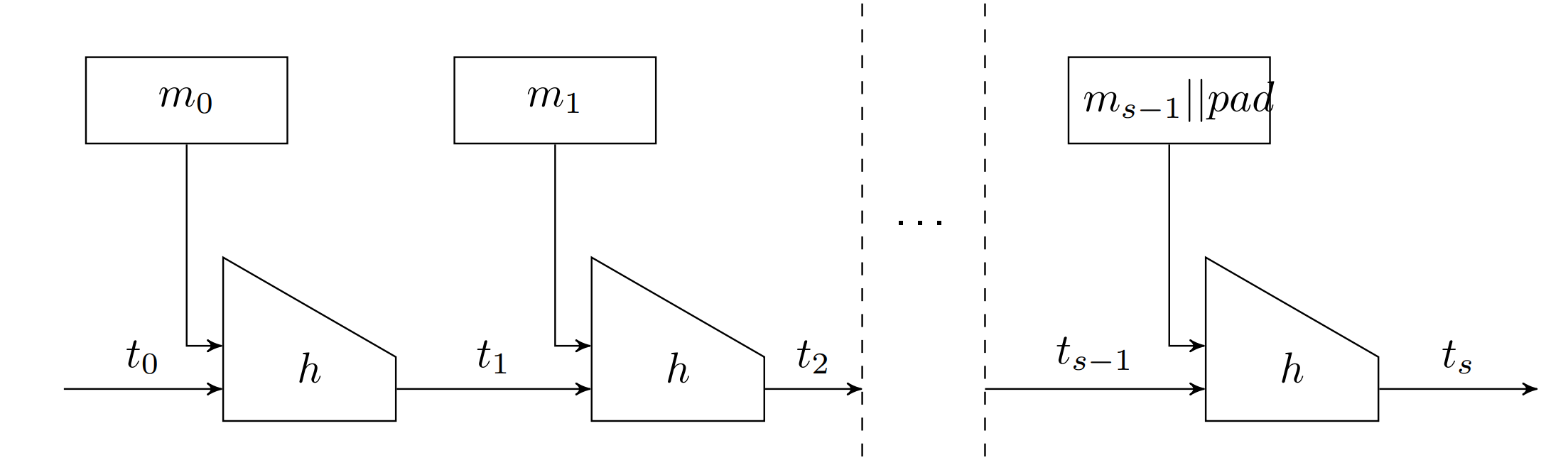
定理 23

\(h\) 是 collision-resistant , \(H_{MD}\) 也是 collision-resistant \[ C \operatorname{Radv}\left[\mathcal{A}, H_{M D}\right]=\operatorname{CRadv}[\mathcal{B}, h] \]

有一\(H_{MD}\) 的collision, 如果 \(t\) 或者 \(m\) 不一样，那么已经有一个 \(h\) 的collision, 否则可以往前推，一定可以找到

定理 24 Mac from Hash

\(\mathcal{I}:=(S, V)\) 是 secure MAC, \(H\) 是 collision resistant 那么下面这个MAC 是 secure 的 \[ S^{\prime}(k, m):=S(k, H(m)) \quad \text { and } \quad V^{\prime}(k, m, t):=V(k, H(m), t) \]

\[ M A C a d v\left[\mathcal{A}_{\mathcal{I}^{\prime}}, \mathcal{I}^{\prime}\right] \leq M A C a d v\left[\mathcal{B}_{\mathcal{I}}, \mathcal{I}\right]+C \operatorname{Radv}\left[\mathcal{B}_H, H\right] \]

分两种情况，1. A在query的时候，有2个m是collision，那么可以用来攻击CRadv, 否则可以用来攻击MACadv

Sponge construction

是用permutation \(\pi\) 来构造的 Hash , 先进行absorption

image-20240715162038326

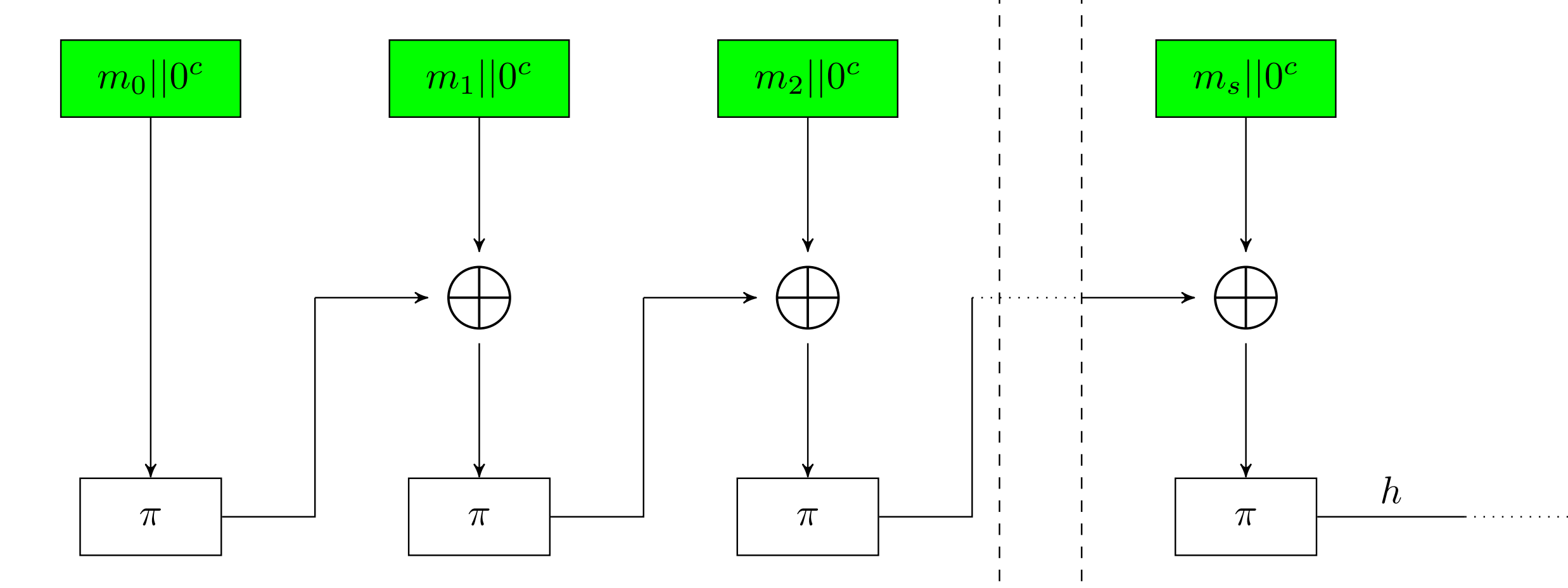
然后进行sqeeze

image-20240715162059011

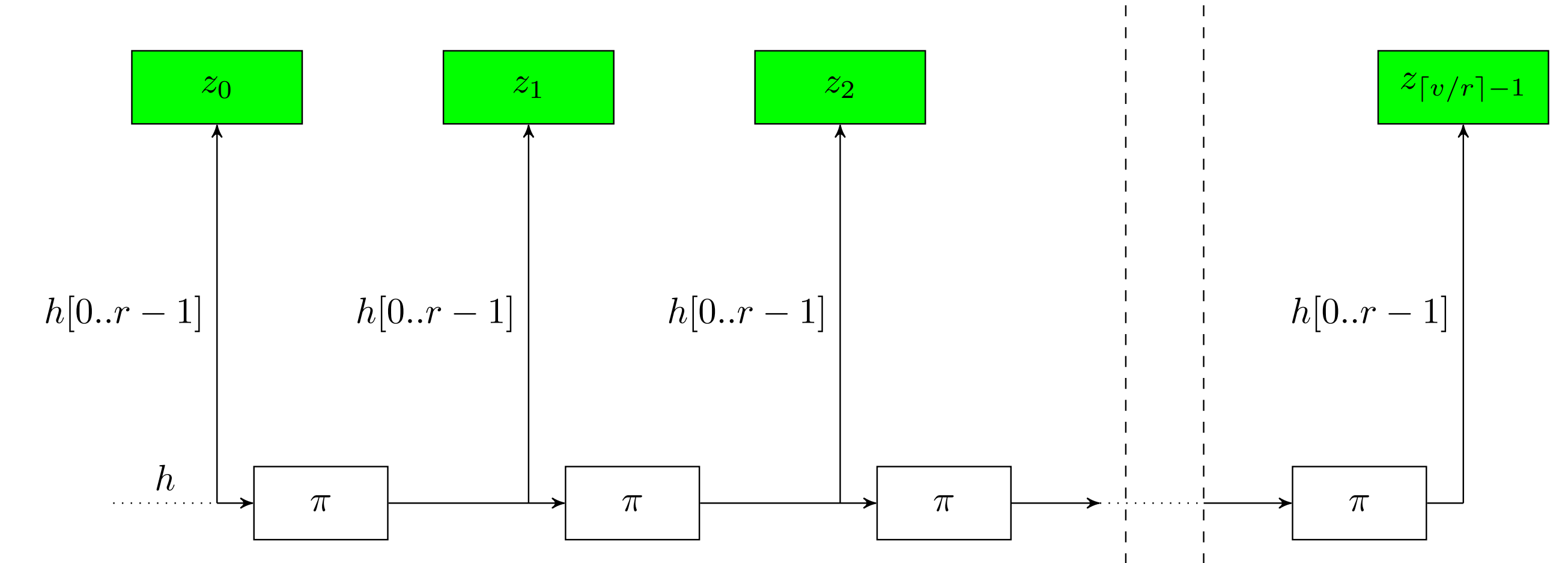
Theorem 25

若 \(\pi\) 是 random permutation, \(H\) 是 collision resistant

AE-secure construction

Encryption then MAC

secure

定理 26

\(\Pi=(E, D)\) 是 CPA secure, \(\mathcal{I}=(S, V)\) 是 secure MAC, 那么 encrypt then mac is secure \[ \operatorname{CIadv}\left[\mathcal{A}_{C I}, \Pi_{E t M}\right]=M A C a d v\left[\mathcal{B}_{M A C}, \mathcal{I}\right] \]

\[ C P \operatorname{Aadv}\left[\mathcal{A}_{C P A}, \Pi_{E t M}\right]=C P \operatorname{Aadv}\left[\mathcal{B}_{C P A}, \Pi\right] \]

直接构造就行了

AEAD

把associated data 和 c 一起 MAC

Public-key cryptography

KEM

是 \(G\) 生成 \((pk, sk)\) , 用 \((k,c) \leftarrow E_{kem}(pk)\) 生产 \(k\)，\(D_{kem}(sk, c) = k\) 解密

Attack game

C 发送 \(pk\), \((k_b,c_{kem})\) 给 A, A能否区分 \(k_b\) 和随机生成的 \(k\)

Trapdoor Function

是 \((G, F, I)\) , \(G\) 是 KEM \[ \forall(p k, s k) \stackrel{R}{\leftarrow}: \forall x \in \mathcal{X}: I(s k, F(p k, x))=x \]

One way TF, Attack Game

C 发送 \(pk,y\) 给 A, A 能否计算 \(x\) 是的 \(F(pk,x)=y\) , \(O W T F a d v[\mathcal{A}, \mathcal{T}]=\operatorname{Pr}[y=F(p k, \hat{x})]\)

用 BM construction 来构造 KEM

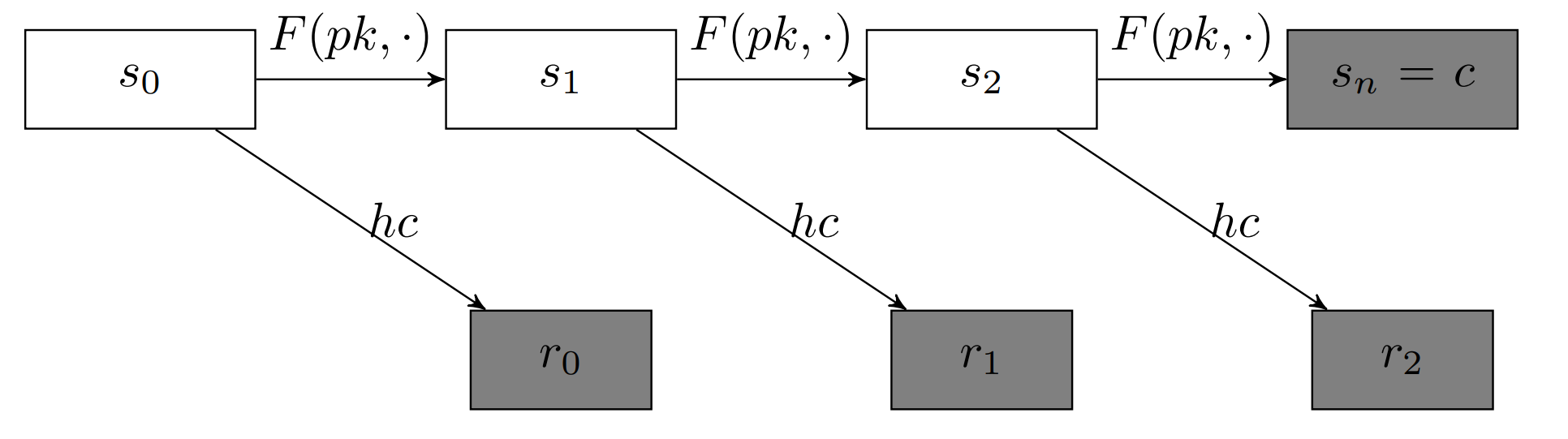\[ K E M C P A a d v\left[\mathcal{A}, \mathcal{E}_{B M}\right] \leq 2 \cdot P R G a d v\left[\mathcal{B}, G_{B M}^{p k}\right] \]

A对KEM的bit guessing, B的k0从 PRG game 里面取，那么 \(KEMCPAadv* = PRGadv\)

ROM

有一个 random oracle \(\mathcal{O}: \mathcal{M} \rightarrow \mathcal{T}\) 类似真随机函数. 在询问里，A可以做 \(\mathcal{O}\) 询问

PRF in ROM

把 PRF 的 attack game 加入一个 random oracle 的query, Experiment 0 的时候从 RO 取

\(F_{\text {pre }}(k, x):=\mathcal{O}(k \| x)\) \[ P R F^{r o} a d v\left[\mathcal{A}, F_{p r e}\right] \leq \frac{Q_{r o}}{|\mathcal{K}|} \]

Game0里面, 用 dic 记录 ro的值，在 Game1里面舍弃dic, 只有A在 ro 里面猜到 \(k\) 才能使得这两个game不一样

Theorem 29

存在cryptographic schemes使得在ROM里secure，但是不能被securly instantiated using PPT algo

如果 \(F_{\text {pre }}(k, x):=H_{M D}(k \| x)\) 那么有attack, 对于 \(t \leftarrow F_{\text {pre }}(k, M)\)

你可以计算 \(F_{\text {pre }}\left(k, M\|p a d\| M^{\prime}\right)\) \[ h\left(M^{\prime} \| \text { pad }, t\right)=F_{\text {pre }}\left(k, M\|p a d\| M^{\prime}\right) \] 因为有prefix性质，所以A可以预先计算 \(h\) , 然后询问 \(F(M||pad||M')\) 看看是不是 \(h\)

HMAC

继承 NMAC, 但是加了 \(ipad, opad\)

image-20240723105722169

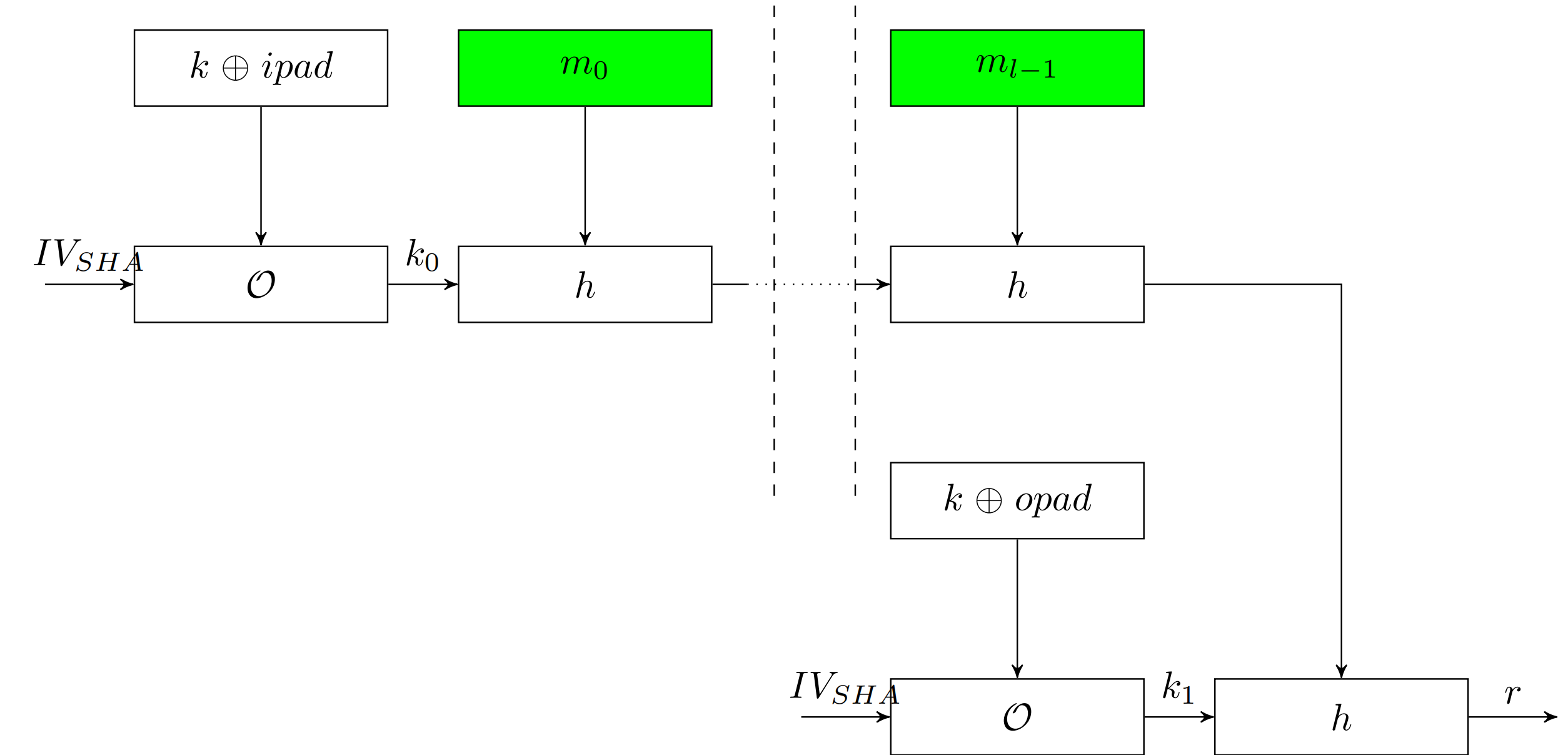
定理 30 KEM from RO

pk,sk, \(c_{k e m} \leftarrow F(p k, s)\) 然后 \(k \leftarrow \mathcal{O}(s)\) 都从 \(s\) 里生成出来 \[ K E M C P A^{r o} a d v[\mathcal{A}, \mathcal{E}] \leq O W T F a d v[\mathcal{B}, \mathcal{T}] \]

Game0 用一个dic记录RO, Game1 在生产k的时候，不记录在RO里，Game0,1的区别是，A能否猜中 \(s\) 然后向RO问 \(\mathcal{O}(s)\) , 如果这个发生，那么就可以攻击 OWTF的 attack game

RSA assumption

已知 \((l,e)\) 生成 \(l\) bit 的质数 \(p,q\) 使得 \(gcd(e,p-1)=1.gcd(e,q-1)=1\)

Let \(n=pq\) , \(d = e^{-1} \bmod lcm(p-1,q-1)\)

\(pk=(n,e),sk=(n,d)\) \[ F(p k, x):=x^e \bmod n \in \mathbb{Z}_n \text { and } I(s k, y):=y^d \in \mathbb{Z}_n \]

correctness

\(ed=1\) 因为逆元, 所以 \(ed=1+ (p-1)*k_1\) 因为 lcm一定是p-1的倍数 \[ x^{e d} \equiv x^{1+k_p(p-1)} \equiv x \cdot\left(x^{(p-1)}\right)^{k_p} \equiv x \cdot 1^{k_p} \equiv x \quad(\bmod p) \] 同理 \(x^{e d} \equiv x(\bmod q)\) 所以 \(x^{e d}-x\) 同时被p,q 整除，所以 \(x^{e d} \equiv x \quad(\bmod n)\)

RSA assumption

RSA assumption hold if \(O W T F \operatorname{adv}\left[\mathcal{A}, \mathcal{T}_{R S A}]\right.\) is negligible

Diffie-Hellman

\[ E(\alpha)^\beta=\left(g^\alpha\right)^\beta=F(\alpha, \beta)=\left(g^\beta\right)^\alpha=E(\beta)^\alpha \]

image-20240723112942018

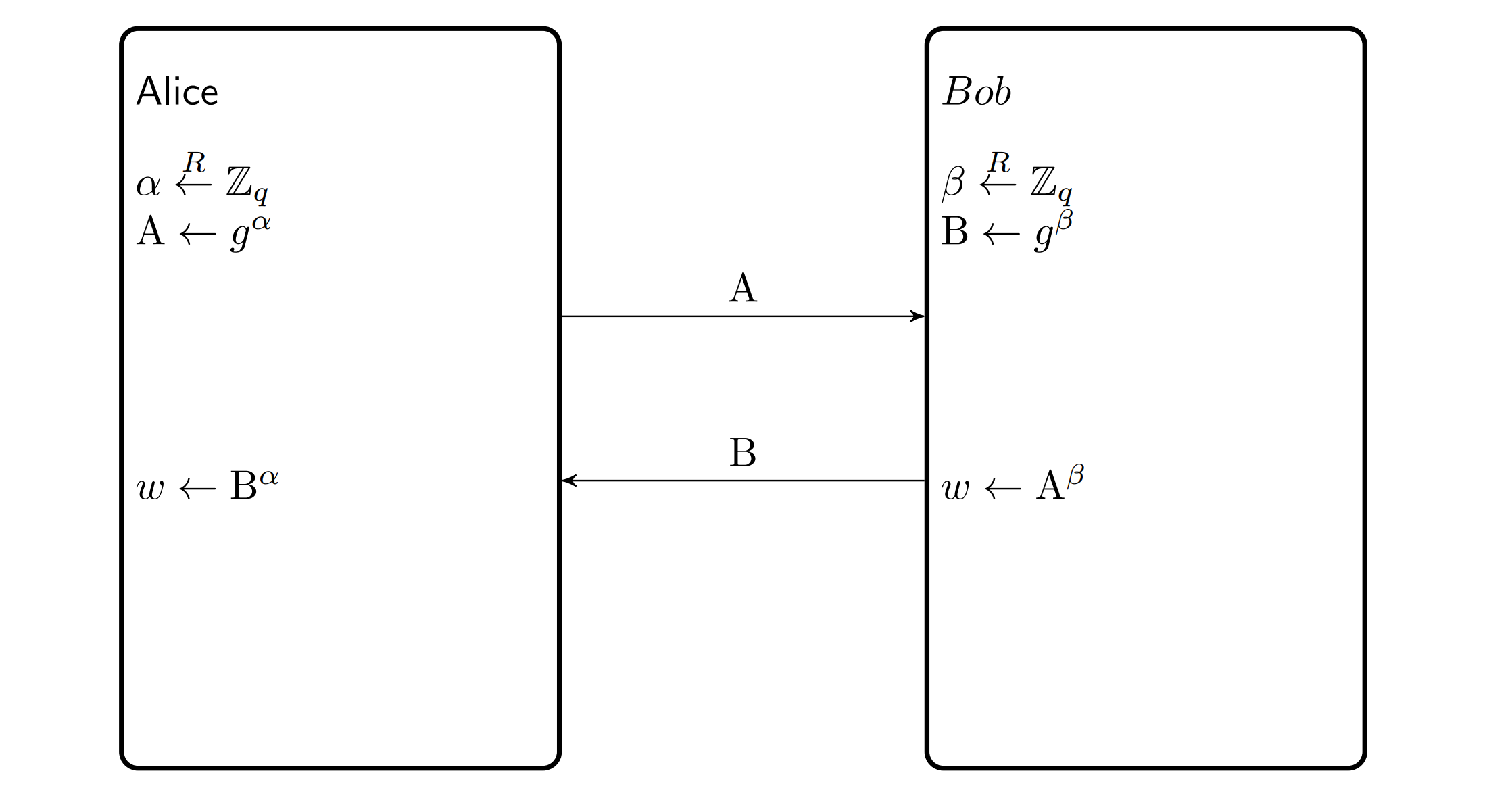
Discrete logarithm (DLOG)

\(\mathbb{G}\) 是 cyclic group, \(g\) 是generator, A 计算 \(A=g^{\alpha}\) 计算 \(\alpha\) , 定义 \(\operatorname{DLadv}[\mathcal{A}, \mathbb{G}]=\operatorname{Pr}[\hat{\alpha}=\alpha]\)

computational Diffie-Hellman assumption (CDH)

A 根据 \(\mathrm{A} \leftarrow g^\alpha, \mathrm{B} \leftarrow g^\beta\) 计算 \(w=g^{\alpha \beta}\) , \(C D H a d v[\mathcal{A}, \mathbb{G}]=\operatorname{Pr}[\hat{w}=w]\)

Diffie-Hellman KEM

\(E(pk)=(k=H(w=pk^{\beta}), g^{\beta})\) , \(D(\alpha,B)=H(B^{\alpha})\)

计算好 \(w\) 后, \(k \leftarrow H(w)\)

定理 33 DH-KEM in ROM

如果 \(H\) 是 ROM, CDH holds, 那么 \[ K E M C P A^{r o} a d v\left[\mathcal{A}, \mathcal{E}_{D H}\right] \leq Q \cdot C D H a d v\left[\mathcal{B}_{c d h}, \mathbb{G}\right] \]

和 OWTF 类似, 因为没办法验证哪一个 RO query 是 \(\hat{w}\), 那么就随机一个给CDH Attack game

decisional Diffie-Hellman (DDH)

C 计算 \(A,B,w_b\) 给 A, \(w_0=g^{\alpha \beta},w_1 = g^{\gamma}\) , \(\gamma\) 是随机数, 也是random value, 看A能否区分 \(D D H a d v[\mathcal{A}, \mathbb{G}]=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right|\)

KDF

Key derivation functions (KDFs) are used to derive cryptographically strong keys from existing keys.

AttackGame

\(x\) 是pk, 看KDF的生成key能否区分随机值

C 计算 \(x \stackrel{R}{\leftarrow} \mathcal{X}, y \stackrel{R}{\leftarrow} \mathcal{Y}, z_0 \leftarrow F(x, y), z_1 \stackrel{R}{\leftarrow} \mathcal{Z}\) ，发送 \(x,z_b\) 看是否能区分 \[ K D F a d v[\mathcal{A}, F]=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \]

HKDF

HKDF is built using the HMAC

image-20240723135637434

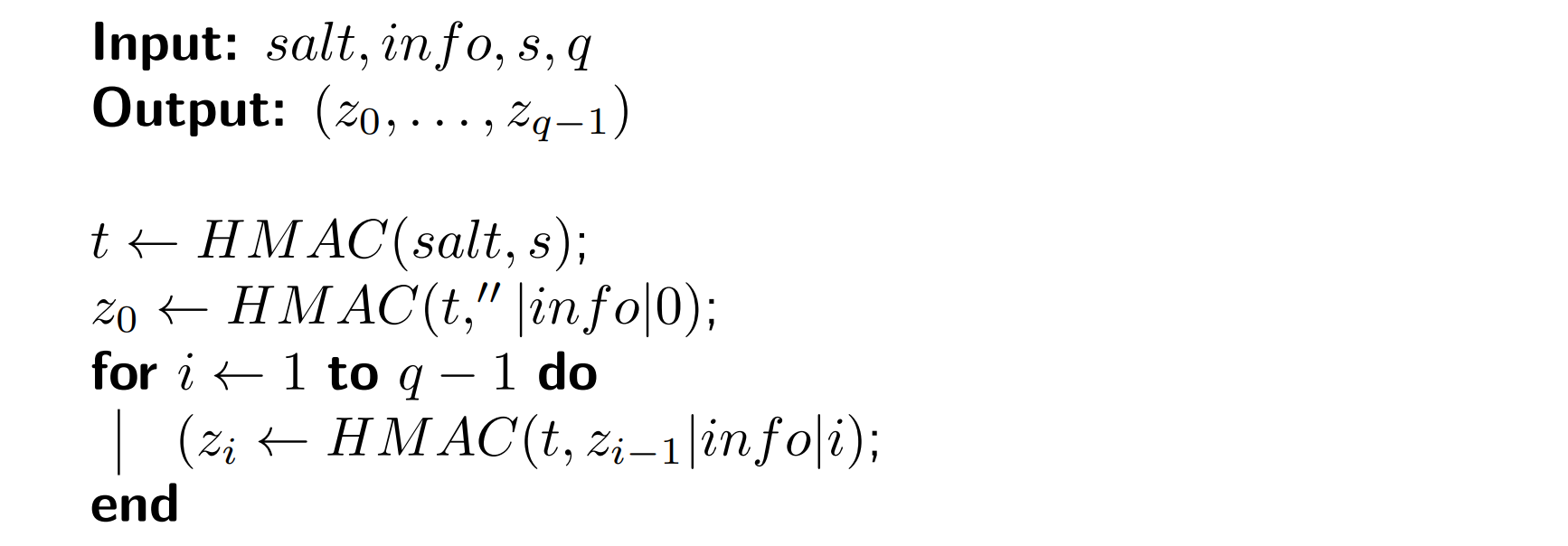
定理 35 DH KEM 是 secure

\(F\) 是 secure KDF, DDH holds, \(\mathcal{E}_{D H}\) 是 secure KEM \[ K E M C P A a d v\left[\mathcal{A}, \mathcal{E}_{D H}\right] \leq D D H a d v\left[\mathcal{B}_{d d h}, \mathbb{G}\right]+K D F a d v\left[\mathcal{B}_{k d f}, F\right] \]

直接构造就行, 先把 \(w\) 换成随机值，再把 \(k\) 换成随机值

Elliptic curves

skipped

Public Encryption Scheme

Hybrid encryption

先用 KEM 生成一个 \(k\), 然后用这个加密

Public-key encryption

\(\Pi:=(G, E, D)\) , \(G\) 生产 pk,sk, \(E,D\) 是加密解密算法，都是probabilistic 的

就是把KEM的k换成messange

PKCCA Security

C 计算 \(pk,sk\) , A 发送解密query \(c_i\), C 解密 \(m_i=D(sk,c_i)\) , 最后 A 发送2个加密，看能不能区分 \(c_0,c_1\)

定理 36

\(\Pi_s\) 是 semantically secure的，那么 \(\mathcal{E}\) 是CPA secure KEM, 那么 hybrid encryption 是 secantically secure 的 \[ P K C P A a d v[\mathcal{A}, \Pi] \leq 2 \cdot K E M C P A a d v\left[\mathcal{B}_{\text {kem }}, \mathcal{E}\right]+S C a d v\left[\mathcal{B}_s, \Pi_s\right] \]

Game0 用 KEM 生产 k, 发送 c0, Game 1随机生产k,发送c0, Game2 发送c1, Game3 KEM, 发送c1

ElGamal

\(s k:=\alpha \stackrel{R}{\leftarrow} \mathbb{Z}_q\) and \(p k:=g^\alpha\). \(k \leftarrow p k^\beta=g^{\alpha \beta}\) , \(c \leftarrow k \circ m\)

这个圆圈, G-based OTP, 就是把xor换成圆圈

CCA Security

A 可以加密，解密，最后A发送2个m, C加密其中一个，看A能否区分

KEM CCA secutiry

A可以询问 \(c_i \ne c_{kem}\) 用 \(D(sk, c_i)\) 的解密， 看A是否能区分 \(k,c_{kem}=E(pk)\) 的 \(k\) 和随机数

The CCA-secure OWTF KEM

\[ \begin{aligned} E(p k):= & x \stackrel{R}{\leftarrow} \mathcal{X}, c \leftarrow F(p k, x) \\ & k \leftarrow H(x) \end{aligned} \]

\[ \begin{aligned} D(s k, c):= & x \leftarrow I(s k, c), \\ & \text { if } F(p k, x) \neq c \text { return } \perp \\ & k \leftarrow H(x), \text { return } k \end{aligned} \]

Image oracles

对于 \(x\) 可以询问 \(F(k,x)\) 是否等于 \(y\)

OWTF with IO

C 计算 \((p k, s k) \stackrel{R}{\leftarrow} G(), x \stackrel{R}{\leftarrow} \mathcal{X}, y \leftarrow F(p k, x)\) , A 可以询问 \(y_i\) 是否合法 \(\hat{y}=F\left(p k, I\left(s k, y_i\right)\right)\), IOWadv 是 A 可以得出 \(x\) 的概率

定理 37 KEMCCA

\(\mathcal{T}\) 是OWTF, \(H\) 是 ROM \[ K E M C C A^{r o} a d v\left[\mathcal{A}, \mathcal{E}_{T D F}\right] \leq I O W a d v\left[\mathcal{B}_{\text {iow }}, \mathcal{T}\right] \]

Game0是CCA game, Game1 是不存储k在map里, Game0,1的区别是A会在ROquery里猜出x, 对于解密询问, B可以先问IO合不合法，如果合法就随机给一个. 如果A猜出来了，那么B可以赢IOW

定理 38 CCAsecure Hybrid

\(\mathcal{E}\) 是 CCAsecure KEM, \(\Pi_S\) 是 CCA secure cipher, 那么 hybrid 是CCA secure的 \[ P K C C \operatorname{Aadv}[\mathcal{A}, \Pi] \leq 2 \cdot \operatorname{KEMCCAadv}\left[\mathcal{B}_{\text {kem }}, \mathcal{E}\right]+\operatorname{CCAadv}\left[\mathcal{B}_S, \Pi_S\right] \]

\[ P K C C A^{r o} a d v\left[\mathcal{A}, \Pi_{T D F}\right] \leq 2 \cdot \operatorname{IOWadv}\left[\mathcal{B}_{\text {iow }}, \mathcal{T}\right]+\operatorname{CCAadv}\left[\mathcal{B}_S, \Pi_S\right] \]

证明与之前类似

Fujisaki-Okamoto trapdoor function

\(U\) 是一个hash function, 定义 \(E_a(p k, x ; r)\) 是随机加密函数, \(r\) 由C选择 \[ F(p k, x)=E_a(p k, x ; U(x)) \] 使得 \(\mathcal{T}_{F O}=\left(G_a, F, D_a\right)\) 安全的条件是 \(\Pi_a=\left(G_a, E_a, D_a\right)\)

• one way
• unpredictable

Unpredictable encryption

对于 \(\Pi_a=\left(G_a, E_a, D_a\right)\) 来说 对于所以 \(y\), 如果 \(r\) 随机，那么 \[ \operatorname{Pr}\left[E_a\left(p k, D_a(s k, y) ; r\right)=y\right] \leq \epsilon \]

定理 39

\(U\) 是ROM, 若 \(\Pi_a\) 是 CPA-secure 的, \(\epsilon\)- unpredictable, 那么 \(\mathcal{T}_{F O}\) 是 one-way, given an IO \[ I O W^{r o} a d v\left[\mathcal{A}, \mathcal{T}_{F O}\right] \leq Q_{i o} \cdot \epsilon+2 \cdot P K C P A a d v\left[\mathcal{B}_{c p a}, \Pi_a\right]+\frac{2 Q_{r o}+1}{|\mathcal{X}|} \]

证明难

Digital Signature

A signature scheme \(\mathcal{S}\) is

• \((s k, p k) \stackrel{R}{\leftarrow} G()\)
• 用sk签名 \(\sigma \stackrel{R}{\leftarrow} S(s k, m)\)
• 用pk验证 \(V(p k, m, \sigma)\) deterministic

Existentially unforgable (EUF)

C 计算 pk,sk, A可以向C要\(m_i\) 的签名, A伪造一个签名 \((m,\sigma)\),不可以是询问的 \(m_i\) , 使得C验证成功 \(S I G a d v[\mathcal{A}, \mathcal{S}]\)

Signature security (SUF)

和上面类似, 但是伪造的签名不可以是任何一个询问的 \((m, \sigma) \notin\left\{\left(m_0, \sigma_0\right),\left(m_1, \sigma_1\right), \ldots\right\}\) , \(\operatorname{stSIGadv}[\mathcal{A}, \mathcal{S}]\)

Full domain Hash (FDH)

用 \(H\) 先 hash message, 然后签名 \(S(s k, m):=\sigma \leftarrow I(s k, H(m))\). \[ V(p k, m, \sigma):= \begin{cases}\text { accept, } & \text { if } F(p k, \sigma)=H(m) \\ \text { reject, } & \text { otherwise }\end{cases} \]

定理 41

\((F,G,I)\) 是 OWTF, \(H\) 是 ROM, 那么 \[ S I G^{r o} a d v\left[\mathcal{A}, \mathcal{S}_{F D H}\right] \leq\left(Q_{r o}+1\right) \cdot O W T F a d v[\mathcal{B}, \mathcal{T}] \]

不妨假设A会询问 \((\hat{m},\hat{\sigma})\) 的 RO query. 那么我们把 OWTF 给的 \(y\) 在其中的一个RO query里面回复. 那么就有概率, A给出的伪造是我们需要的

(strongly )q-time signature

A最多询问 \(q\) 次

Lamport signature

首先有pk和 sk \[ s k:=\binom{x_{0,0}, \ldots, x_{v-1,0}}{x_{0,1}, \ldots, x_{v-1,1}} \stackrel{R}{\leftarrow} \mathcal{X}^{2 v} \text { and } p k:=\binom{y_{0,0}, \ldots, y_{v-1,0}}{y_{0,1}, \ldots, y_{v-1,1}} \in \mathcal{Y}^{2 v} \]

\[ S\left(s k, m=\left(m_0, \ldots, m_{v-1}\right)\right):=\left(x_{0, m_0}, \ldots, x_{v-1, m_{v-1}}\right)=\sigma \in \mathcal{Y}^v \]

更广义 \[ \begin{aligned} s k & \stackrel{R}{\leftarrow} \mathcal{K} \\ \left(x_0, \ldots, x_{n-1}\right) & :=(F(s k, 0), \ldots, F(s k, n-1)) \\ p k & :=\left(y_0, \ldots, y_{n-1}\right)=\left(f\left(x_0\right), \ldots, f\left(x_{n-1}\right)\right) . \end{aligned} \] \(p(m)\) 可以把一个 \(m\) 映射到 \(\{0, \ldots, n-1\}\) 的子集上 \[ V\left(p k, m,\left(\sigma_0, \ldots, \sigma_u\right)\right)= \begin{cases}\text { accept } & \text { if } l=u \text { and } \forall i \in\{0, \ldots, l-1\}: f\left(\sigma_i\right)=y_{s_i} \\ \text { reject } & \text { otherwise. }\end{cases} \]

containment free

对于所有 \(m,m'\), \(P(m)\) 不被 \(P(m')\) 包含

定理 42

\(F\) 是 PRF, \(f\) 是 one-way fuction, \(P\) 是 containment free function, 那么这个是 secure one-time signature \[ \operatorname{SIGadv}\left[\mathcal{A}, \mathcal{S}_P\right] \leq n \cdot O W F a d v\left[\mathcal{B}_f, f\right]+P R F a d v\left[\mathcal{B}_F, F\right] \]

先把 \(F\) 换成 \(f\), 然后对于 OWF 的询问，替换掉一个随机的 \(y_i\),不妨假设被替换的没有被发现, 然后对于伪造有 \(1/n\) 的概率宣导我们替换的

对于 SPR 的 \(f\) \[ \begin{aligned} \operatorname{stSIGadv}\left[\mathcal{A}, \mathcal{S}_P\right] & \leq n \cdot\left(O W F a d v\left[\mathcal{B}_{O W}, f\right]+\operatorname{SPRadv}\left[\mathcal{B}_{S P R}, f\right]\right)+P R F a d v\left[\mathcal{B}_F, F\right] \\ & \leq S I G a d v\left[\mathcal{B}_{S I G}, \mathcal{S}_P\right]+n \cdot S P R a d v\left[\mathcal{B}_{S P R}, f\right] . \end{aligned} \]

证明在上面的最后一步，如果A给的 \(m\) 和query一样, 那么存在second preimage, 有\(1/n\) 的概率宣导我们替换的，否则就可能赢OWF

Strongly secure hybrid signatures

\(\mathcal{S}_{\infty}=\left(G_{\infty}, S_{\infty}, V_{\infty}\right)\) 是可以多次签名的, \(\mathcal{S}_1=\left(G_1, S_1, V_1\right)\) 是只能签1次的

先前 public key, 然后用 S1 签名 \[ \begin{aligned} S\left(s k_{\infty}, m\right):= & \left(p k_1, s k_1\right) \stackrel{R}{\leftarrow} G_1() \\ & \sigma_{\infty} \stackrel{R}{\leftarrow} S_{\infty}\left(s k_{\infty}, p k_1\right) \\ & \sigma_1 \stackrel{R}{\leftarrow} S_1\left(s k_1,\left(m, \sigma_{\infty}\right)\right) \\ & \text { output } \sigma:=\left(p k_1, \sigma_{\infty}, \sigma_1\right) \end{aligned} \] 验证的时候先验证pk1, 然后再验证 \[ \begin{aligned} V\left(p k_{\infty}, m, \sigma\right):= & \text { output reject if accept } \neq V_{\infty}\left(p k_{\infty}, p k_1, \sigma_{\infty}\right) \\ & \text { output reject if accept } \neq V_1\left(p k_1,\left(m, \sigma_{\infty}\right), \sigma_1\right) \\ & \text { output accept } \end{aligned} \]

定理 43

若 \(S_{\infty}\) many time secure 和 \(S_1\) 是 one-time strongly secure, 那么 hybrid 是 strongly secure的 \[ \operatorname{stSIGadv}[\mathcal{A}, \mathcal{S}] \leq Q_s \cdot \operatorname{stSIGadv}\left[\mathcal{B}_1, \mathcal{S}_1\right]+\operatorname{SIGadv}\left[\mathcal{B}_{\infty}, \mathcal{S}_{\infty}\right] \]

\(\left(\hat{m},\left(\hat{p k}_1, \hat{\sigma}_{\infty}, \hat{\sigma}_1\right)\right)\) 是伪造的签名, 如果 \(\hat{pk_1}\) 出现过, 那么我们可以把一个query替换成 one-time给的, 然后 \(1/Q\) 的概率选到. 如果 \(\hat{pk_1}\) 没有出现过, 那么是一个 many time 的一个伪造

Authenticated Key Exchange

证书由第三方签名 \[ \operatorname{Cert}_{i d}:=\left(\left(i d, p k_{i d}\right), \sigma_{i d, p k_{i d}}\right) \]

attack game

C 有所有 honest instances 的信息

A 有所有 vulnerable 的信息

A 可以选择场景, 可以询问一个某一个到达的信息, C要返回这个回答和status

\(status=\)

• \(running\)
• \(abort\)
• \((finish, pid, k)\) k 是使用的session key

Experiment 0 里面, C 在status里回答session key

image-20240724233703957

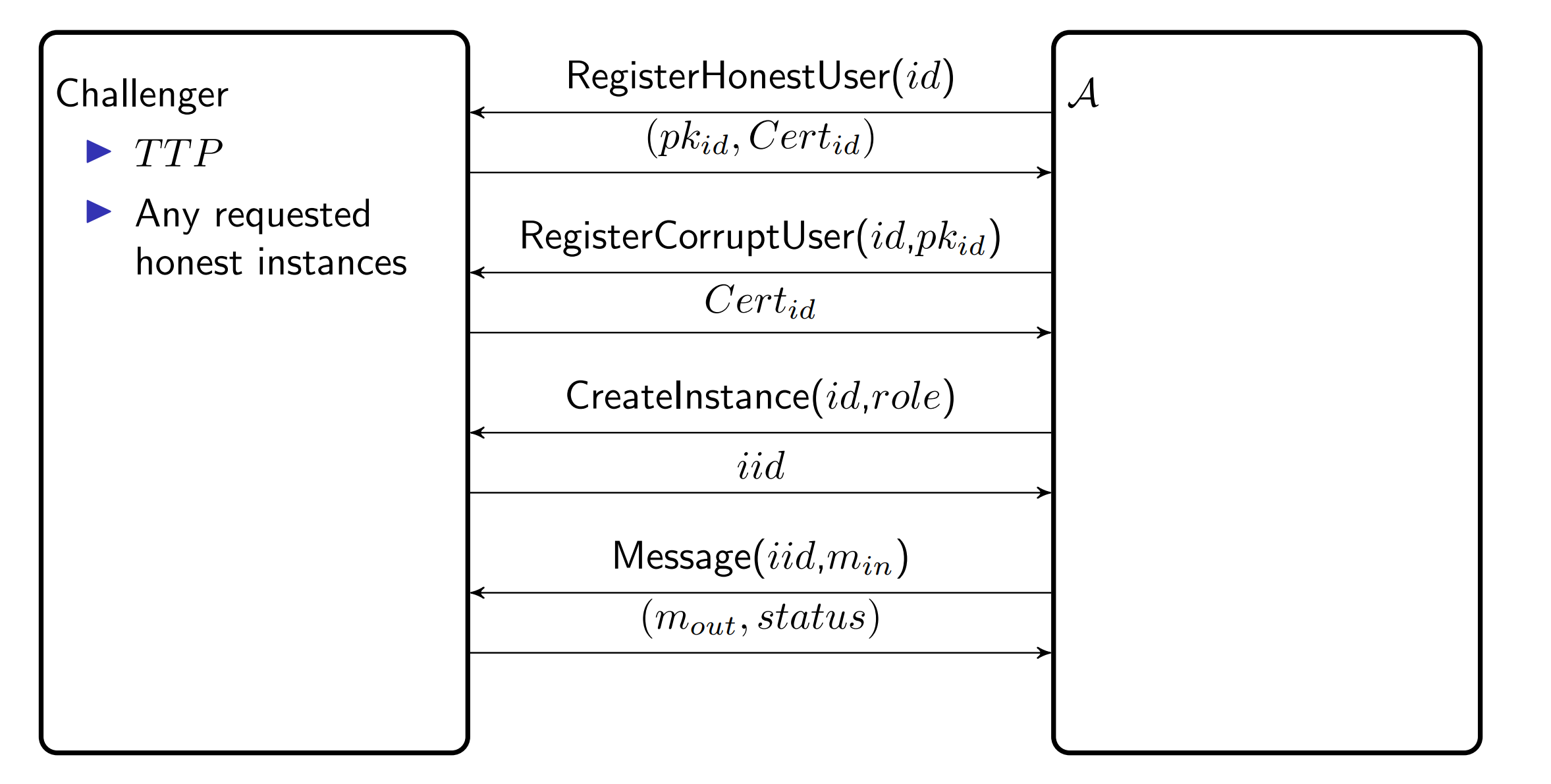
Experiment 1

我们有一个 partner function 来定义发送信息的对方的类型

• \(fresh\) 新的连接，返回随机k，如果对方是honest
• \(connected \ to \ J\) 回答对应的key 如果 \(J\) 是对应的
• \(vulnerable\) 回复对应的key ( 因为 A control 所有 vulnerable)

Statically Secure AKE

使得 A 无法区分这两个实验 \[ s A K E a d v[\mathcal{A}, \mathcal{P}, p f]=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \]

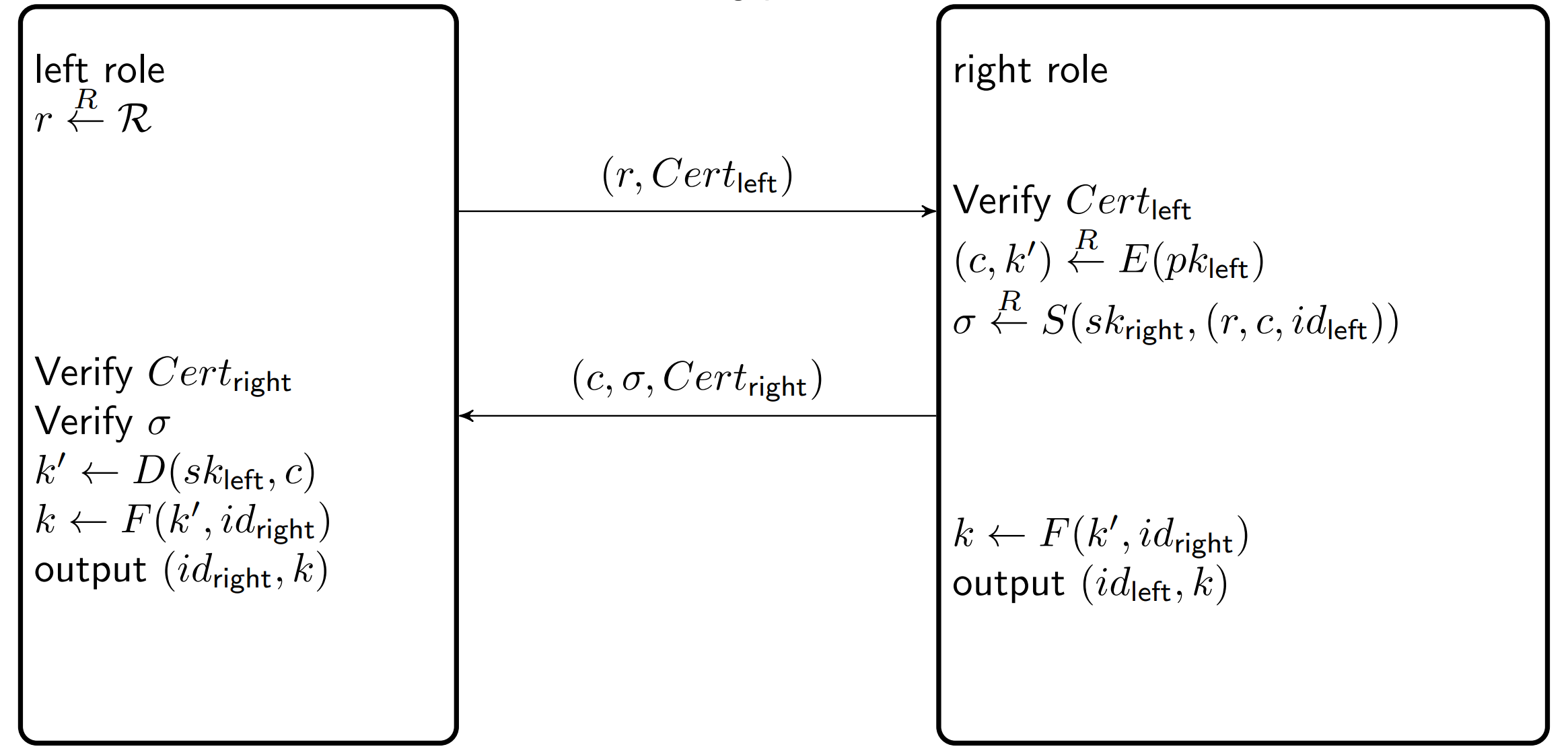
定理 44

\(\mathcal{S}=\left(G_{\mathcal{S}}, S, V\right)\) 是secure signature scheme\(\mathcal{E}=\left(G_{\mathcal{E}}, E, D\right)\) 是 CCA secure KEM, \(F\) 是secure PRF 下面的是static secure的

\[ \begin{aligned} s A K E a d v^*[\mathcal{A}, \mathcal{P}, p f] &\leq N_{h u} \cdot \operatorname{SIGadv}[B, \mathcal{S}] \\ & +\frac{N_{l i}^2}{2|\mathcal{R}|}+\frac{N_{r i}^2}{2|\mathcal{K}|} \\ & +N_{r i} \cdot(K E M C C A a d v[C, \mathcal{E}]+P R F a d v[D, F]) \\ & \end{aligned} \] 证明

Game0: 对应sAKE的bit guessing game

Game1: 在left Verify signature的时候，除了检查Verify Algorithm, 还检查对应的honest instance 有没有签名 \[ \left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \leq N_{h u} \cdot S I G a d v[B, \mathcal{S}] \] Game2: \(r\) 不能重复, \(\left|\operatorname{Pr}\left[W_1\right]-\operatorname{Pr}\left[W_2\right]\right| \leq \frac{N_{l i}^2}{2|\mathcal{R}|}\)

Game3 \(c\) 不能重复 \(\left|\operatorname{Pr}\left[W_2\right]-\operatorname{Pr}\left[W_3\right]\right| \leq \frac{N_{r i}^2}{2|\mathcal{K}|}\)

Game4, 在 \(c\) 传输的过程中, 改成另一个 \(k*\) , 到了之后再改回来 (因为C控制所有honest) \[ \left|\operatorname{Pr}\left[W_3\right]-\operatorname{Pr}\left[W_4\right]\right| \leq N_{r i} \cdot K E M C C A a d v[C, \mathcal{E}] \] Game5, 把 \(F\) 改成 \(f\) \[ \left|\operatorname{Pr}\left[W_4\right]-\operatorname{Pr}\left[W_5\right]\right| \leq N_{r i} \cdot \operatorname{PRFadv}[D, F] \] 这样在 fresh中随机输出的时候，就和随机没区别了, A只能猜

PFS

perfect forward secrecy: 就是在被得知 \(sk\) 后, 之前传输的信息还能保持安全.

我们每次用一个新的pk来传输

image-20240725091227027

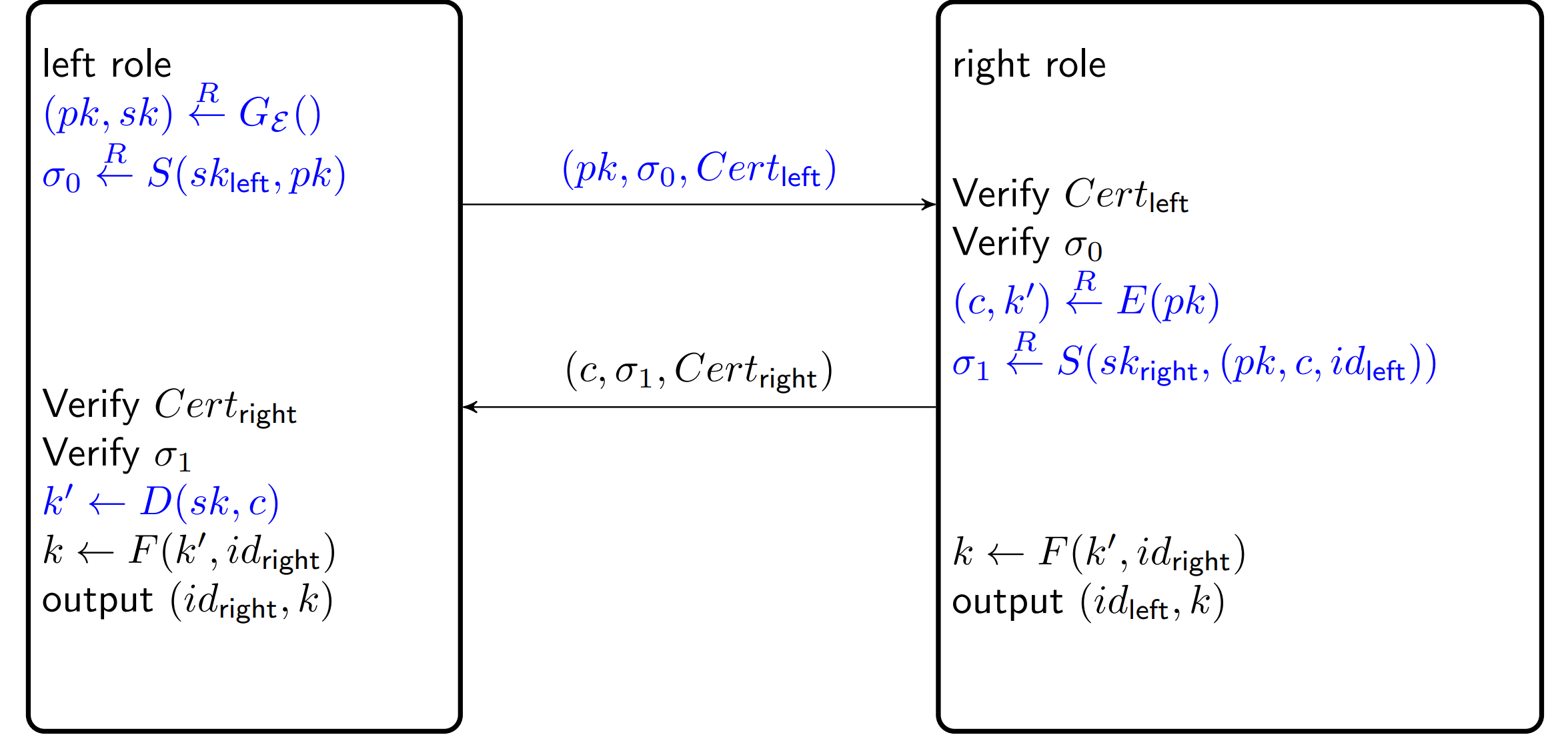
HSM Secure AKE

Hardware secure module 可以被 attacker 使用

这样 Attacker 可以预先生产很多keypair来用作以后的impersonation

image-20240725092346986

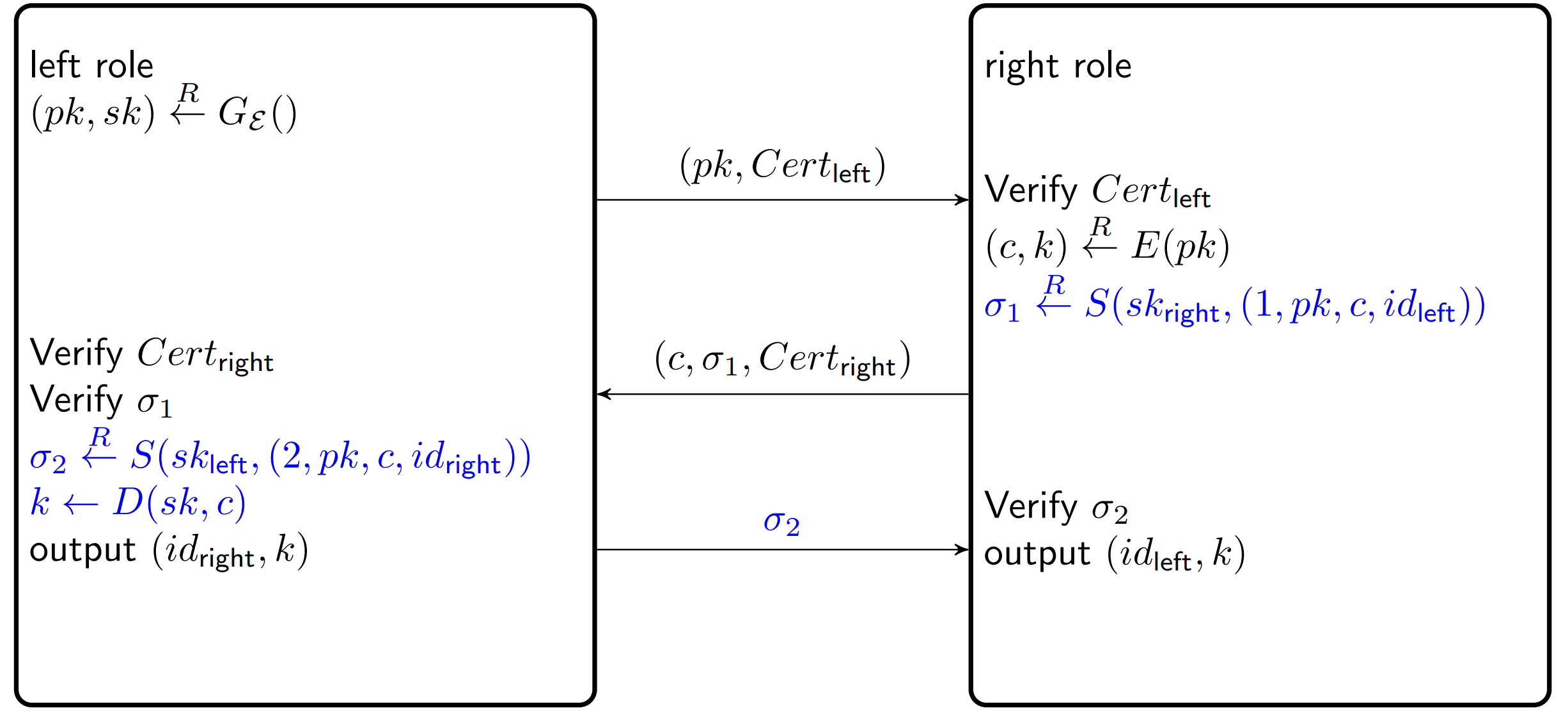
解决方法是不预先签名，只有产生交互了再签名

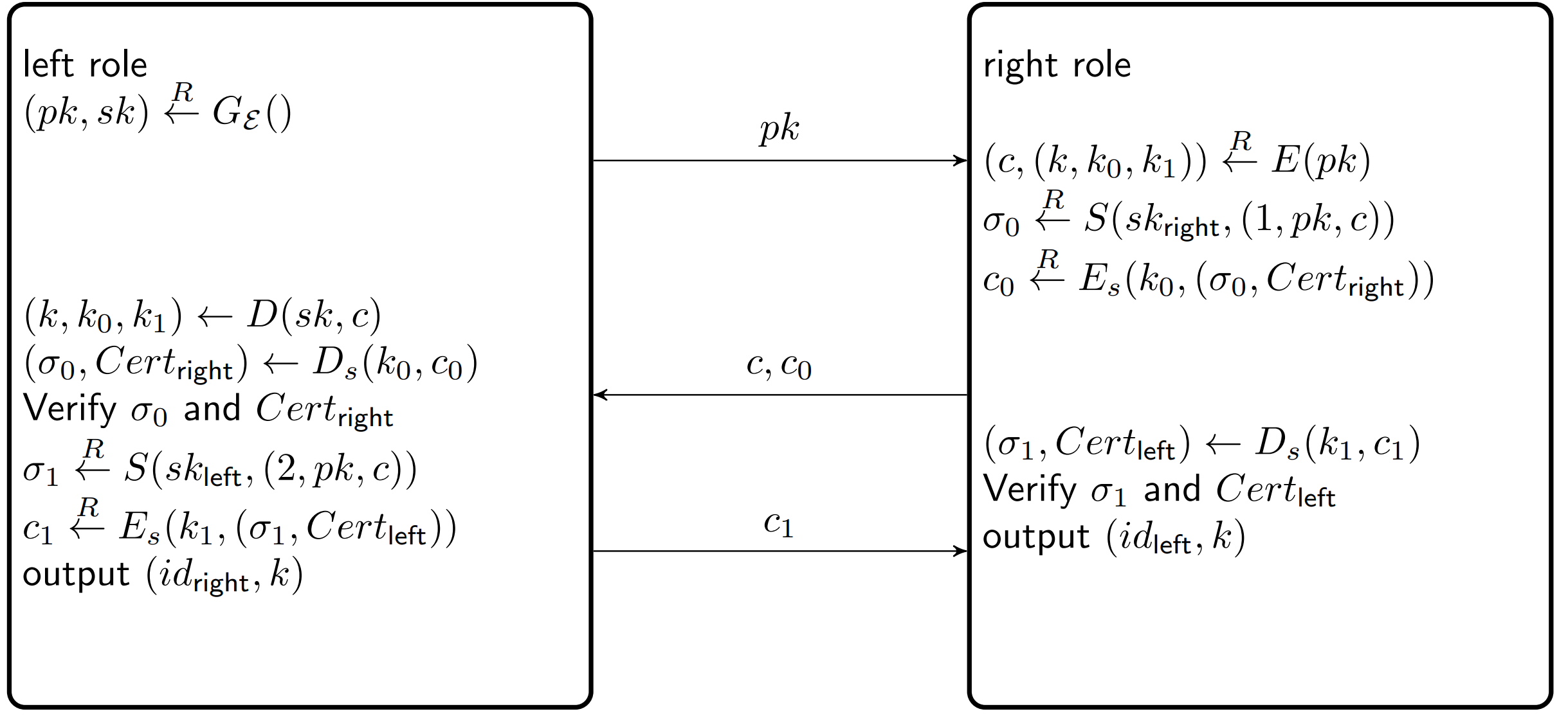
Baby-TLS

额外有 identity protection的性质, Certificate 也进行加密

image-20240725092800128

Exercise

2.1 Computational indistinguishable

\(S_n\) 是集合的数列, \(D_n^{1}\) ,\(D_{n}^2\) 是2个在 \(S_n\) 上概率分布的数列, 定义等关系 \(\stackrel{c}{\equiv}\) 这两个 computationally indistinguishable, \(\epsilon(n)\) 是 negligible 函数. \(S=\{0,1\}\) \[ \left|\operatorname{Pr}\left[A\left(D_n^1\right)=1\right]-\operatorname{Pr}\left[A\left(D_n^2\right)=1\right]\right| \leq \epsilon(n) \]

定义的解释

• \(n\) 是长度的函数, 比如 \(S_n = \{0,1\}^{l(n)}\) ,\(\ell(n)=n^{O(1)}\)

  \(S_5=\{0,1\}^5\) 是所有长度为 \(5\) 的 01 串的集合, \(D_5\) 就是在 \(S_5\) 上的概率分布, 描述每个字符串出现的概率

• 这样的数列就包含了所有长度的01串

4.2 CCA2

\(\Pi=(E, D)\) 是 CCA2的, \(\mathcal{I}=(S, V)\) 是 EUF-CMA 的 MAC, 证明下面的是 AE \[ E^{\prime}\left(\left(k_1, k_2\right), m\right):=t \stackrel{R}{\leftarrow} S\left(k_1, m\right) \text {; return } E\left(k_2,(m, t)\right) \]

\[ D^{\prime}\left(\left(k_1, k_2\right), c\right):=(m, t) \leftarrow D\left(k_2, c\right) \text {; if accept }=V\left(k_1, m, t\right) \text { then return } m \text { else return } \perp \]

证明：

不能直接构造，因为 A 返回的\(c\) 有可能是 \(m=m_i\) 就不符合 EUF 的定义

要证明AE，可以先证明CPA secure，再证明CI secure

CPA secure: 可以用 A 直接构造一个B攻击\(\Pi\) 的 CPA \[ C P \operatorname{Aadv}\left[A, \Pi^{\prime}\right] \leq C C \operatorname{Aad} v\left[A, \Pi^{\prime}\right] \leq \operatorname{CCAadv}[B, \Pi] \] CI secure：

• Game 0: \(\Pi '\) 的 CI game
• Game i: 前 \(i\) 个 \(m_i\) 正常加 tag, 后面的 \(m_i\) 用随机数加tag

可以转移到 \(\Pi\) 的 CCA game 上，把第 \(i\) 个game的tag，和一个随机生产的tag，扔给 \(\Pi\) 的 \(m_0,m_1\)

如果 A win CI Game，那么 B 对 \(\Pi\) 发送 1

这样 \(\Pi\) 的 Exp0 对应 Game i, Exp 1 对应 Game i-1

所以 \(\left|\operatorname{Pr}\left[W_i\right]-\operatorname{Pr}\left[W_{i+1}\right]\right| \leq CCAadv[B,\Pi]\)

• Game Q: 所有tag 是随机的, \(\text{Pr}[W_Q]\) 的概率A给出一个 \(c\), 那么就有了一个伪造, 可以直接赢 EUFMACadv

\[ Pr[W_0]-Pr[W_Q] \le |Pr[W_0] - Pr[W_Q]| \le \sum_{i=0}^{Q-1}|Pr[W_i]-Pr[W_{i+1}]| \\ CIadv[A,\Pi'] \leq Q \cdot C C A a d v[B, \Pi]+E U F M A C a d v[C, \mathcal{I}] \]

4.3

\(S_{\text {det }}\left(k,\left(m_0, \ldots, m_{d-1}\right), r\right):=\) for \(i\) in \([d]\) do \(t_i \leftarrow F_k\left(\left(r, i, d, m_i\right)\right)\) done; return \(\left(t_0, \cdots, t_{d-1}\right)\) \[ S(k, m):=r \stackrel{R}{\leftarrow}\{0,1\}^n ; \operatorname{return}\left(r, S_{\text {det }}(k, m, r)\right) \] \(V(k, m,(r, t)):=\) if \(t=S_{\mathrm{det}}(k, m, r)\) then return accept else return reject

证明 这个MAC 安全

首先可以把 \(F\) 换成 \(f\)

剩下有两种情况

• \(r\) 有出现过2次，那么可以直接构造forgery, 组合他们的一部分
• \(r\) 都不同, 那么改动最后一个, 猜测最后一个 \(f\) 的output即可 (讨论A必须猜)

\[ \operatorname{MACadv}[A, \mathcal{I}]:=\operatorname{Pr}\left[W_0\right] \leq\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right|+\operatorname{Pr}\left[W_1\right] \leq \text { PRFadv }[B, F]+\frac{Q^2}{2 \cdot 2^n}+\frac{1}{2^n} \]

Zyklische Gruppe

Group

集合 \(G\) ,一个映射 \(G \times G \rightarrow G\) ,\((\sigma, \tau) \mapsto \sigma \cdot \tau\) 满足

• 交换律 \(\forall \sigma, \tau, \rho \in G: \quad(\sigma \cdot \tau) \cdot \rho=\sigma \cdot(\tau \cdot \rho)\)
• 存在左单位元 \(\exists \iota \in G: \quad \forall \sigma \in G: \quad \iota \cdot \sigma=\sigma\)
• 存在左逆元 \(\forall \sigma \in G: \quad \exists \sigma^{\prime} \in G: \quad \sigma^{\prime} \cdot \sigma=\iota\)

commutative group (abelsch)

若额外满足交换律

\(\forall \sigma, \tau \in G: \quad \sigma \cdot \tau=\tau \cdot \sigma\).

整数集合

\(\mathbb{Z}_N:=\{0,1,2, \ldots, N-1\}\)

和 \(N\) 互质系

\[ \mathbb{Z}_N^*:=\left\{k \in \mathbb{Z}_N \mid \operatorname{ggT}(k, N)=1\right\} \]

\(\mathbb{Z}_{15}^*=\{1,2,4,7,8,11,13,14\}\)

素数

\(\mathbb{P}=\{p \in \mathbb{N}|p>1 \wedge \forall n \in \mathbb{N}: n| p \rightarrow(n=1 \vee n=p)\}=\{2,3,5,7,11,13, \ldots\}\)

欧拉函数

\[ \varphi(N):=\left|\mathbb{Z}_N^*\right| \]

求欧拉函数 \[ \varphi(N)=\left|\mathbb{Z}_N^*\right|=N \prod_{p \in \mathbb{P}: p \mid N}\left(1-p^{-1}\right) \] \(\varphi(15)=15\left(1-\frac{1}{5}\right)\left(1-\frac{1}{3}\right)=(5-1)(3-1)=8\).

枚举所有质因子

Generator

\[ \langle a\rangle:=\left\{a^k \mid k \in \mathbb{Z}\right\}=\left\{\ldots,\left(a^{-1}\right)^3,\left(a^{-1}\right)^2, a^{-1}, 1, a, a^2, a^3, \ldots\right\} \]

Ordnung

\[ \operatorname{ord}(a):=\min \left\{k \in \mathbb{N} \mid a^k=1\right\} \]

定理

• \(a^k=a^{k \bmod \text { ord(a) }}\)
• \(\langle a\rangle=\left\{1, a, a^2, \ldots, a^{\text {ord }(a)-1}\right\}\)
• \(|\langle a\rangle|=\operatorname{ord}(a)\)

cyclic group

if exists a generator \(\langle a\rangle=\mathbb{G}\)

• Jede zyklische Gruppe ist kommutativ

generators

\(N:=|\mathbb{G}|\) ,\(\langle a\rangle=\mathbb{G}\) 当且仅当 \(\forall p \in\{p \in \mathbb{P}: p \mid N\}: a^{N / p} \neq 1\)

\(Z_n\) 有 \(\phi(n)\) 个 generator.

Additional

理解构造

说一说secret key crypto 和 public key crypto都有哪些组件，分别可以用什么实现

Questions

CCA为啥要PRP，

PRP好证明性质

为啥这个就CCAsecure了，之前就不行

之前的不一定不行

为啥要考虑 r 相同的事情:

因为，可以用 Encryption来得到C，看看这个c和c_hat 是不是一样来区分

Luby-Rackoff Proof 有collision会怎么样

Sn eine Folge von Mengen 为啥 是 Mengen 的 Folgen

S.211 PRP and PRF implementation equal?

只说了 Experiment 0 是相同的，都是一个函数 \(F(k,\cdot)\)

S. 225 证明错误？应该是在 \(Z\) 的情况下

\(Z\) 是reject, 和不在map里不一样，是因为CI，decryption自带的reject

为啥要Prefix-free, 证明里似乎没用到

证明里用到了，否则A可以像那样预测一个新的值，就不是随机的了

为什么 H is cr => H is 2nd preimage resistant => H is oneway

因为如果不SPR，那么可以构造一个collision

为啥 constructing a PRF from MD hash functions is problematic.

为啥RSA： ed ≡ 1 + kp(p − 1) for some integer kp. （356）

为啥 a deterministic encryption scheme cannot be CPA secure.

为啥 KDFadv=0 403

因为 F(x,y)=y 了之后，y就是一个随机数，随机数和随机数无法区分

Typo 403k-1c, 384ro, 393下标

为啥PKCCA的定义里没有PIs

Sig adv 和 stSIG adv 区别

一个是strong