Week1 : 树

概念

  • vollständige Baum 完全树(所有节点有相同孩子个数)

  • -verzweigte Baum k叉树

数学归纳法

证明完全二叉树的深度为

Induktionsanfang:

==n = 1==: Laut induktiver Definition enthält jeder Unterbuam mindestens einen Knoten. n=1 bedeutet also, dass der Baum ein Blatt ist. Die Tiefe ist 1. Zu zeigen ist also: . Es gilt

Induktionsvoraussetzung:

==Für alle gilt, dass== die Tiefe eines s vollständigen 2-verzweigten Baumes mit Knoten höchstens ist.

Induktionsschritt:

==Betrachte Bäume mit Knoten.== Fallunterscheidung:

  1. Es existiert ein mit . Weil der Baum , also mindestens zwei Knoten besitzt, kann er kein Blatt sein. Es gibt also Unterbäume, die jeweils höchstens n Knoten besitzen, da ein innerer Knoten schon vergeben ist. Laut IV ist die Tiefe der Unterbäume jeweils höchstens . Da die Tiefe kleiner als und eine ganze Zahl ist, kann sie höchstens sein. Damit ist die Tiefe des gesamten Baumes höchstens , was zu zeigen war.

  2. Es existiert kein mitt . Dann gibt es auch keinen vollständigen 2-verzweigten Baum mit Knoten, und es ist nichts zu zeigen. Dass es zu allen vollst¨andigen 2-verzweigten Bäumen ein k gibt, so dass die Zahl der Knoten ist, kann man mittels Induktion nach der Tiefe t des Baumes zeigen. Für gilt , fur einen vollständigen 2-verzweigten Baum der Tiefe t+1 gibt es dann nach IV ein entsprechendes k fur die Unterbäume der Tiefe t, und weil die Unterbäume gemäß Definition gleich sind, ist das k ebenfalls gleich, d.h. die Gesamtzahl der Knoten ist

Week 2 复杂度

公式

组合数放缩: 二项式定理: 倒着加和不编:

重要结论

阶乘放缩

Asymptotische Notation

  • 增长不比 快

  • 增长不必 慢

  • 与 增长相同

  • 比 增长慢

  • 比 增长快

运算性质

  • 交换性质

  • 传递性

Week 3

求期望运行时间

把每一种情况出现的概率用期望加起来

求平均复杂度

把所有情况的复杂度加起来取平均值

image-20200728104445205

是每一种情况运行的时间， 是每一种情况出现的概率. 加权加起来就是了

Week 4

均摊分析 - 账本方法

是一个操作 的实际运行时间. 所有有一个序列 的操作运行时间

定义函数 有如下的性质

  • 对于所有操作序列
  • 尽可能好

这个函数是账户的数目变换，若 那么账户收入，如果 那么账户支出. 是均摊运行时间.

于是一个序列的均摊时间是

Week 6

Universelles Hashing

主定理 Master Theorem

且 . 考虑递归式

  • Case 1: ,
  • Case 2: ,
  • Case 3: , 且对于足够大的 和 满足 ,

Week 9 堆

二叉堆

操作

  • build构造

    把数组依次按顺序填入二叉树(从上到下，从左到右). 然后自底向上shiftdown()调整

  • insert

    把数字插入到二叉树最后一个位置，然后自底向上 shiftdown()

  • deleteMin

    把最小值和最后一个位置交换，删除，然后对首元素 shiftdown()

  • decreaseKey

    减小之后shiftUp

  • delete

    和最后一个元素交换删除，然后shiftUp,然后shiftdown

二项堆

操作

  • insert

    直接加在链表上

  • deleteMin

    删掉最小的，然后merge

  • merge

    先加到链表上，然后从小到大按rank合并

性质

  • Rang = Tiefe =

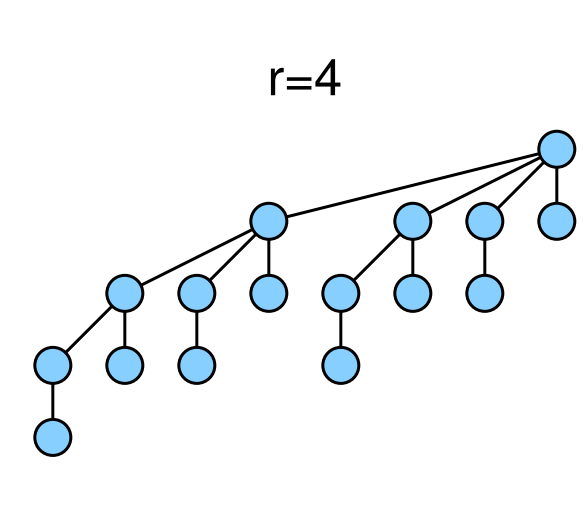
    image-20200730152520752

  • 第 深度有 个节点

  • 总节点个数

复杂度

image-20200730152901077

Week 10 AVL 树

AVL 树

选择

  • 左旋

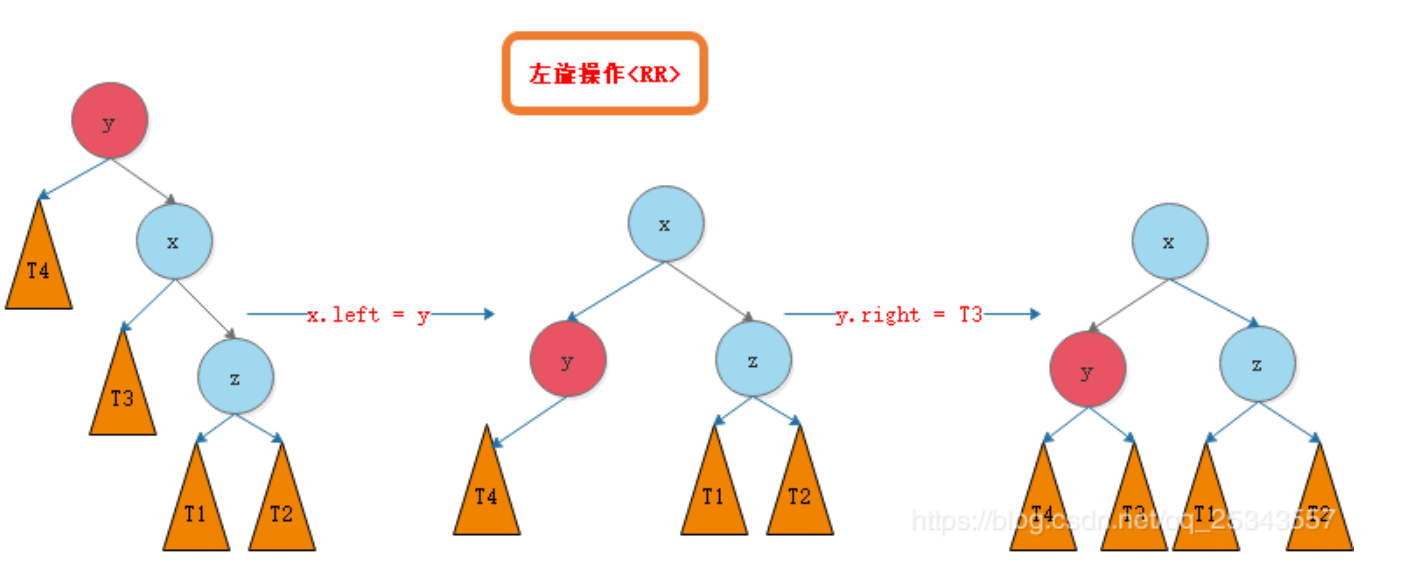
    image-20200731114320309

  • 右旋

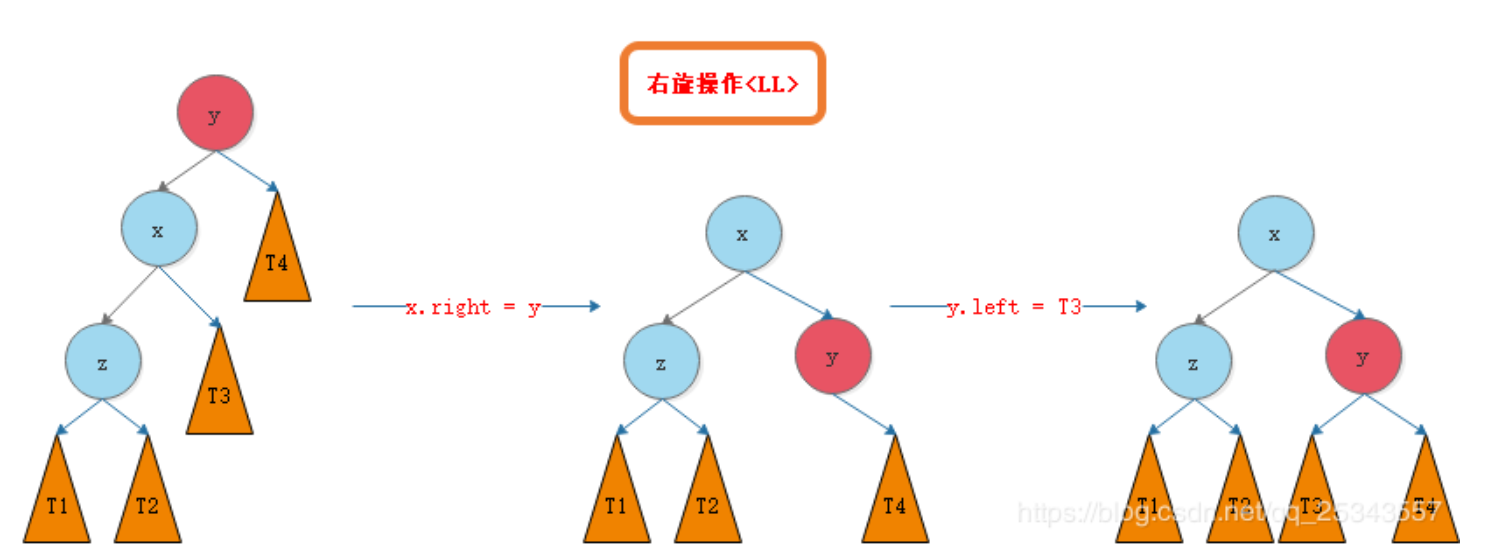
    image-20200731114349958

  • 左右旋

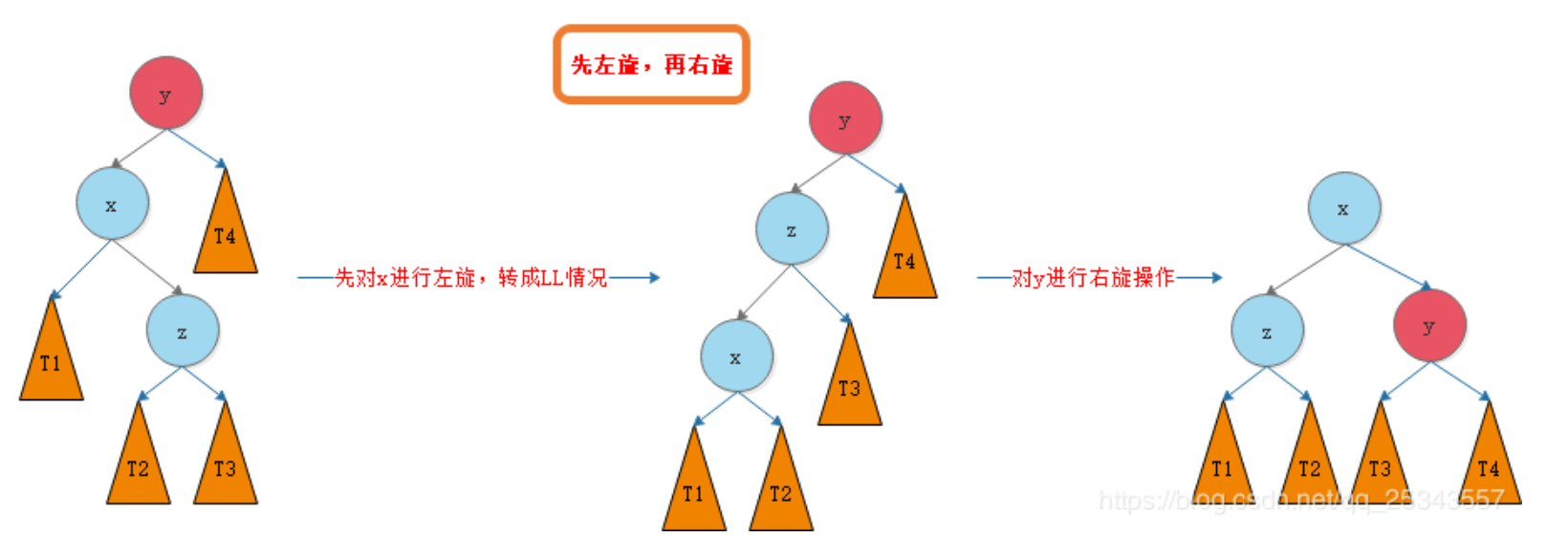
    image-20200731114431467

  • 右左旋

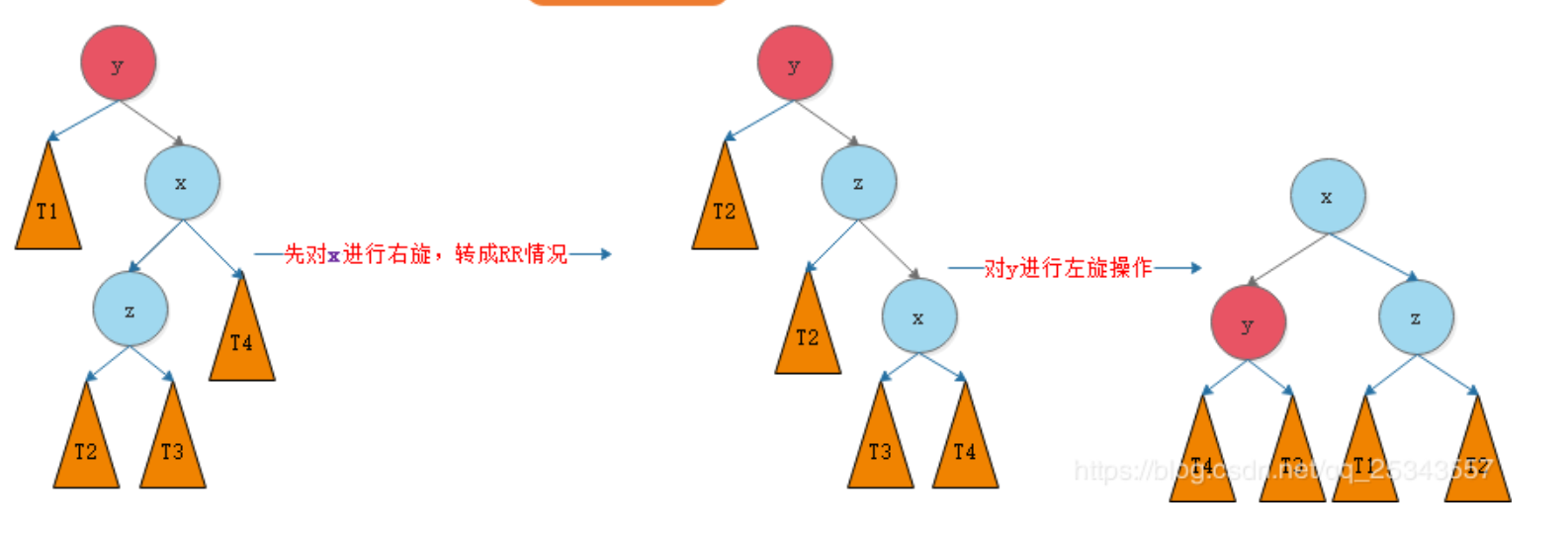
    image-20200731114456910

操作

  • 插入

    找到对应的位置插入，然后回溯的时候旋转

  • 删除

    把那个元素和它的前驱交换，然后删除前驱。然后旋转

(a,b) 树

  • 插入

    找到对应位置，然后插入. 如果儿子多了，就把中间的部分像父亲推，然后其余部分拆成2个节点

  • 删除

    先看左右兄弟能不能借儿子，如果不能就和左右的某一个合并