编译原理 | Fyind's Blog

语义分析

大观念是输入一个程序文本，我们把它分解为一个个小的词组(Token)

Token

名字 ,
常数 ,
操作符
保留字

Siever

在做分析之前，我们要进行预处理(pre-processing):

扔掉多余的：空格，注释
收集Pragmas,
用它们更具体的含义代替 Token，比如constants,names

正则表达式

时程序编写的有限字符集

定义：正则表达式的集合时最小的集合，满足：

($$ 不是中的新符号)
对于所有
, 若

练习 1.1 根据要求写出正则表达式

我们定义了一个语法：

对于 ,我们递归地定义一个语言如下： > 练习1.2 写出正则表达式的语言

对于一个正则表达式，我们也有一棵树与之对应：

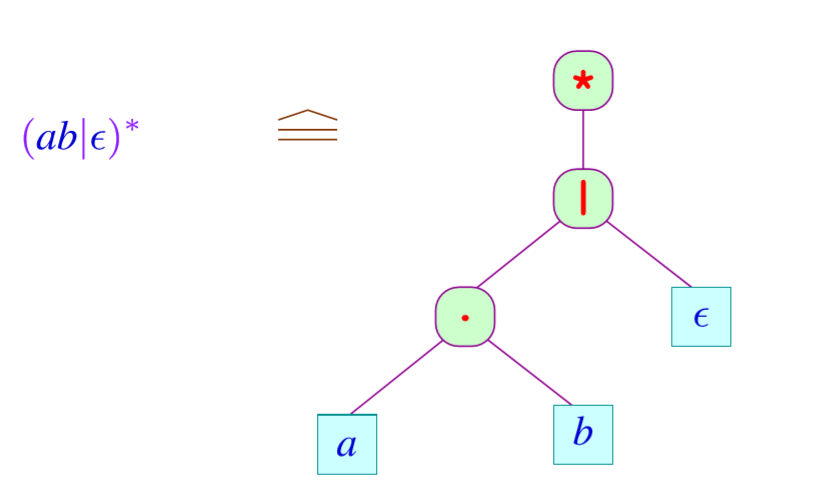
有穷自动机

一个不确定的有穷自动机( nicht-deterministischer endlicher Automat (NFA) ) 是一个元组 .

是事件的有限集
是有限的字符集
是初始状态集合
是结束状态集合
是转移关系

若是一个函数，且(只有一个初始状态)，那么它是确定的有穷自动机

transitiven Abschluss(传递闭包)

传递闭包是最小的集合满足：

若，

传递闭包描述了对于任意两个状态，它们怎么从一个到另一个。

可接受语言

一个自动机的可接受语言是：

从表达式转换到NFA

Thompson’s 算法

下面的式子可以这么转换,处理长度的正则表达式需要事件

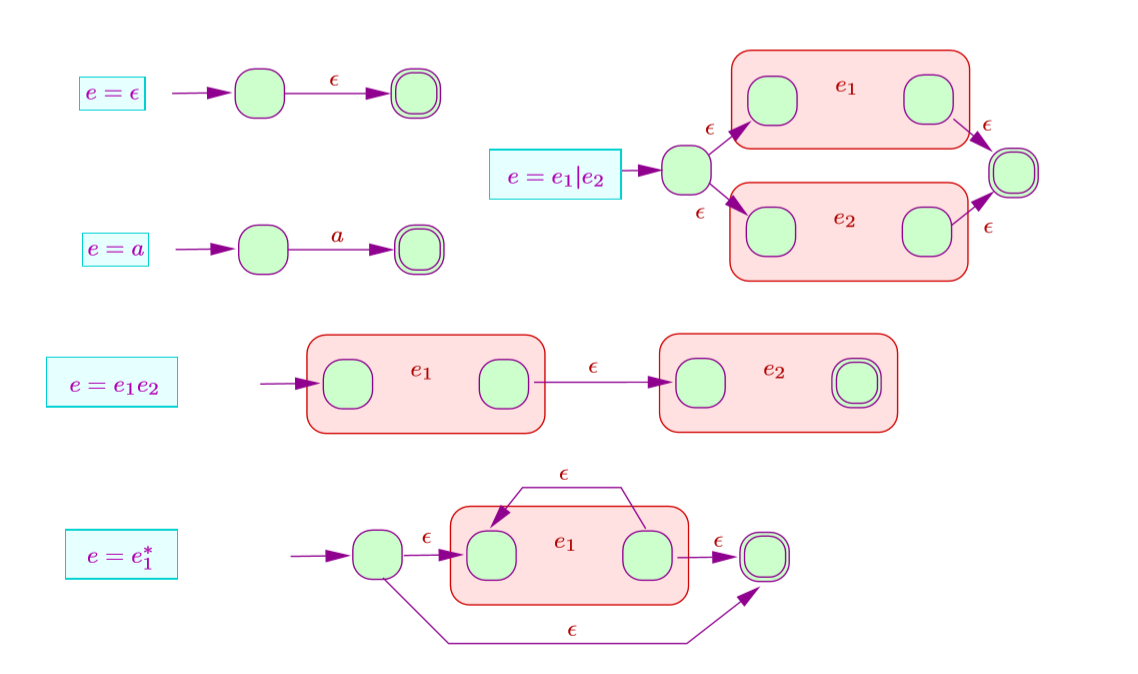
练习1.4：把表达式转换成自动机

Berry-Sethi算法

这个算法可以把一个正则表达式的树，转换成自动机。我们在每个节点的左右都画一个点。左边是入口，右边是出口。

我们使用数字来代替节点

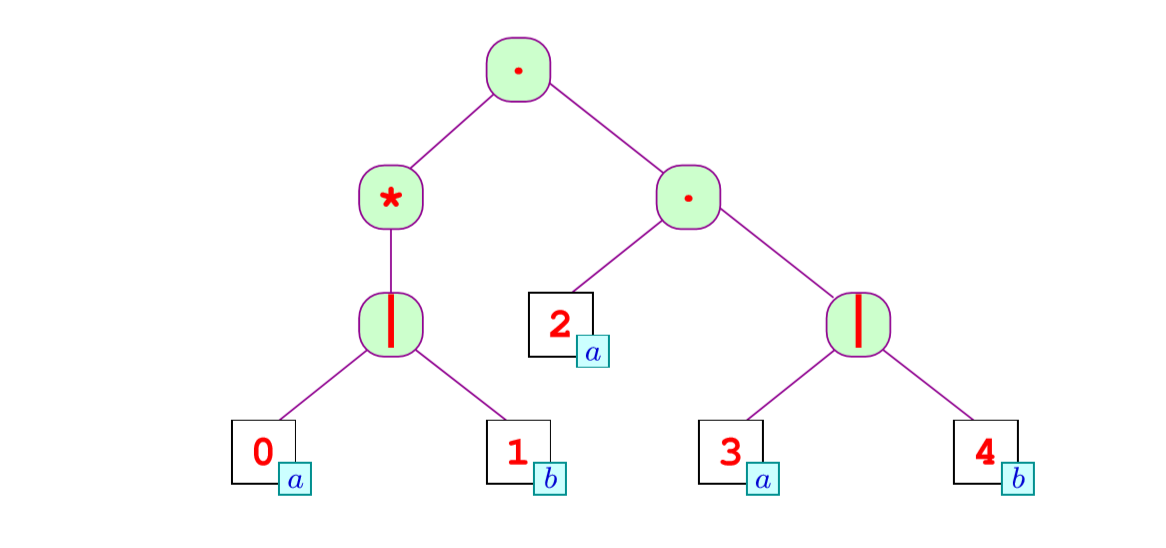
Glushkov Automaton

是使用 Berry-Sethi算法转换完后的自动机

结构如下：

状态:每个节点有左右两个点

开始状态是左边的点，结束状态是右边的点。

转换关系：对于叶子就是左节点到右节点

对于其他的可以用下面的表来表示

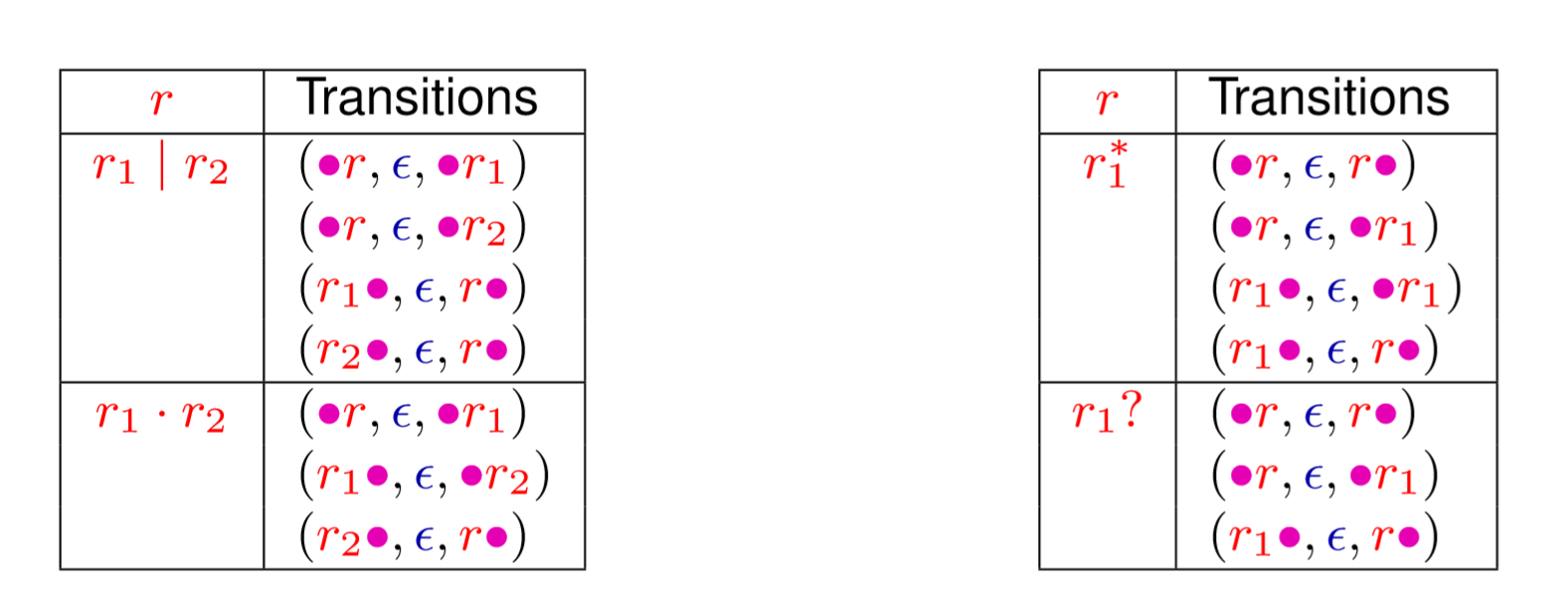
练习 1.5 写出某个正则操作符的转换关系

如果我们直接把这些关系放到语法树上，那么浪费的节点有很多，我们因此要压缩信息

DFS处理标签

我们用DFS处理出下面的标签

ﬁrst 状态点的集合，前面都是
next 这个点的下一个可能的字符
last 这个点最后的字符(到终点是 )
empty 语言中包含的节点

对于empty我们有下面的关系

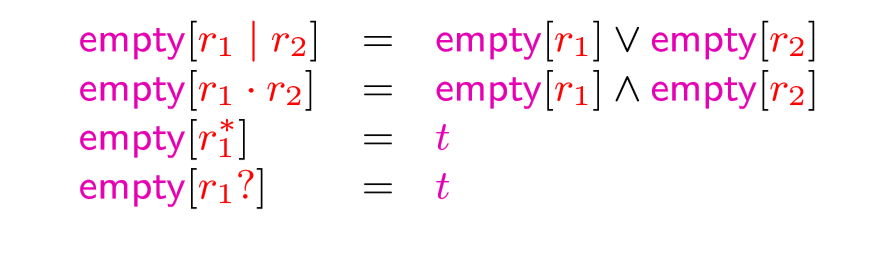
比如对于下面的树就是

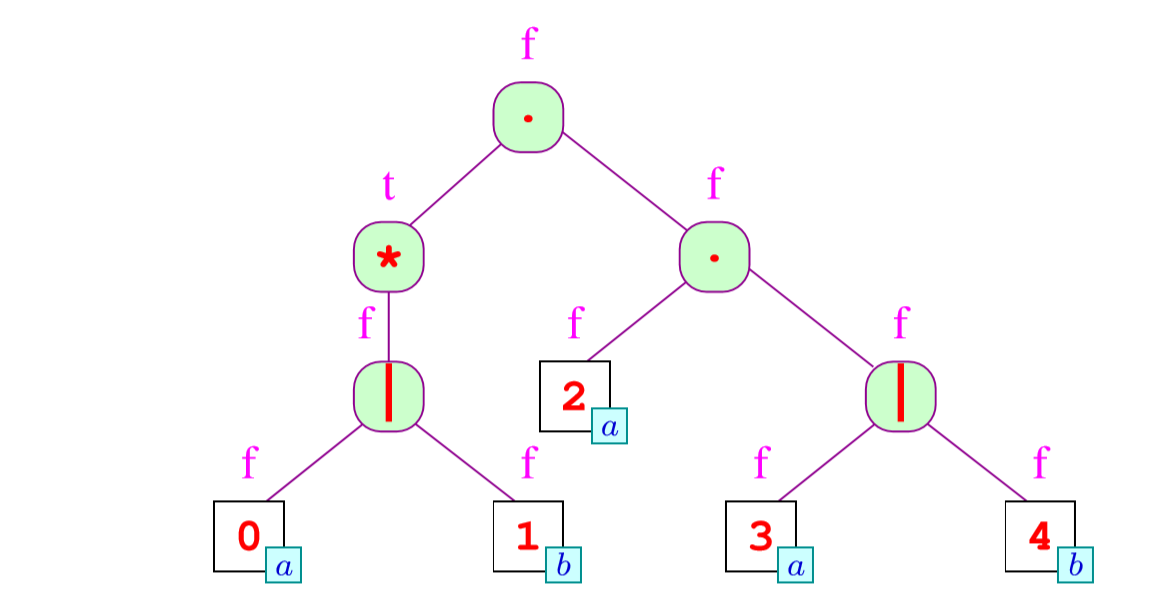
对于first有下面的关系

对应图上就是：

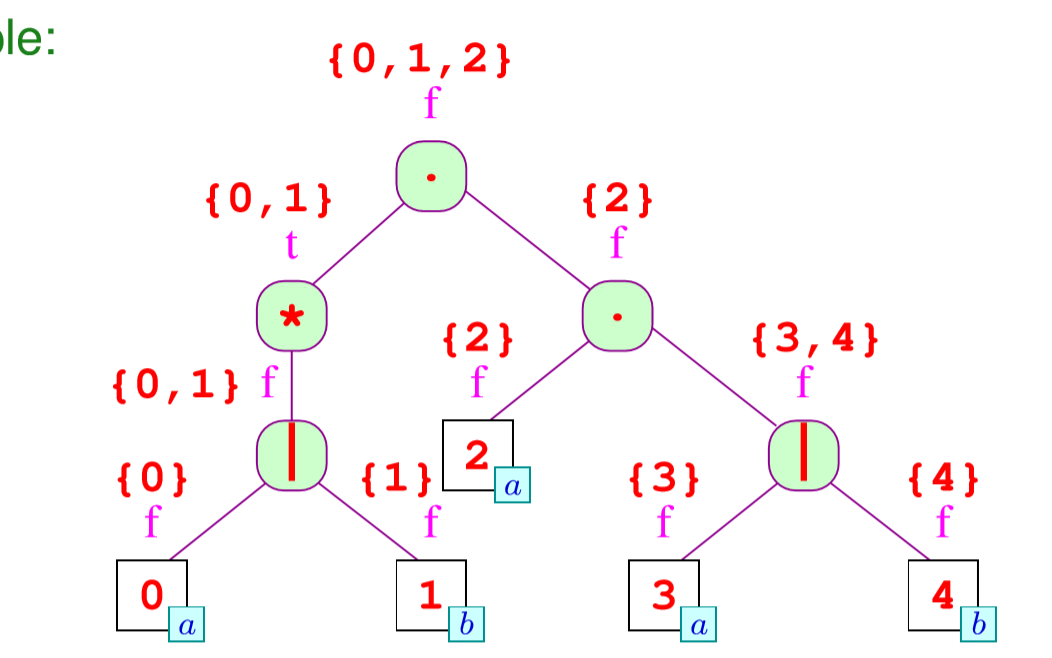
然后我们求next标签，它的关系如下:

我们一般先考虑根节点的出口状态的next是空集，然后一步步倒推来求

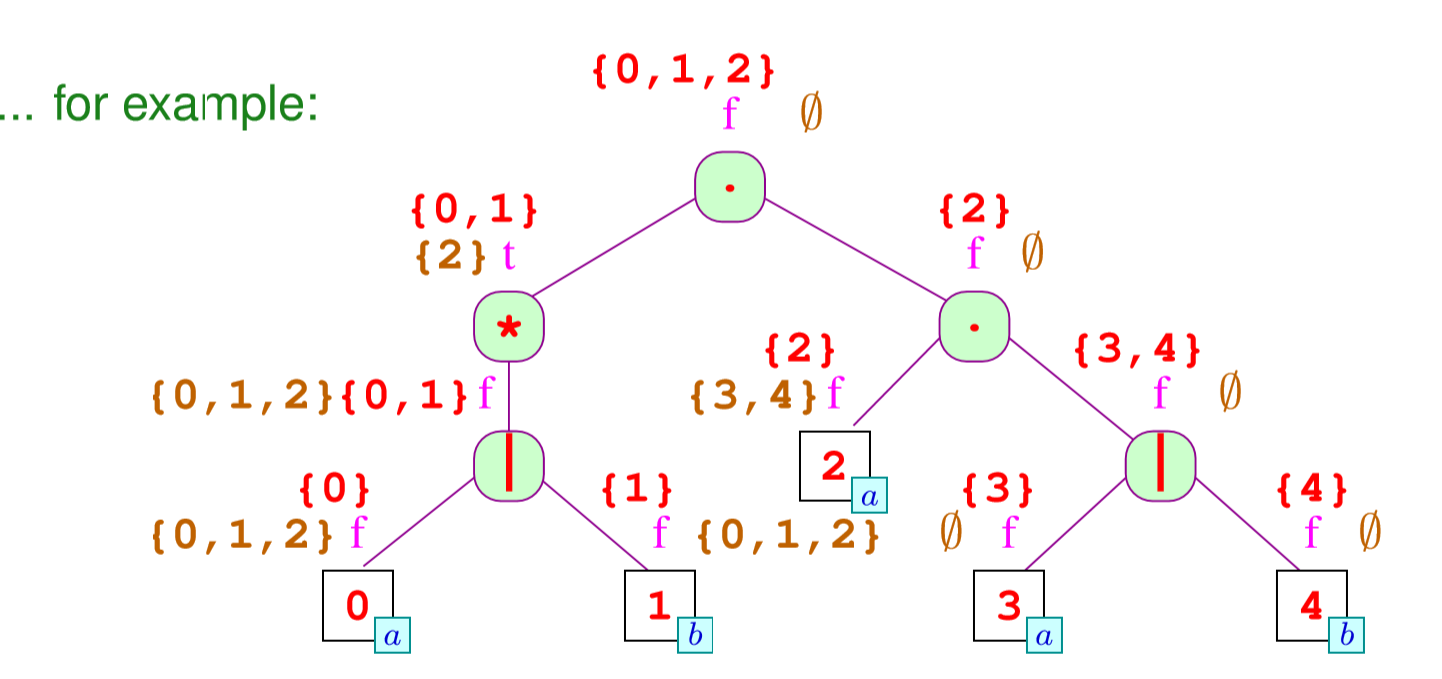
最后我们求last，和求first有点类似

例子上是

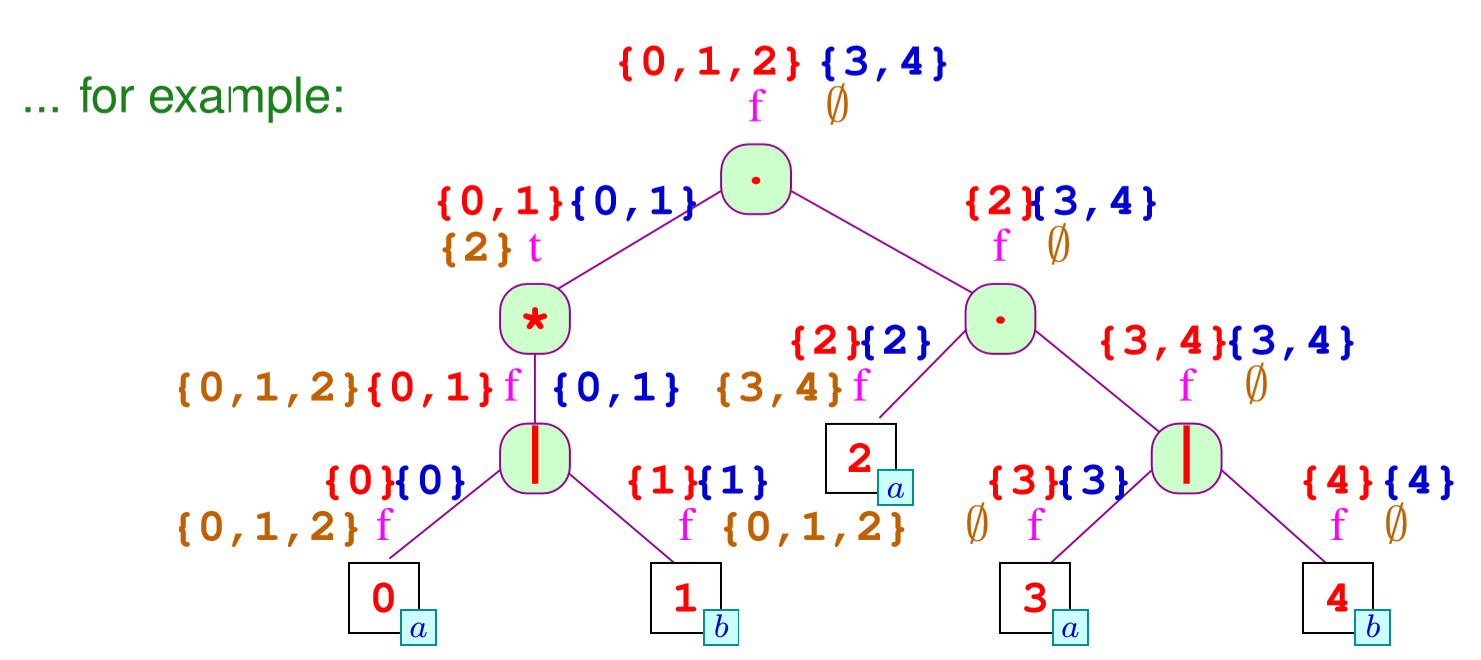
最后我们就有了高级版的Berry-Sethi算法

我们把上述自动机称为 . 比如之前的自动机就长这样：

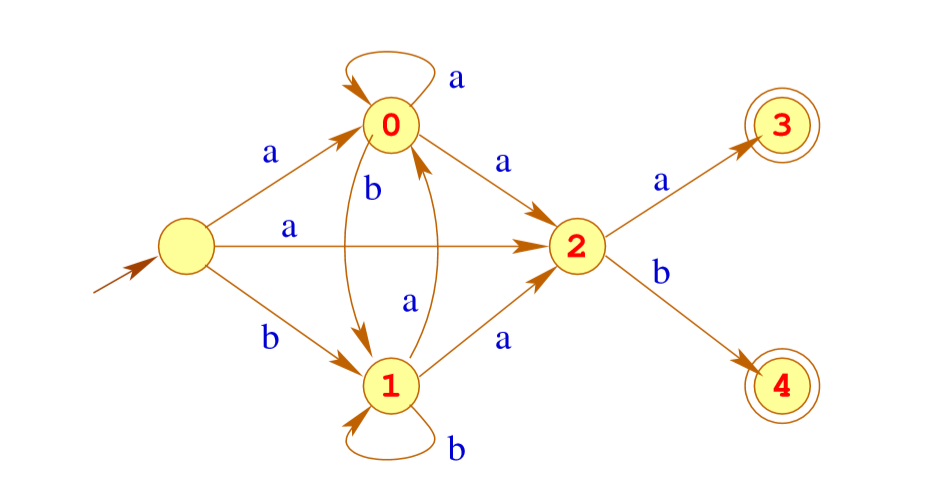
转换NFA为确定的自动机

比如上面的NFA可以使用Powerset来合并一些节点，由此转换

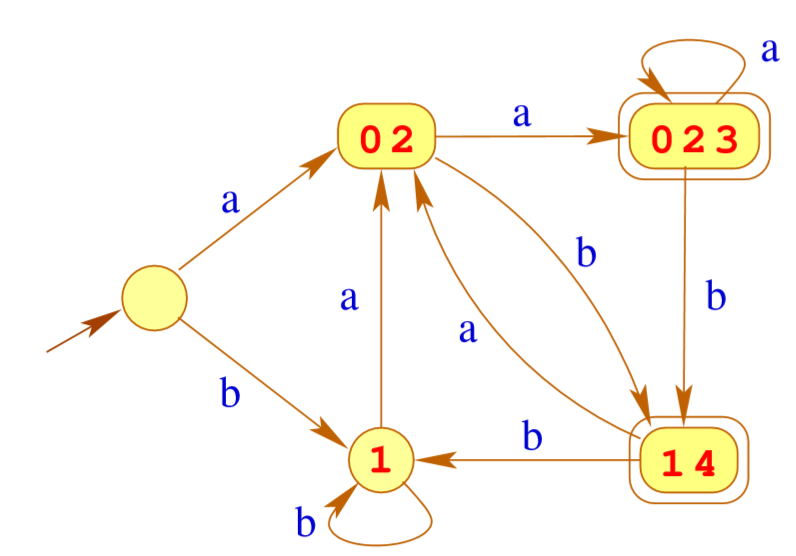
定理

对于每个 NFA: ，我们都可以求一个确定的自动机构造：

状态：的Powersets

开始状态：

结束状态:

转换关系：

但是的Powerset可能有很多很多个，所以我们要根据实际情况来构造Powerset。比如下面这个例子

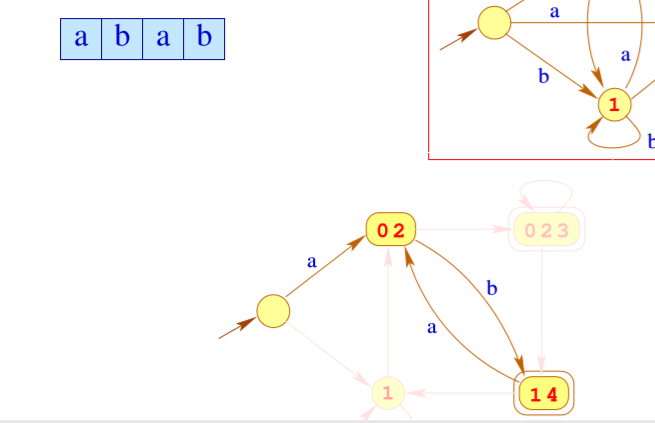
我们只用到了之前的2个Powerset，所以我们就构造2个就可以了。

定理改进

对每个正则表达式我们可以计算出一个确定自动机

设计扫描器Scanner

输入是一组规则，每一个正则表达式对应一个具体动作

输出是一个程序。

它读取最多可以匹配到的字符

然后确定其中一个最小的，使得

然后执行对应的动作

Idea

我们对建立一个NFA ,我们定义下面的集合它们对应了每一个的状态。

对于输入，它匹配到某一个动作，当且仅当

Scanner状态

Scanner可以有不同的状态，我们根据不同的状态来应对不同类型的文本，比如在处理注释的时候。

左边<state> 是Scanner状态，后面是该状态对应的正则表达式和操作是转换到第i个状态。

比如在YYINITIAL中，看到了/* 就要转换到COMMENT状态.在 COMMENT状态下，看到了*/就要转换回YYINITIAL。

语法分析

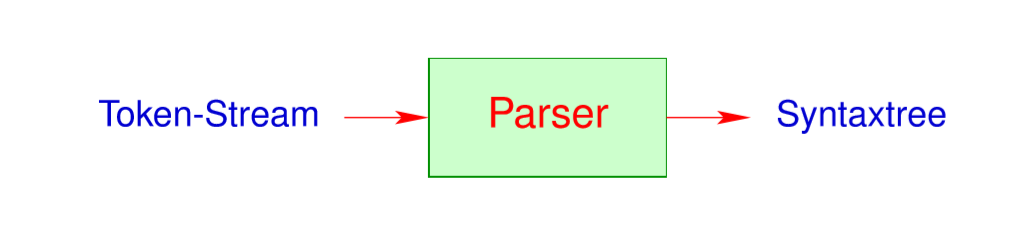
在语法分析 Syntatic analysis的任务是把Tokens变成更大的程序单元，如表达式，条件分支，循环。

Parser并不是用手写，而是生成出来的

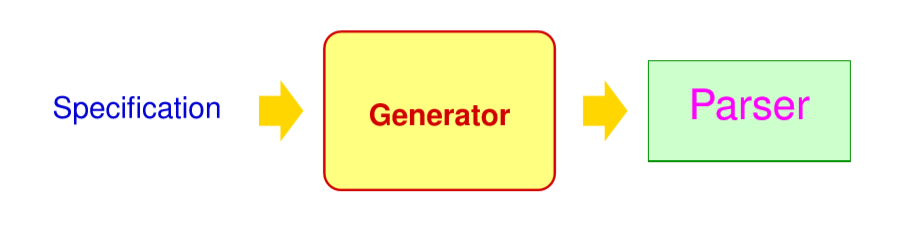
上下文无关文法

一个程序可能有任意多个token，但是只有固定的类别 Token-classes.

定义

一个上下文无关文法(context-free gramar) (CFG)是一个4元组

: nonterminals 的集合就是可以拓展的表达式
: terminals 的集合，无法拓展的表达式
: 规则的集合
: 开始符号

约定 Conventions

Context-free Grammar的格式是这样的：比如

序号

对于每个nonterminal，我们从左到右来记录扩展规则

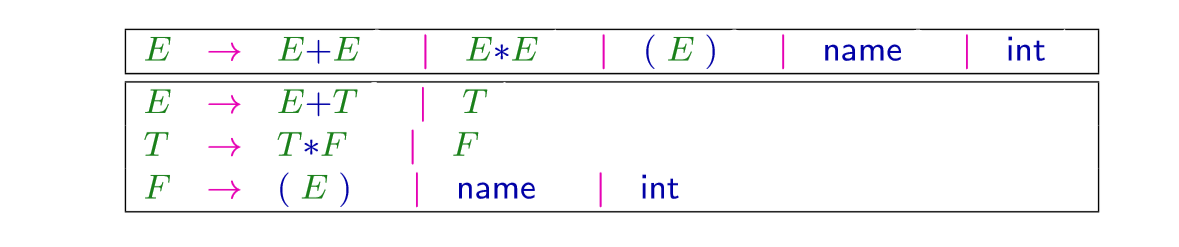
以上这两者描述的是相同的语言

派生 Derivation

一个序列是派生 derivation, 比如

派生树

比如上面的可以这样画

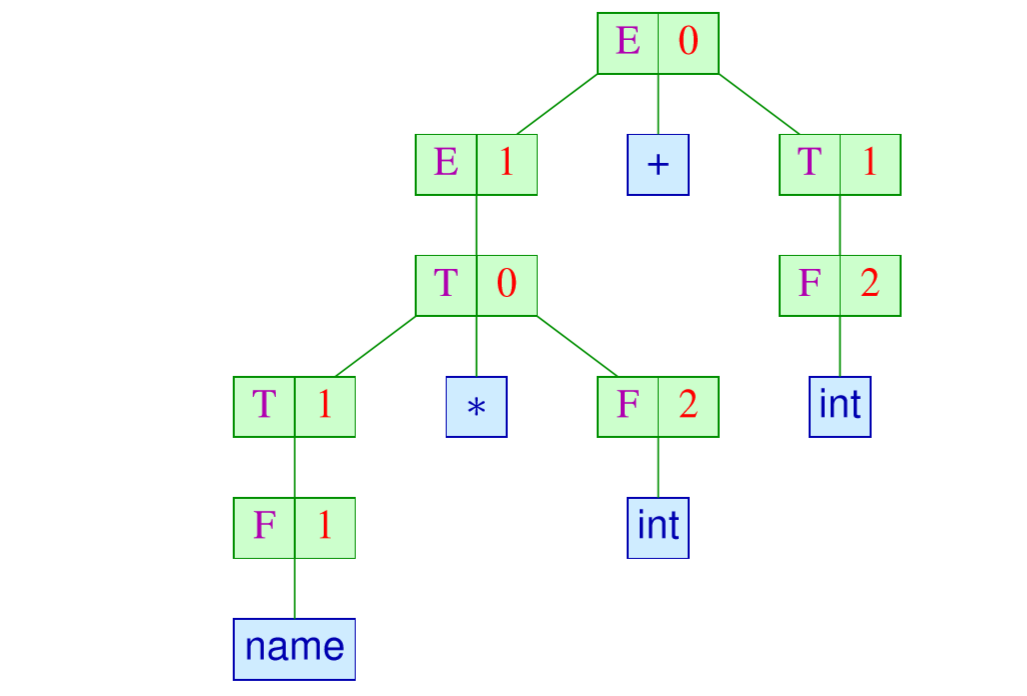
语法的唯一性

一个语法是唯一的，若对于每个只有一个派生树

下推自动机

一个上下文无关文法推出的语言会被下推自动机(Pushdown Automata)所接受

定义

一个下推自动机(PDA) 是一个元组

是状态的有限集
是输入字符集
是开始状态
是中止状态的集合
是传递关系的有限集

比如

从开始状态开始，左边是0，右边第一个字符是a，于是把0替换成右边的11；然后左边第一个字符是1，右边第一个字符是a，所用第二条关系。以此类推…

所以计算关系是 for

确定的下推自动机

一个下推自动机是确定的，若每个设置里有最多一个后继

定理

对于每个上下文无关文法 ,我们可以造一个下推自动机 ,

自顶向下Parsing

Item 下推自动机

它是一个前序遍历构造派生树的下推自动机，比如

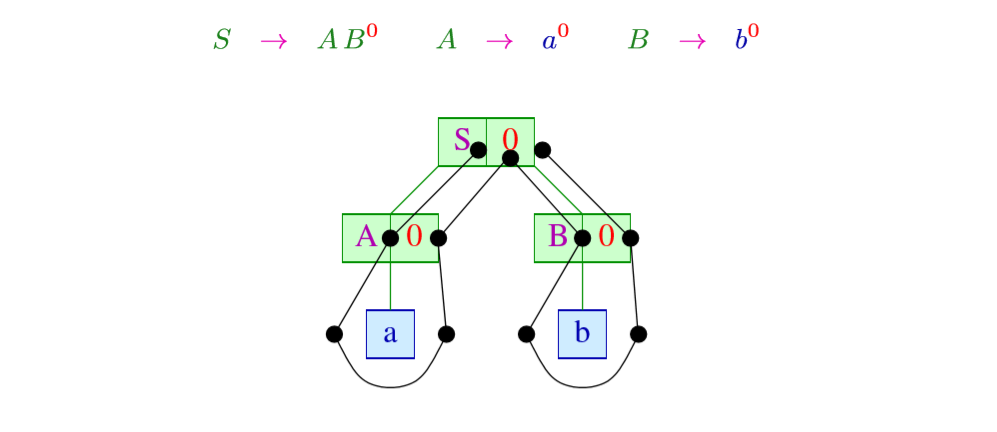
它的转换关系是：

根据上面下推自动机的推导步骤可以推出来这个例子。

我们可以发现他有三种转换关系

Expansions(扩大): ,对于
Shifts(移动点): 对于
Reduces(减少): 对于

问题

有可能会发生歧义，解决办法有2个想法

GLL Parsing

对每个冲突，制造一个虚拟拷贝然后平行计算

回溯

用DFS来回溯

看前面

可以看下一步输入来判断如何解决

LL(1)-Parser 的结构

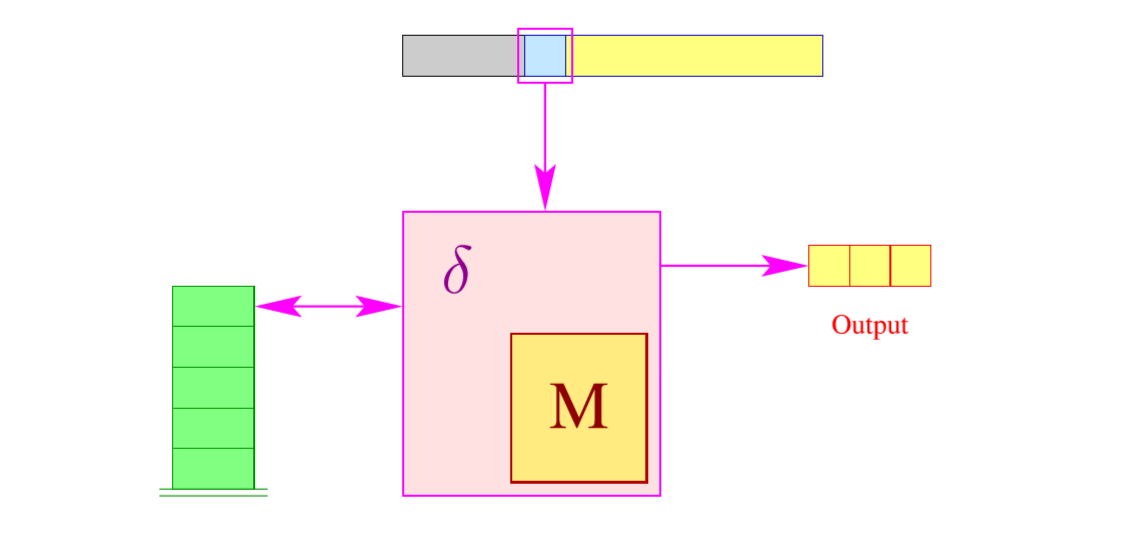
这个Parser访问长度为1的输入。

他对应一个下推自动机

表格包含选择的规则

定义

一个reduced grammer 是若每2个冲突的规则且每次推导 , 下面的是合法的：

向前看集合 Lookahead Sets

定义 - Sets

对于一个集合定义：就是后面可以生成的集合，比如

算数

定义 1-连接

若且 , 那么

快速计算Lookahead Set

Let empty true iff

我们对没有的集合写成一个系统比如

然后我们可以把这些关系写成自动机的形式

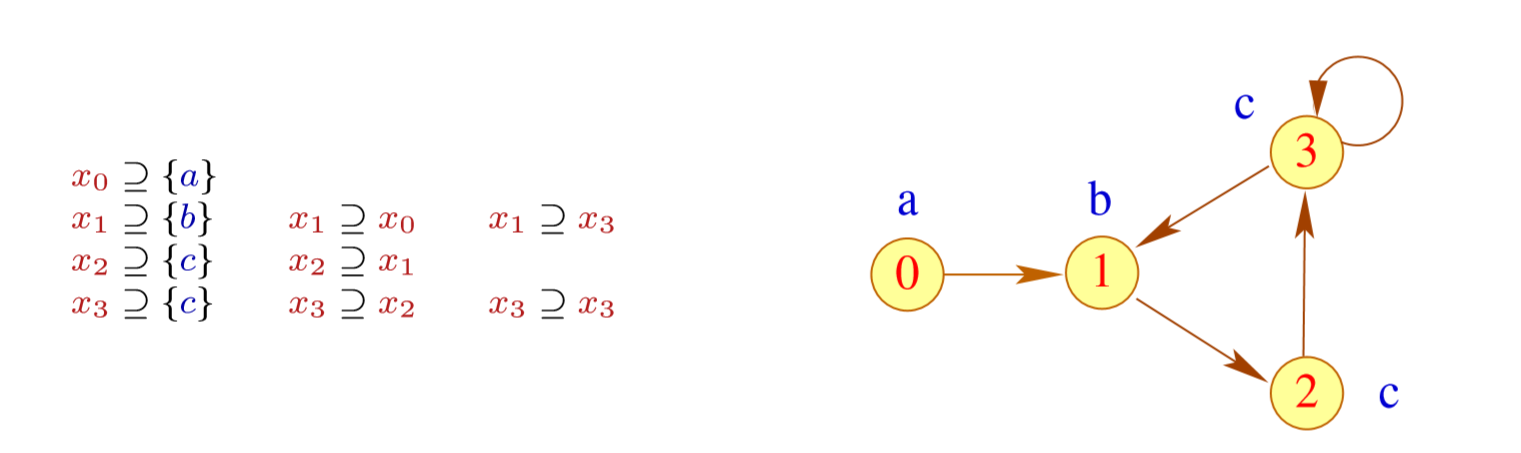
这个是变量依赖图(Variable Dependency Graph) 。然后我们把强连通分量合并。

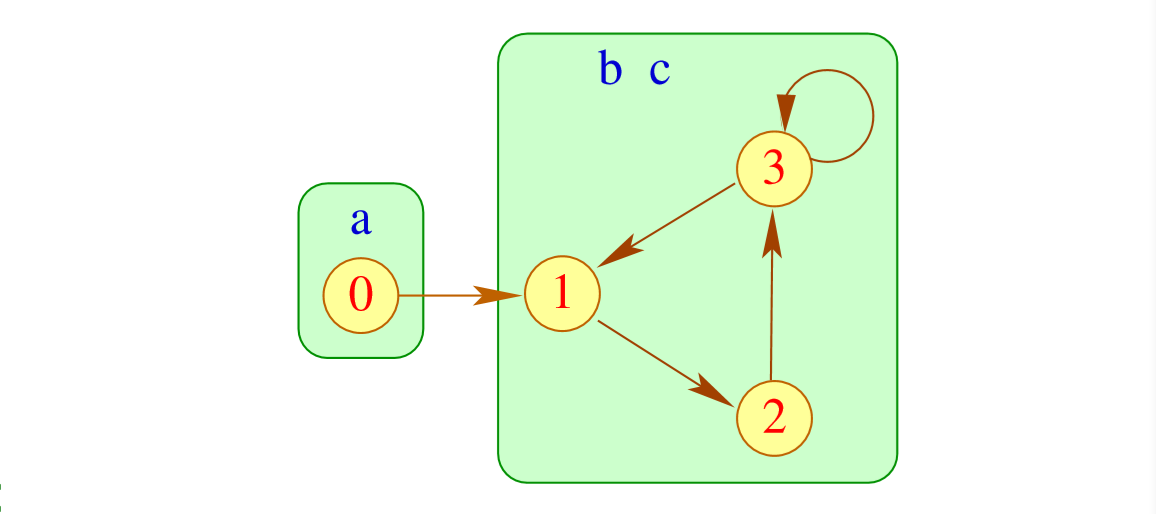
然后我们从没有入度的边开始，把它们的元素加入里面

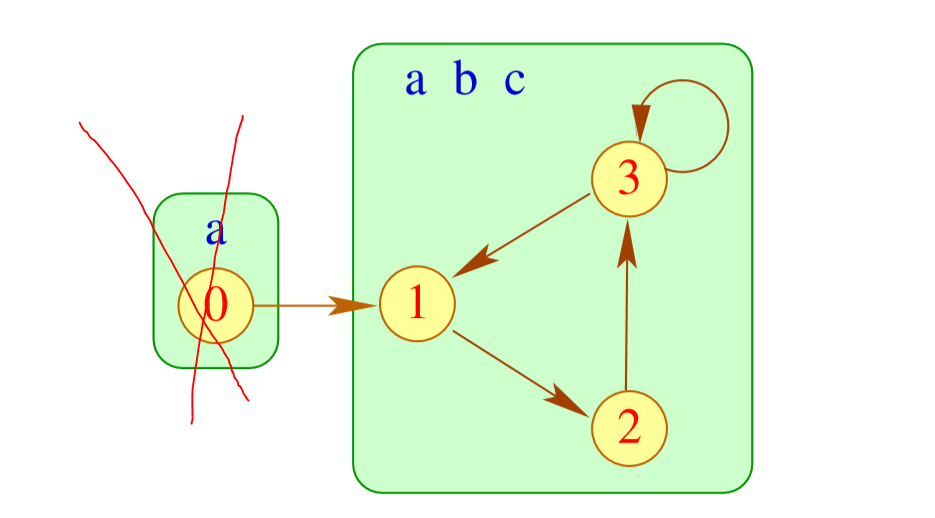
然后就可以把这个点“删掉”.

比如

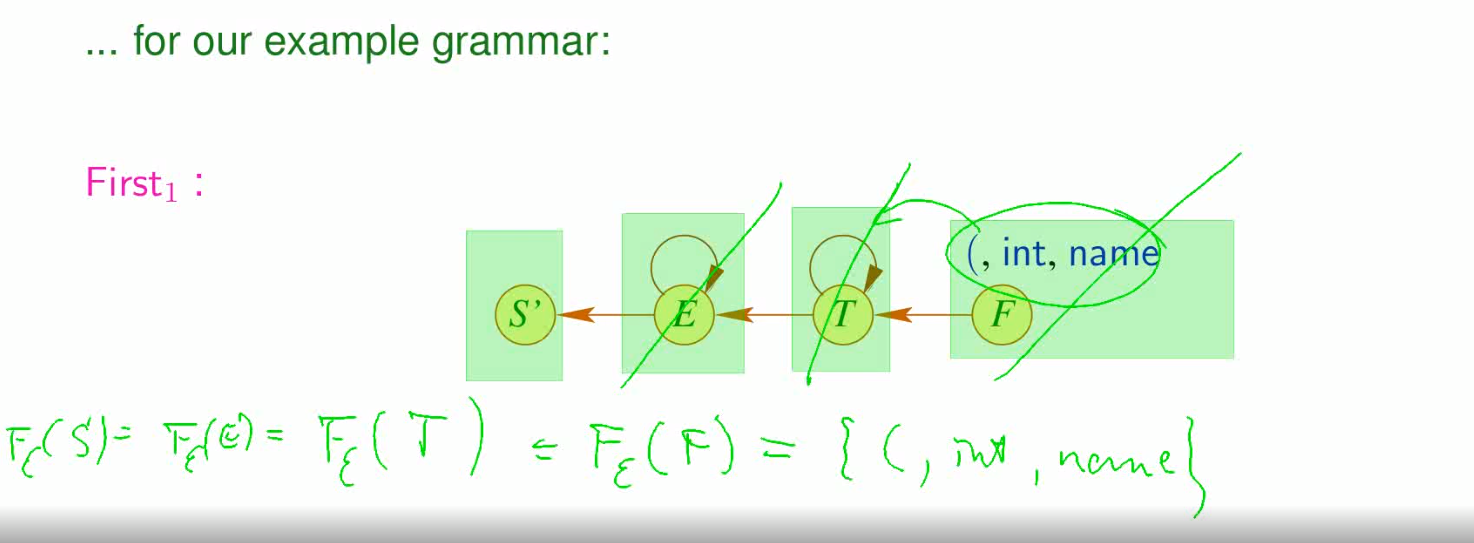
定义 - Sets

也就是的后面是什么

LL(1)-Lookahead Table

我们设表格， if First Follow

比如

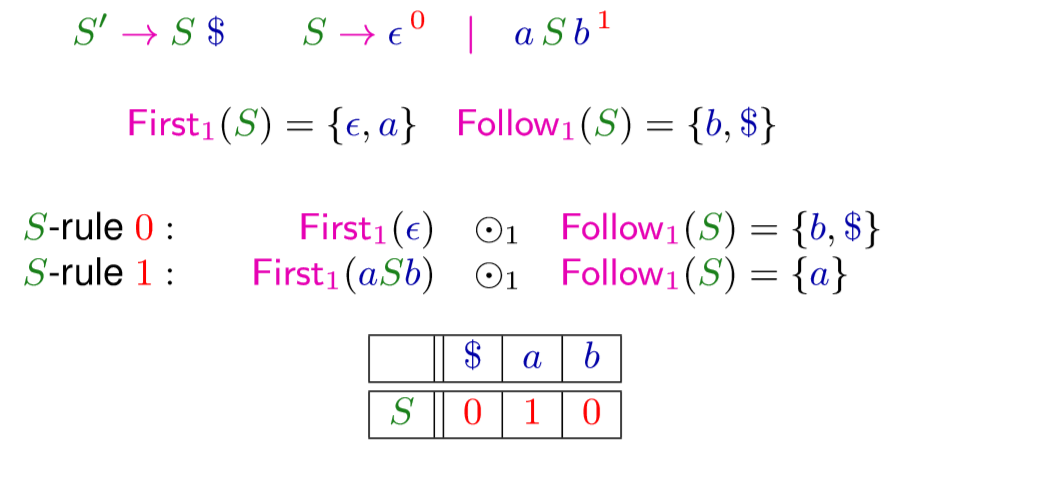
我们就可以根据这个表格来解决冲突

RR-CFG

定义 RR-CFG

一个 right-regular context-free grammar (RR-CFG) 是一个4元组，其中

: nonterminals 的集合就是可以拓展的表达式
: terminals 的集合，无法拓展的表达式
: 正则表达式规则的集合
: 开始符号

例如数学表达式：

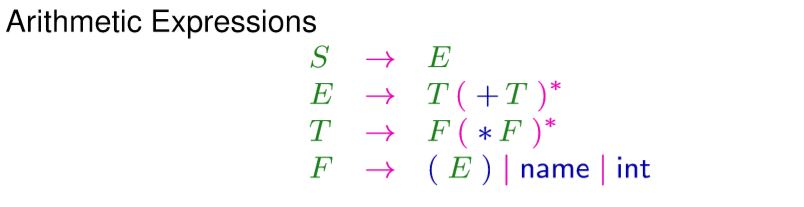
我们可以把这个规则通过添加标签转化一下，拆解开来

转化的规则是

所以上面的可以写成

我们可以得到一个的语法

定义 RLL(1)

一个 RR-CFG 是 RLL(1), 若它的 CFG 是一个语法

Recursive Descent RLL Parsers

Recursive desent RLL(1)-parser 是一个表格驱动的parser

对于 S() 函数是一个生产器

它具体是

对于正则表达式的逻辑可以这样实现