信号与系统

信号系统概念

信号的分类

确定信号：可以用函数描述的

连续信号：在时间内有定义
离散信号

可以写成

随机信号：不能用函数描述的，只能知道概率

周期信号和非周期信号

连续信号的周期

连续周期信号，周期是，满足：比如余弦信号，周期是

若两个周期信号相加，判断是有理数。如果是那就是。

离散信号周期

周期是 :

能量与功率信号

能量等于损失功率的积分，可以想象成是一个1欧姆的电阻的电功率

将信号施加于的电阻上，它所消耗的瞬时功率为 ,于是能量定义为：平均功率：能量有限信号：，此时

功率有限信号：，此时

对于离散信号也有能量信号和功率信号：

因果和反因果信号

因果信号：的信号 ,也就是时接入的信号

反因果信号： (除0信号外)

基本信号

阶跃函数

选的一个函数序列 ,求极限

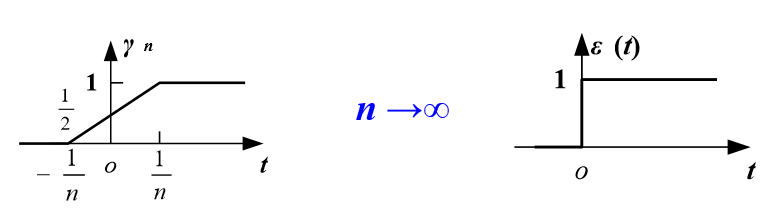
它可以用来叠加表示其他信号，比如

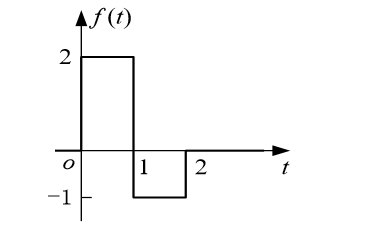
可以表示信号作用的区间

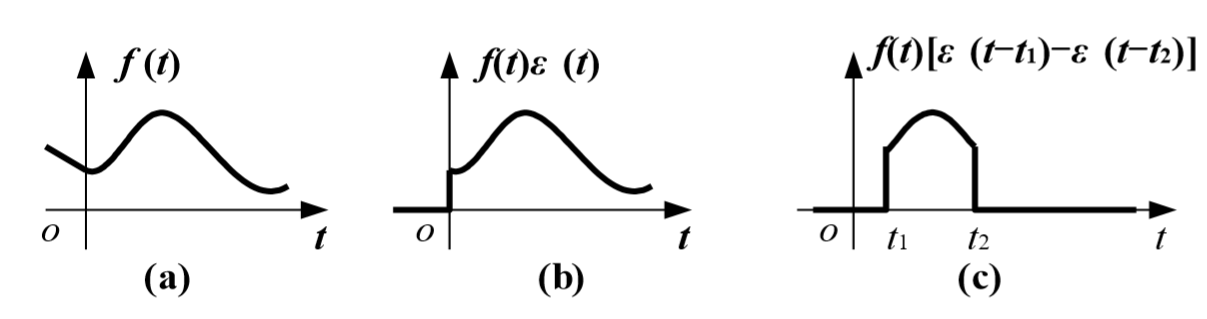
积分

冲激函数

单位冲激函数：是奇异函数，它是对强度极大，作用时间极短的物理量的理想化模型.就是在0这个点冲上去的函数。

理解: 高度无穷大，宽度无穷小，面积为1的对称窄脉冲作用：可以描述间断点的函数

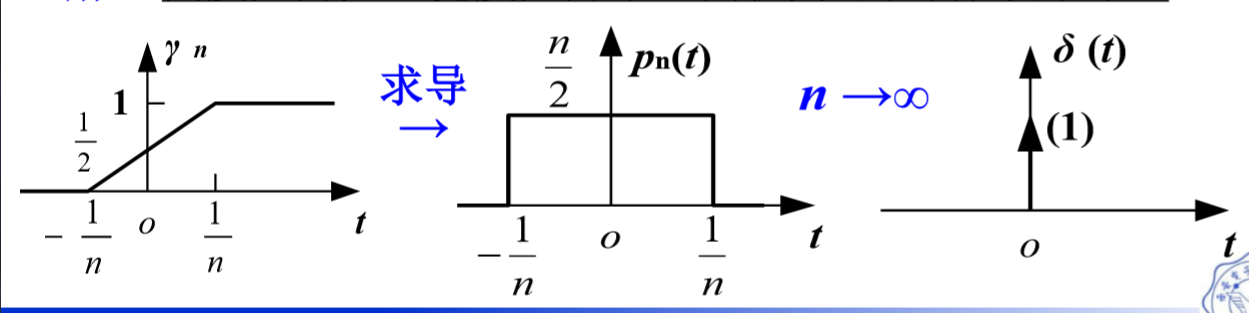
冲激函数的广义定义

广义函数

选择一类性能良好的函数作为检验函数(相当于自变量)，一个广义函数对检验函数空间中的每个函数赋予一个数值N的映射，记为：就是广义函数和检验函数乘一下积分

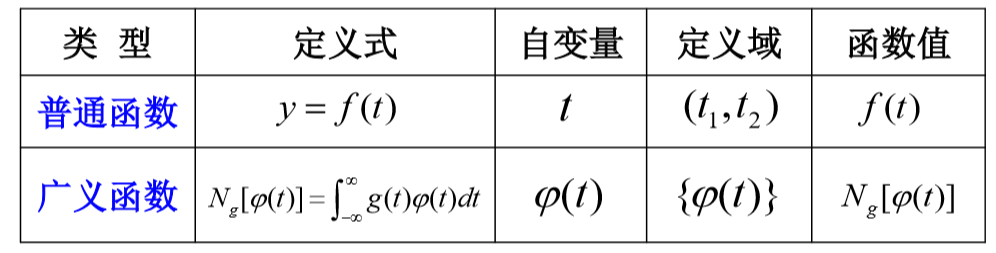
冲激函数的广义函数定义

意思就是能从检验函数中筛选出的广义函数就是冲激函数。比如：

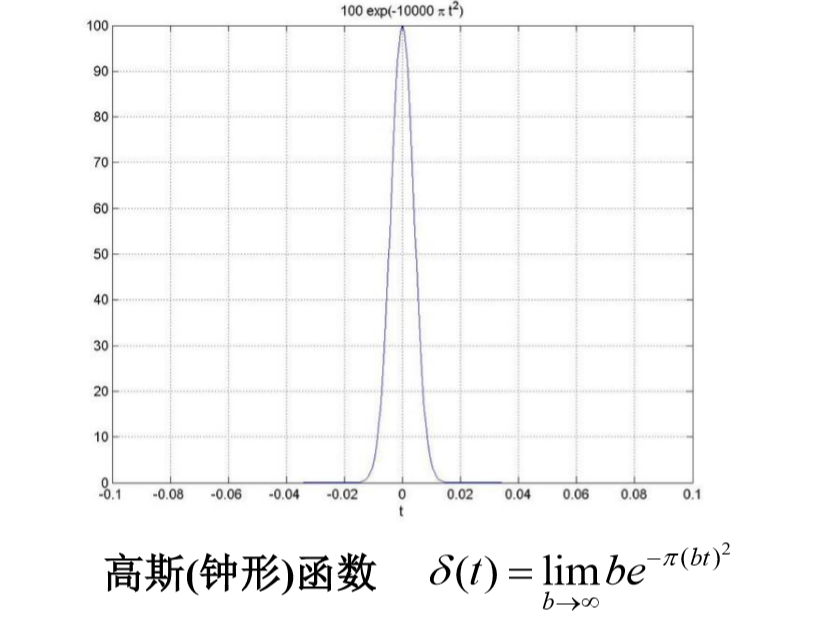
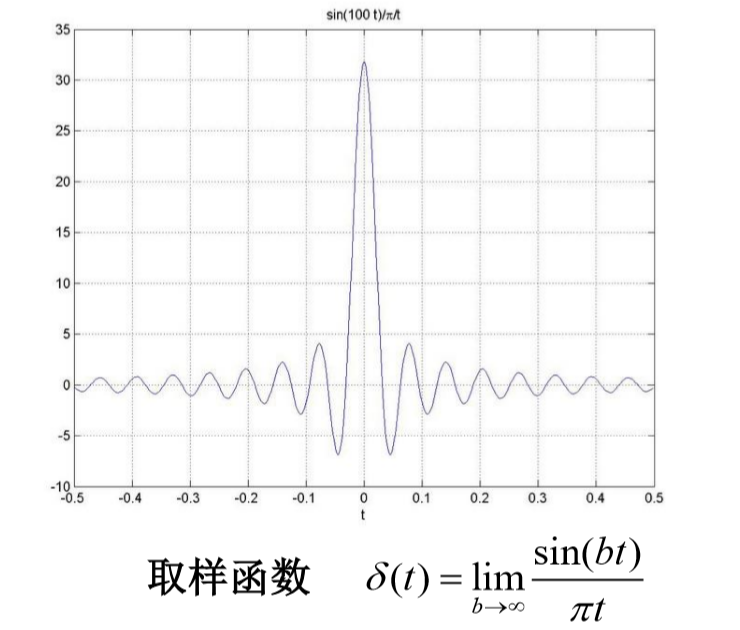
冲激函数的取样性质

积分区间要包含变形一下得到：积分区间要包含

冲激函数的导数

1. （冲激偶）

广义函数定义式：

2. n阶导数

冲激函数的尺度变化

的定义特例：推广结论：当时，$ ^{{(n)}(-t)=(-1)}{n} ^{(n)}(t) $

单位脉冲序列

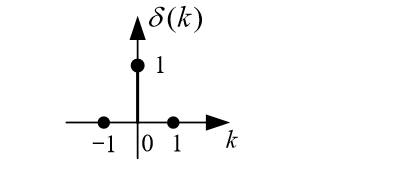
取样性质

单位阶跃序列

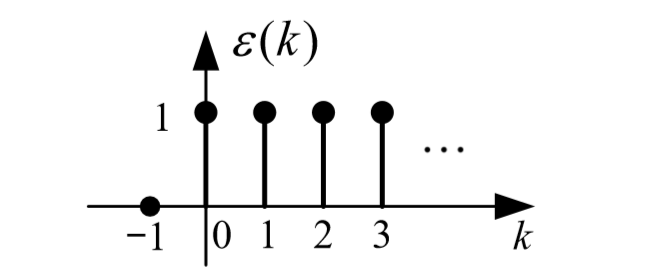
$ ε(k) $与$ δ(k)$的关系

信号的运算

信号的加减乘运算：对于的时刻加减乘

信号的反转

系统

系统是指若干相互关联的事物组合而成具有特定功能的整体。

系统模型

系统模型时对实际系统的理想化。

它分为集中参数模型和分布参数模型。

线性系统

满足线性性质的系统

齐次性：
可加性：
线性性：

这里指的是经过系统的变换

动态线性系统

响应不仅与激励{}有关，而且与它过去的状态{}有关，也称记忆系统。

$输入，状态$ ，是输入，是输出，是状态

完全响应：零状态响应：，由输入产生的响应零输入响应: ，由状态产生的响应

判断条件

若一个动态系统满足三个性质，就是线性系统

可分解性：
零状态线性：
零输入线性：

时变系统和时不变系统

时不变系统：系统输入延时多少少时间，其零状态响应也相应延迟多少时间。不随时间改变。

判断方法：

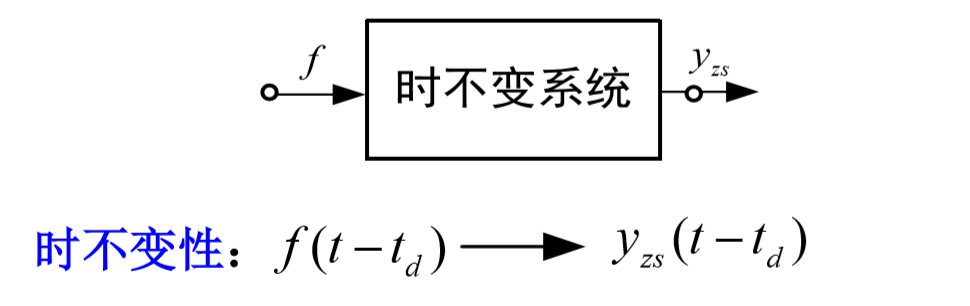
若前由系数，反转，伸缩变换，则是时变系统

我们主要讨论LTI系统(Linear Time-Invariant)，即线性时不变系统

微分特性： $若则$ 积分特性： $若则$

因果系统与非因果系统

因果系统是之零状态响应不会出现在激励之前的系统。

如下列系统均为因果系统：下面是非因果:

连续系统的时域分析

比如RLC电路，可以看作是系统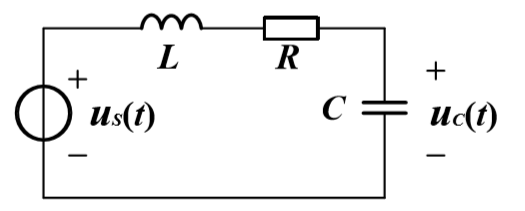

数学模型

可以把物理意义抽去，得到一般的方程可以用相同方程描述的就是相似系统

微分方程模拟框图

我们把上面的方程可以简化写成这个：我们可以通过加法器，数乘器，积分器来表示它

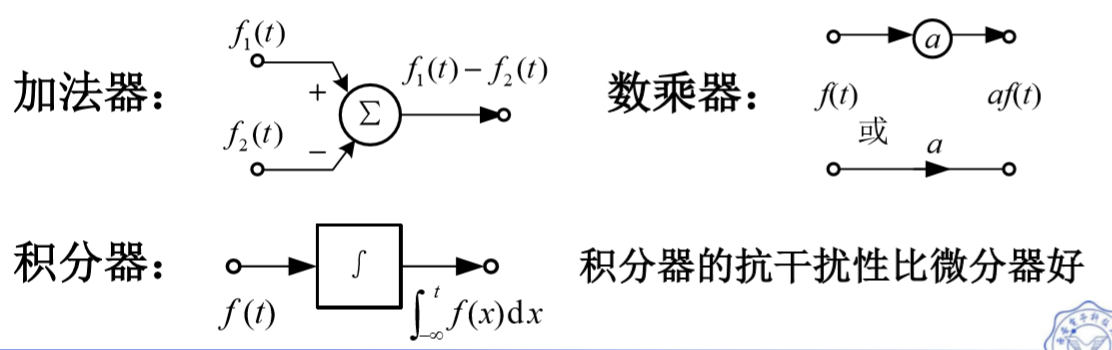
例如上面的方程可以画出：

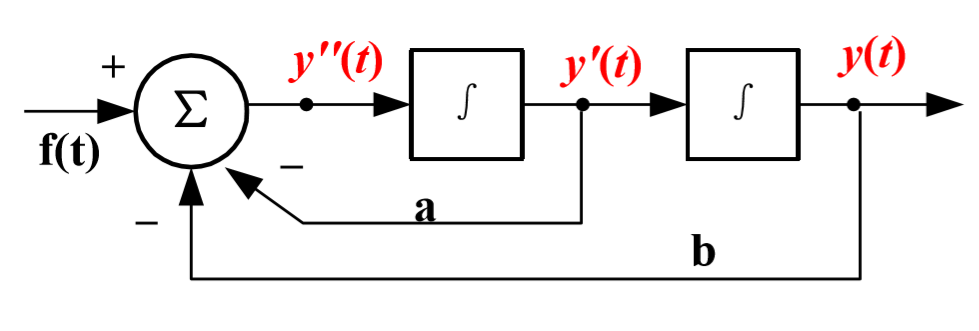
微分方程的经典解法

它的完全解是其次解加特解

其次解是，方程右边等于0的解：可以用特征根得到其次解的函数形式：

特解是原方程中的任意一个解

系统的初始值

初始值是阶系统在时接入激励，其响应在时刻的值，即

初始状态是统在激励尚未接入的时刻的响应值。它反映了系统的历史情况。

零输入/状态响应

零输入

可以分别采用经典发求解

对应齐次微分方程，不存在跃变。

零状态

先求解再用全响应减去它得到零状态响应

响应的分类

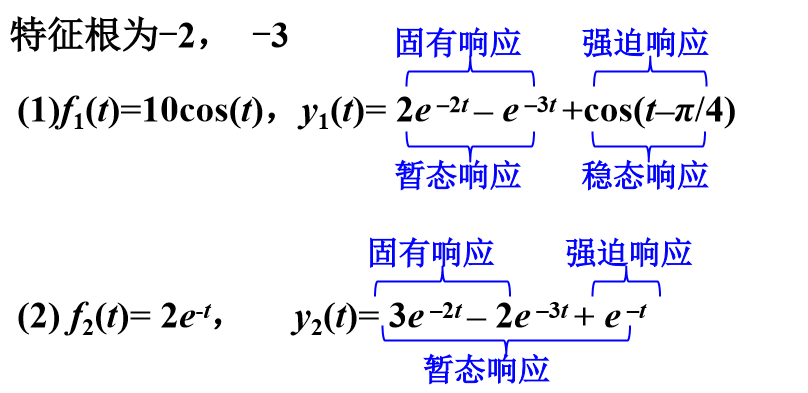
固有响应和强迫响应其次解（和特征根有关）是固有响应，特解是强迫响应
暂态响应和稳态响应暂态响应是t趋近无穷大为0

冲激响应

由单位冲激函数产生的零状态响应, 记为

阶跃响应

由单位阶跃函数产生的零状态响应, 记为

卷积公式

信号时域的分解

对于任意信号，我们构造一个相近的信号来逼近它

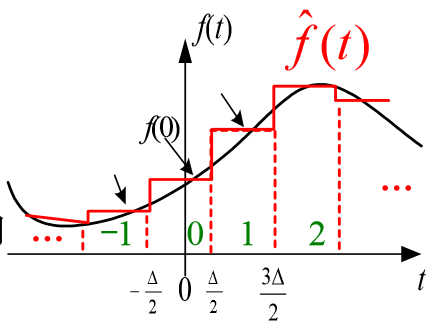
卷积公式

卷积积分 已知定义在区间上的两个函数和，则定义积分为函数和的卷积积分，简称卷积，记为

卷积性质

卷积满足乘法的交换律，分配律，结合律。

复合系统的冲激响应

并联是相加，级联是卷积运算

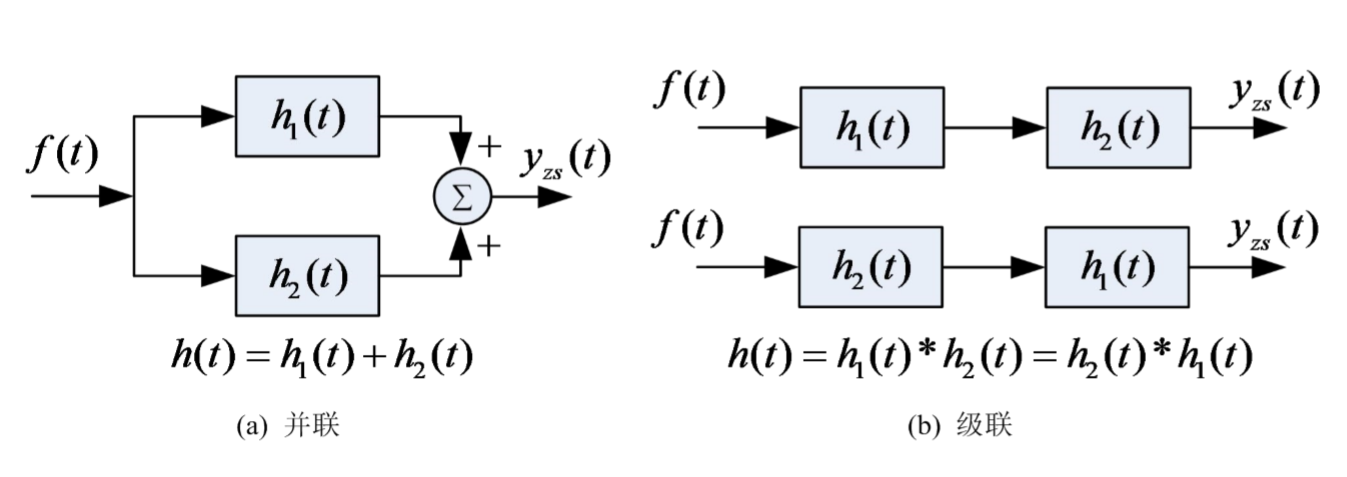
奇异函数的卷积特性

卷积的微积分性质

卷积的导数，是其中一个的导数再卷积卷积的积分，是其中一个积分然后再卷积下面一个最重要, 一个函数求导，一个函数积分：

在或前提下，