概率论

离散概率空间

基础部分

定义1 离散概率空间

离散概率空间(diskreter Wahrscheinlichkeitsraum)是单位元事件(Elementarereignis)的所有结果集合(Ergebnismenge) 。

定义2 单位元事件

每个事件元素 都对应一个可能性 ,其中, 并且 #### 定义3 事件

集合 是事件，该事件的概率是 事件 是事件 的对立事件(komplementäres Ereignis)。两个事件是分离的(disjunkt/unvereinbar)若 .

定义4 相对频繁度(relative Häufigkeit)

定义5 无限概率空间

概率空间 是有限概率空间。关于无限概率空间，我们只考虑 ，也就是离散的情况

例子

假设我们扔一个硬币，直到正面出现。 是反面出现的概率，正面出现的概率是 .那么概率空间我们可以表示为丢硬币的次数直到正面出现。 设 仍硬币 次的事件元素。那么 . 并且： #### 数学公式补充

定理8 性质

对于事件 有：

• 若 ，那么

• 加法原理：若事件 两两互斥，那么有

定理9 容斥原理(Siebformel)

容斥原理：对于事件 有 容斥原理 推论 Prinzip von Laplace:

条件概率

对于条件概率 有如下的性质

• 对于给定的 ， 正比于

定义12 条件概率

和 是事件且 . 那么条件概率 是如下定义的： 在事件 基础下的概率空间：

定理16 乘法原理

若事件 ，且 ,那么

定理18 全概率公式

若事件 ，两两互斥，且 那么 如果事件有无穷多个，那么：

定理19 贝叶斯公式

事件 两两分离，且 对于所有事件。 ，且 ，那么 若事件有无穷多个，那么

独立性(独立性)

若 也就是 若 那么，这两个事件是独立的(unabhängig)

对于两两不同的事件 独立，若对于所有的子集

， 有

定理 23

对于两两不同的事件 独立，若对于所有

有 其中 且

定理24

若 是独立事件，那么 与 且 与 也独立

随机变量

定义25 随机变量

给定一个离散概率空间 一个映射 是随机变量 (Zufallsvariable)

值域(Wertebereich)是

扔硬币3次，结果集合是 也就是正反的三元组。随机变量描述了出现正面的总数。 比如 出现正面2次, 出现正面3次,值域

是逆映射，通常我们把 写作

定义27 概率密度函数和分布函数

• 函数

称作随机变量 的概率密度函数(Dichte)

• 函数

称作随机变量 的分布函数

求密度函数：从值域入手，把每个值都对应写出来。

求分布函数：先求密度函数，然后把密度函数累加

定义 29 期望

对于一个随机变量 ,我们定义期望值(Erwartungswert) 为： 若 收敛

计算期望

判断期望是否存在，要加绝对值算。

定理 32 期望的单调性

若 是在离散概率空间 的随机变量，且满足 对于所有， 那么

定理 33 期望的线性性

对于任意随机变量 , 有

定理 34 期望计算公式

若 是随机变量且 ,有

定义 35 条件期望

若 是随机变量，且 是事件，且 那么条件随机变量(bedingte Zufallsvariable)的密度是 期望值是

定理 36 条件期望计算期望

若 是随机变量，对于两两独立事件 , 且 ，有

定义 38 方差和标准差

对于随机变量 且 ，我们定义(Varianz)方差 为 大小(Größe) 是 的标准差

定理 39 方差和期望

对于任意随机变量 有：

定理 41 方差公式

对于任意随机变量 和 有

定义 42 矩

对于一个随机变量 我们说 是k-te Moment(k阶4矩) 且

是 k-te zentrale Moment(k阶中心矩)

多变量

函数 是随机变量 的总密度(gemeinsame Dichte) ，其中 函数 和 是Randdichten

把其他变量的所有情况带入式子求和即可

随机变量的独立性

定义45 独立性

对随机变量 是相互独立的(unabhängig)，若对于所有 满足： 或者

定理46 独立性扩展1

若 是相互独立随机变量，且 是任意的集合 ，那么 ,,“, …,,“ 都是独立的

定理47 独立性扩展2

若 是实数函数 . 当随机变量 相互独立，那么对于所有 也相互独立。

组合随机变量

定理49 独立的随机变量加和

对于2个相互独立的随机变量 若 ，那么满足

组合随机变量的矩

定理50 期望的线性性

对于随机变量 和 , 满足

Beispiel 51:

个人随机到 个床位，期望有多少个人在自己的床位上？

先拆解：

因为

所以

定理52 期望的乘积性

对于相互独立的随机变量 ，满足

定义53 指示函数

对于一个事件 ，随机变量 是事件 的指示变量 Indikatorvariable

定理54 方差加和

对于相互独立的随机变量 且 满足：

重要分布

伯努利分布

一个随机变量 ， 并且密度是 是伯努利分布(Bernoulli-Verteilung)。参数 是成功概率(Erfolgswahrscheinlichkeit).

比如扔硬币是只有正或反，满足伯努利分布

二项分布

定义 55 二项分布

若 是 个独立的伯努利分布随机变量的加和，并且他们有相同的成功概率 . 那么 就是二项分布，参数是 和 . 符号是

,

比如连续扔硬币n次，满足二项分布

定理 56 二项分布加和

若 和 独立，那么满足 , 且 .

几何分布

定义57 几何分布

一个几何分布的(geometrisch verteilte) 随机变量 ，参数 且 有密度函数 对于它的期望和方差：

一个性质

成功概率和已经尝试的此数无关：

比如一直扔硬币，知道正面出现。满足几何分布

求大于某个值的概率

泊松分布

泊松分布(Poisson-Verteilung) 可以用于建模在给定时间段有固定变化率且独立的固定事件的个数。

一个泊松分布变量 ，参数 有值域 并且有密度函数： 写作

而且方差和期望满足

定理59 泊松分布随机变量加和

若 和 是独立的随机变量满足 和 ， 那么满足

求解泊松分布常用到 的幂级数展开式

泊松分布与二项分布

当 时，且 相对于 足够大，二项分布与泊松分布近似

概率的估计

不等式

定理60 马尔可夫不等式

若 是随机变量，它只有非负值。那么对于所有 且 满足 或者：

用于估计概率的上界 (Blatt6 H01)

定理 61 切比雪夫不等式

若 是随机变量, 且 ,满足 或者：

用的时候可以用绝对值的性质拆开绝对值(Blatt6 H01),

大数定律

定理 63 大数定律

给定一个随机变量， 若 是任意且固定的。那么对于所有 ：

若 独立随机变量且拥有和 相同的分布,且设 那么满足

切诺夫界

定理 64 切诺夫界 1

若 是独立的伯努利分布的随机变量，且， . 那么对于 und ， 满足

定理 66 切诺夫界 2

若 是独立的伯努利分布的随机变量，且， . 那么对于 und ， 满足：

引理 67 切诺夫界扩展

对于 满足

推论 68 推论公式

若 是独立的伯努利分布的随机变量，且， . 那么对于 und

• für alle
• für alle
• für

概率生成函数

定义70 概率生成函数

对于一个随机变量 , 那么概率生产函数 (wahrscheinlichkeits-)erzeugende Funktion为

定理71 函数的唯一性

一个随机变量 , 的密度和分布是通过它的生产函数唯一确定的.

伯努利分布

均匀分布

若 在 均匀分布，也就是对于 ，

二项分布

几何分布

泊松分布

计算期望方差

定义74 秩生成函数

对于一个随机变量 ，秩生成函数 momenterzeugende Funktion 是

随机变量加和

定理75 和的生成函数

对于独立随机变量 且 ，那么满足 而且

随机和

我们考虑这样的情况： ， 是一个随机变量.

定理77 和的生成函数

若 是独立，而且具有相同分布随机变量，生成函数是 . 是一个独立随机变量且有生成函数 . 那么随机变量 有随机生成函数 .

连续概率空间

连续随机变量

定义79 连续随机变量

一个连续的随机变量 (kontinuierliche oder auch stetige Zufallsvariable )和它在的连续概率空间(kontinuierlicher (reeller) Wahrscheinlichkeitsraum)是由一个积分函数定义的 : 可以通过对可数且分离的区间并集 构造出的集合 叫事件(Ereignis). 的概率是这样算的：

根据性质计算参数 (Blatt7 T02)

Kolmogorov-Axiome和σ-代数

定义82 σ-代数

若 是个集合。 是在集合 上的 -代数(Algebra), 若下面的性质满足：

• 若 那么
• 对于 设 那么

对于所有 是一种 Borel集合.

判断集合是否是 σ-代数 (Blatt7 T01)

定义83 柯尔莫哥洛夫公理Kolmogorov-Axiome

若 是个集合。 是是在集合 上的 -代数. 映射 是 上的概率测度(Wahrscheinlichkeitsmaß) ，若满足：

• 是两两互斥的事件. 那么满足：

对于一个事件 , 是 的概率(Wahrscheinlichkeit). 一个概率空间是由元组 定义的.

引理84

若 是一个概率空间。对于事件 满足：

• 若 则

• (加法原理) 当事件 两两互斥，那么

勒贝格积分

一个函数 是可测量的(messbar). 若每个Borel波莱尔集合的原像(Urbild)还是一个Borel集合，

每个可测量的函数都可以积分，叫做勒贝格积分(Lebesgue-Integral).

• 连续函数都是Borel波莱尔可测的(Borel-messbar)
• 指示函数 是Borel可测的
• Borel可测的函数与Borel可测函数的和和积也是Borel可测的

判断一个函数是否是Borel可测 (Blatt7 T02)

计算连续随机变量

连续随机变量函数

若 ， . 那么 的分布是 这里 是所有实数满足 “” 的.

求密度函数：先求分布再求导

求一个函数是否是分布函数：

1. 非严格单调增
2. 连续
3. 在负无穷的极限是0，正无穷的极限是1

连续随机变量极限

若 是一个连续随机变量，我们可以从 里构造一个离散的随机变量。设 ，那么 对于 满足

期望和方差

定义88 期望和方差

对于一个连续随机变量 ，方差如下定义： 只要 是有限的.

对于方差是 当 存在.

引理89 计算期望

若 是连续随机变量, 令 那么

使用公式计算期望和方差 (Blatt07 T02)

重要连续分布

均匀分布

正态分布

定义 91 正态分布

记为

分布函数 若 也叫标准正态分布，标准正态分布的分布函数也叫高斯-函数。(一般可以查表看值)

高斯函数的性质

对于 满足

引理 92 定义

定理 93 正态分布的线性变换

若 是一个正态分布的随机变量. 那么对于任意的 和 . 也是正态分布

定理 94 N(0,1) 期望方差

若 是 分布，那么

定理 95 N 期望方差

满足 分布, 那么

秩生成函数

若 是正态分布

指数分布

定义 96

一个随机变量 是以 的指数分布. 若满足密度函数 分布函数为

,

定理 97 指数随机变量的缩放

一个随机变量 是以 的指数分布. 对于 的随机变量 也是一个指数分布的随机变量, 参数 .

定理 98 无思想性

一个连续随机变量 是指数的，当且仅当对于所有 满足

指数分布与几何分布的极限

设一个几何分布的序列 , 参数为 . 当 时， 可以用 , 是参数为 的指数分布来逼近。

多个连续随机变量

多元密度函数

两个连续随机变量 可以这样表示 ： 对于事件 :

定义 100 边缘分布Randverteilung

若 是随机变量 的密度函数. 那么 边缘分布Randverteilung 是 类似的 是 的边缘密度函数Randdichte

定义 101 独立性

两个连续随机变量 是独立的，若对于所有 满足 类似的也有

多个事件的等待问题

定理 102 指数分布最小值

随机变量 是独立的且是以参数 指数分布. 那么 也是指数分布，以参数 .

泊松过程

对于给定 , 是独立的相同的指数分布的随机变量,每个参数为 是泊松分布的随机变量，参数为

定理 105 随机变量加和

若 是独立的连续随机变量，对于 满足

定理 106 正太分布的加和

随机变量 是独立的且是以参数 正态分布. 那么 也是正态分布，期望值为 方差为

连续变量秩生成函数

连续随机变量和离散随机变量有相同的秩生成函数

中心极限定理

定理108 中心极限值定理

随机变量 有相同的分布且都互独立. 且期望和方差都存在并且记为 和 .

随机变量 定义为 . 那么 是渐进的标准正太分布，也即是 对于

定理 109 de Moivre 棣莫弗—拉普拉斯定理

随机变量 是伯努利分布且都互独立，有相同的成功概率 .那么

对于 , 分布函数为

当 时, 是渐进标准正态分布

定理 110 正太分布对于二项分布的极值

若 $H_{n} (n, p) H_{n} / n$ 趋近于 对于 .

数理统计

定义 112 估计量

给定一个随机变量 密度函数 . 一个估计量(Schätzvariable,Schätzer)是参数 . 一个估计量 是一个无偏估计(erwartungstreu)若 称作估计变量 的偏差(Bias).

定义 113 均方误差MSE

若估计变量 比 有一个小MSE. 那么 就是比 有效率 effizienter.

一个估计变量是在平方中部常数的. 若当 时 .

定义 114 Stichprobenmittel 和 Stichprobenvarianz

样本均值和样本方差

最大似然估计

似然估计函数

定义 115 最大似然估计值

估计值 是对于分布 的参数的最大似然估计值

置信区间(Kondenzintervall)

我们要找2个估计量 ，使得. 其中 是Kondenzniveau置信水平.

由 得出 是标准正态分布. 然后变换成下面的式子 再根据查表和题目条件即可解题

定义 118 分位数

是随机变量，分布为 . 数 使得 是 的 -Quantil

定义 119 正态分布的分位数

对于正态分布 是它的 -Quantil . 我们可以用这个来求置信区间

假设检验

检验的定义

是拒绝域.

是检验集合 中拒绝域中的检验,

是我们要检验的假设Nullhypothese. 是另一个假设 Alternative.

检验的错误

1类错误

满足却被拒绝了 计算是在 的概率里把所有在拒绝域的数量加起来

2类错误

不满足却被接受了 计算就是把在接受区间里的 的概率加起来

1类错误的数量用 来表示. 也叫显著性差异Signifikanzniveau.

二项检验

若是伯努利分布的随机变量，测试某个概率的大小 然后构造测试量, 用正态分布逼近

根据具体情况选择拒绝域的公式

高斯检验

若 服从正态分布

假设

1. gegen ,
2. gegen ,
3. gegen .

检验量 判断拒绝

1. ,
3. .

2次t-检验

若 和 是独立且服从正态分布的随机变量

假设:

1. ，,
2. ，
3. ，

检验量 判断拒绝

1. ,
2. ,
3. .

卡方检验

-Anpassungstest是卡方检验

若: 是独立且相同的随机变量 时可以使用

假设： 检验量： 判断拒绝

随机过程

离散时间处理

定义 123

一个在状态集合 有限的马尔科夫链(Markov-Kette) 由一个无限的随机变量序列 组成. 它的值域是 , 开始分布Startverteilung 是 . 的元素都是非负的且加和为1. 对于下标集合 和任意状态 . 满足： 并且

是转移矩阵,例子

是从 到 走 步走到的概率

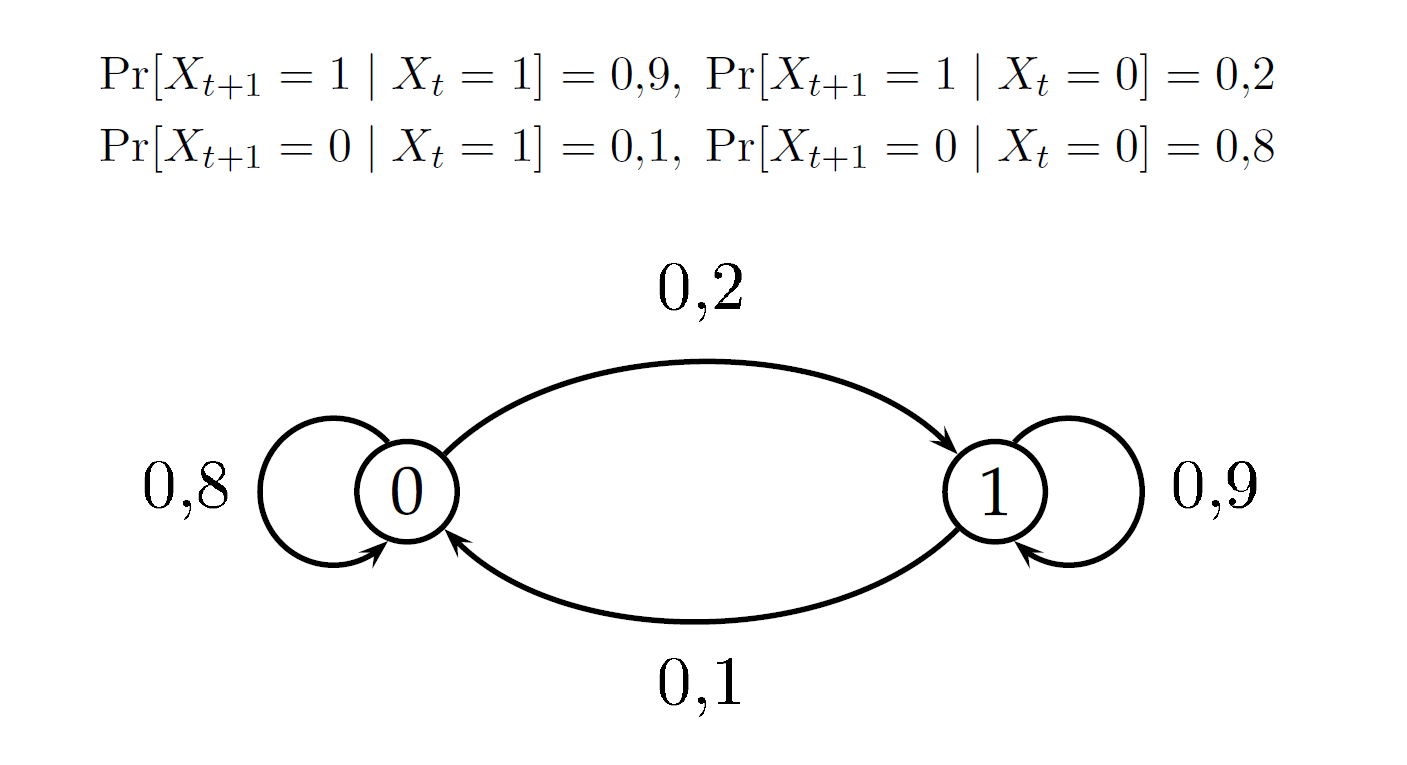
定义 126 步数

随机变量 从 走到 的步数. 是期望. 是从 走到 的概率.

定义 127 到自己的步数

是从 开始又走回来的步数. 同理 是走回来的概率

定理 129 状态转移方程

定义 132 stationäre Verteilung稳定分布

这个分布满足 同时 中加和是 .

定理 134 irreduzibel不可简化的

一个马尔科夫链是不可简化的，若对于所有状态对 存在 使得 .

也就是走几步一定可以到

定理 136 irreduzibel定理

一个不可简化的有限马尔科夫链只有1个稳定分布stationäre Verteilung, 并且满足 für alle

定义 137 Periode周期

一个状态 的 Periode 是最大的数 , 使得 一个状态的 就是非周期性aperiodisch的. 若所有状态是非周期性的aperiodisch，那么这个马尔科夫链是非周期性aperiodisch的

定理138 aperiodisch非周期性

一个状态 是非周期性的aperiodisch, 当且仅当存在 使得对于所有 ， 成立

定义 140 ergodisch可遍历的

不可简化的Irreduzibel 和非周期性 aperiodisch 的马尔科夫链是可遍历的ergodisch

定理 141 Fundamentalsatz für ergodische Markov-Ketten可遍历的马尔可夫链基本定理

对于所有有限的可遍历的ergodisch的马尔科夫链 满足 其中 是唯一的stationäre Verteilung.

​