人工智能
Intelligent Agent
- 通过传感器(sensors)察觉周围环境
- 执行器(actuators)根据环境做出反应
Agents interact with environments through actuators and sensors.
Percept sequence
感知的序列
Agent function
根据感知的序列映射出一个动作
可以选择列表(Tabular Agent Function)或者写程序(Agent Program)。
表格可以在理论上很好的描述(Expressiveness)一个agent的行为,但是缺乏实践意义(Practicality)
Agent program 是agent function的实际实现(practical
implementation)
Rational Agent
理想的agent, 一直做”正确的”事情
- 显然的表现评估法则(performance measure)并不总有
- 设计者需要找到一个可接受的评估法则
对于一个感知序列,一个理想的agent需要选择行动,使得它在给定的知识范围的表现期望最大化
Omniscience agent
知道它行为的最终结果(实际不可能)
Learning学习
Rational agent 可以通过它的感知学习,改进它的知识
Autonomy
一个 rational agent 是autonomous,
如果它相比已经获得的知识,更加依赖于新获得的知识
Task Environment
我们用PEAS来描述
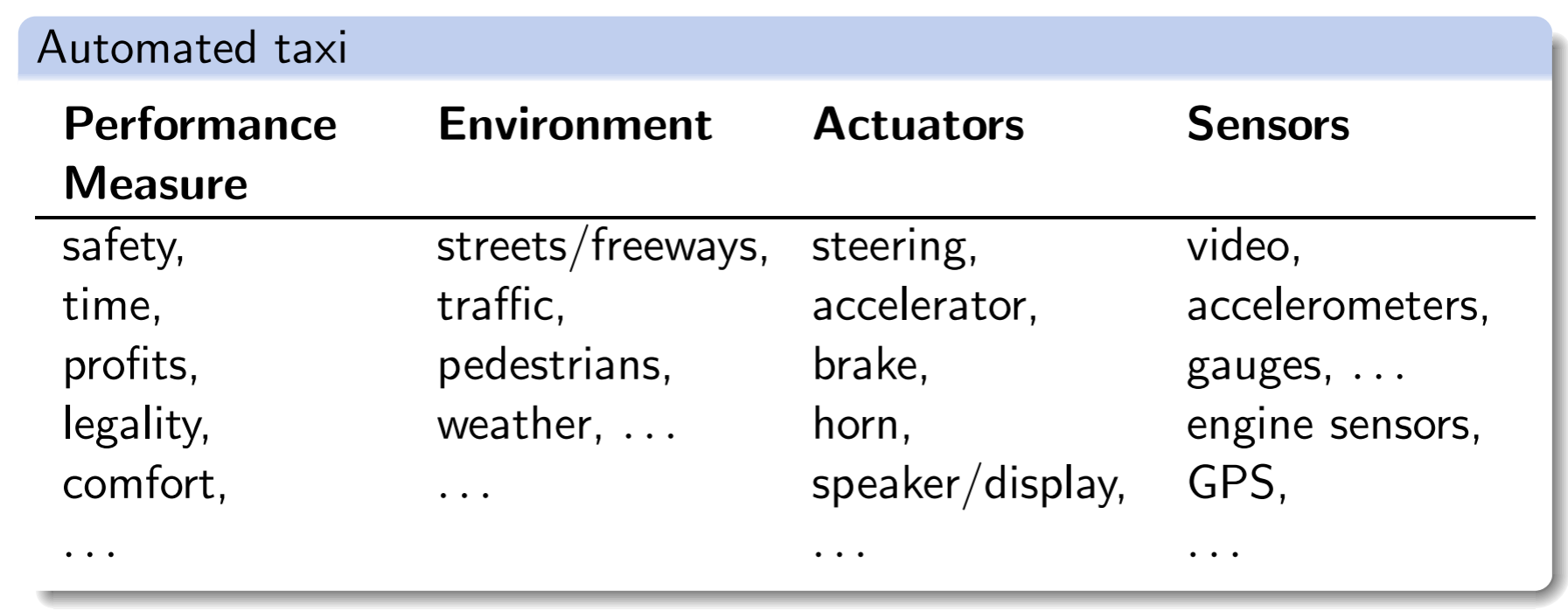 image-20211022153701200
image-20211022153701200
Fully observable/partially
observable
一个环境是可全部观测的,若agent可以检测到环境完整的状态,否则就是部分可观测
Single-agent/multi-agent
一个环境是multi agent环境,若它包含多个agent
Deterministic/stochastic
有确定性若下一个状态完全取决于当前状态
Episodic/sequential
episodic若在一个时期(episode,机器人感知和做出行为的时期)的行为不会影响到下一个时期
discrete/continuous
分为状态的离散/连续和时间的离散/连续
static/dynamic
如果环境的变化只基于agent,那么他是static的
known/unknown
known:如果agent知道行为结果或者结果的概率
Agent Types
- simple reflex agent
- reflex agents with state
- goal-based agents
- utility-based agents
simple reflex agents
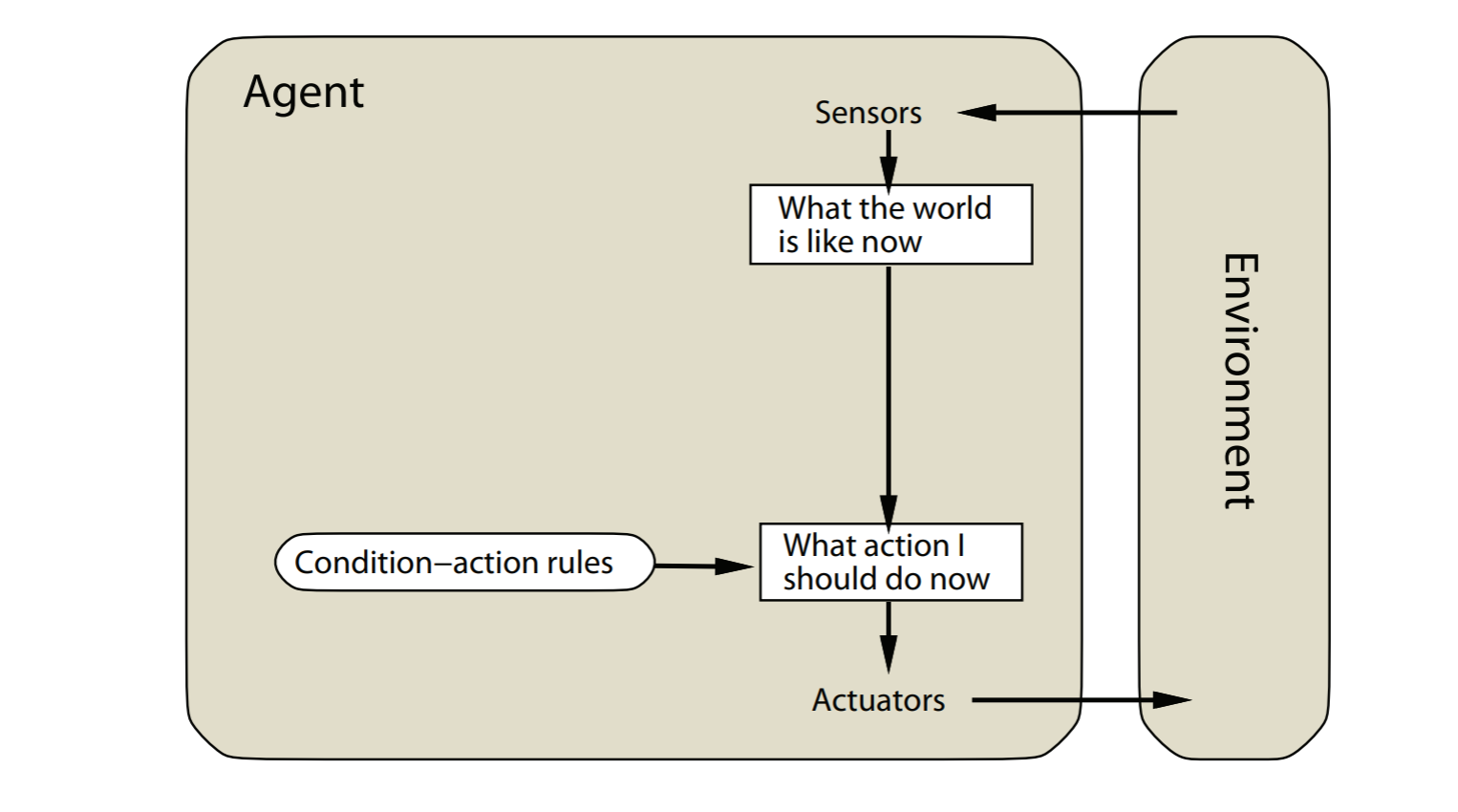 image-20211022154656330
image-20211022154656330
agent的决定基于当前的感知
model-based reflex agents
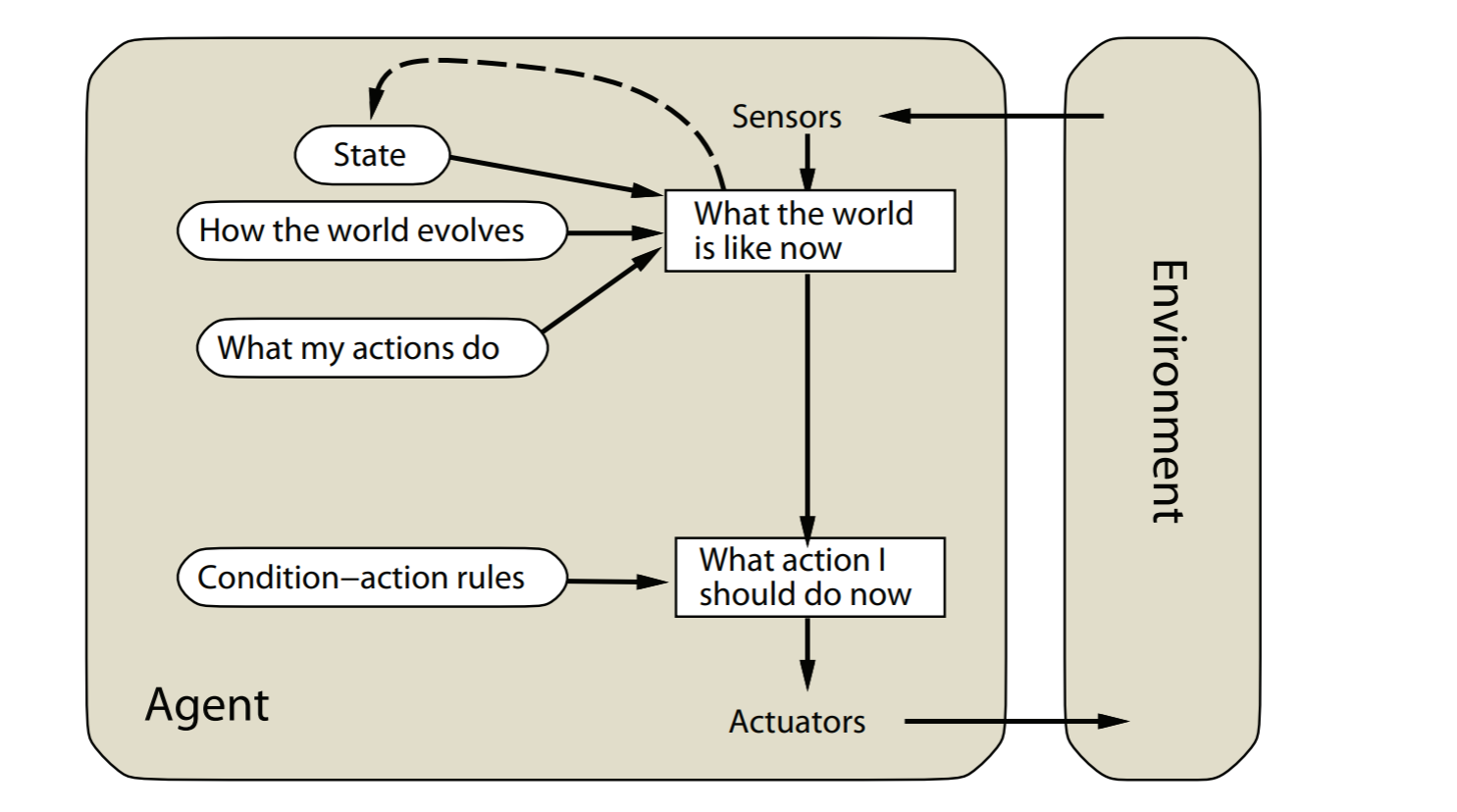 image-20211022154820184
image-20211022154820184
simple reflex agent的扩展版本,可以处理partial observability
通过追踪不能观测的环境
goal-based agents
model-based reflex agents的拓展版本。agent的目标会被explicitly
considered明确的考虑
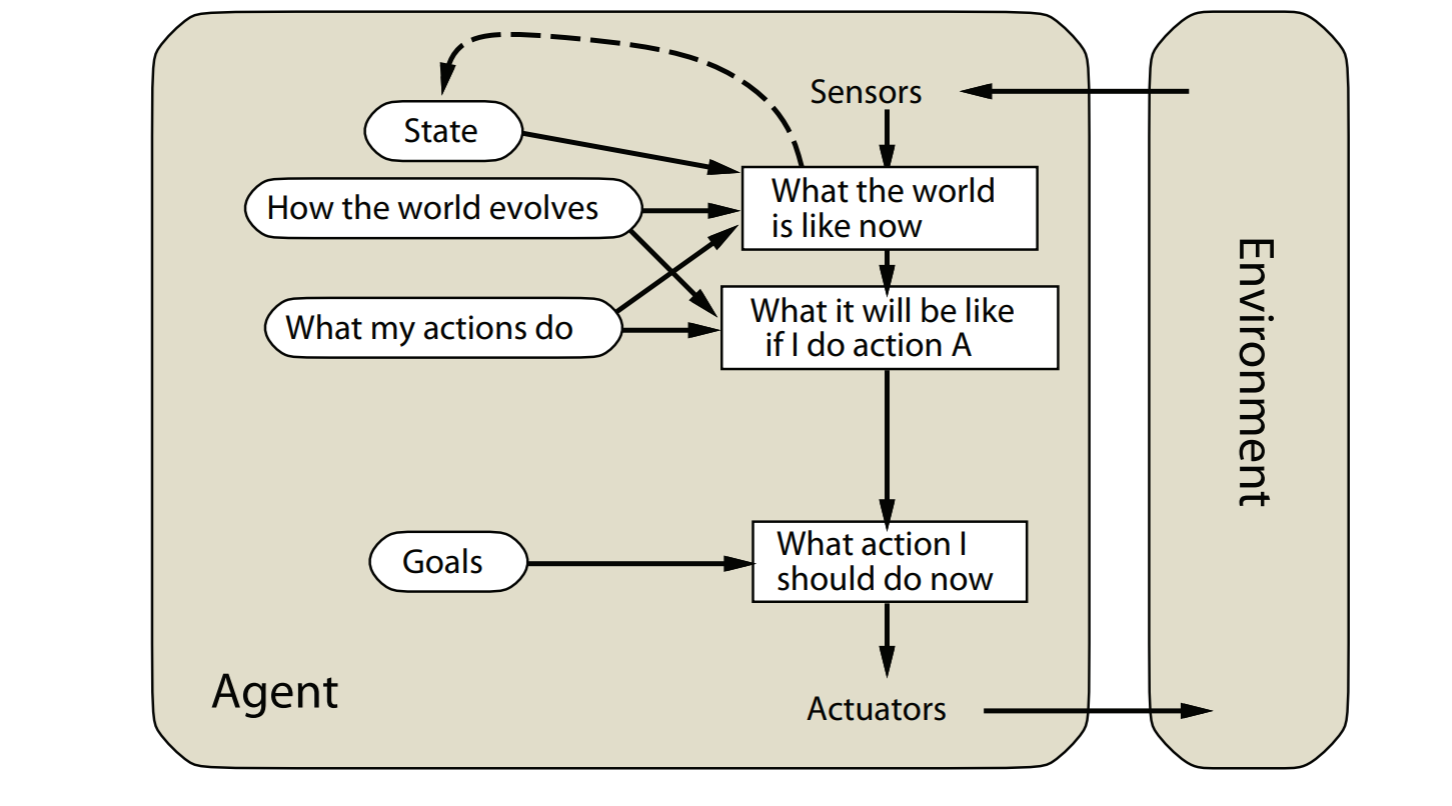 image-20211022155338018
image-20211022155338018
utility-based agents
goal-based reflex agents的扩展版本。
会最大化效用(utility),比如最大化agent的幸福程度
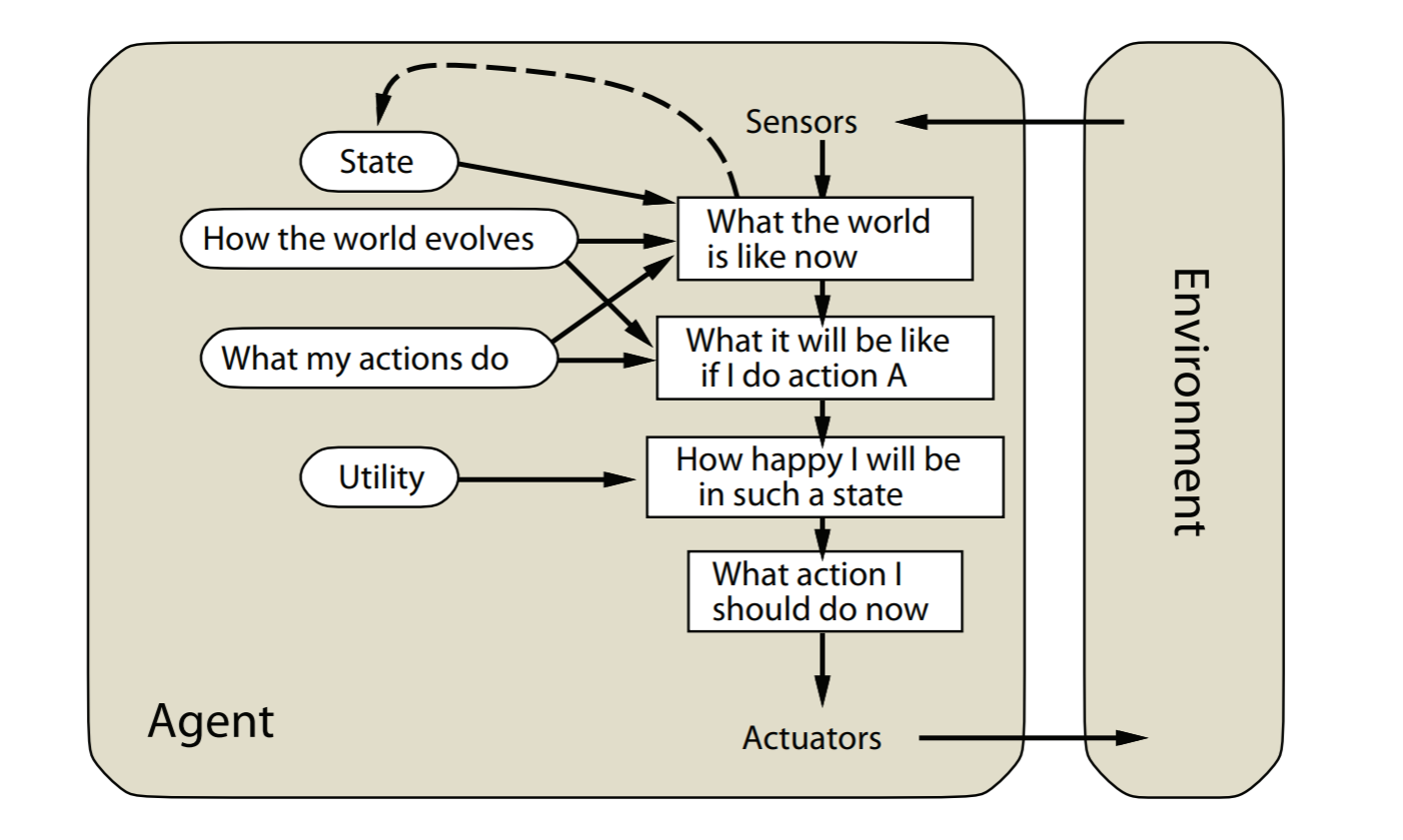 image-20211022155621968
image-20211022155621968
Learning agents
所有agent都可以扩展为学习agent
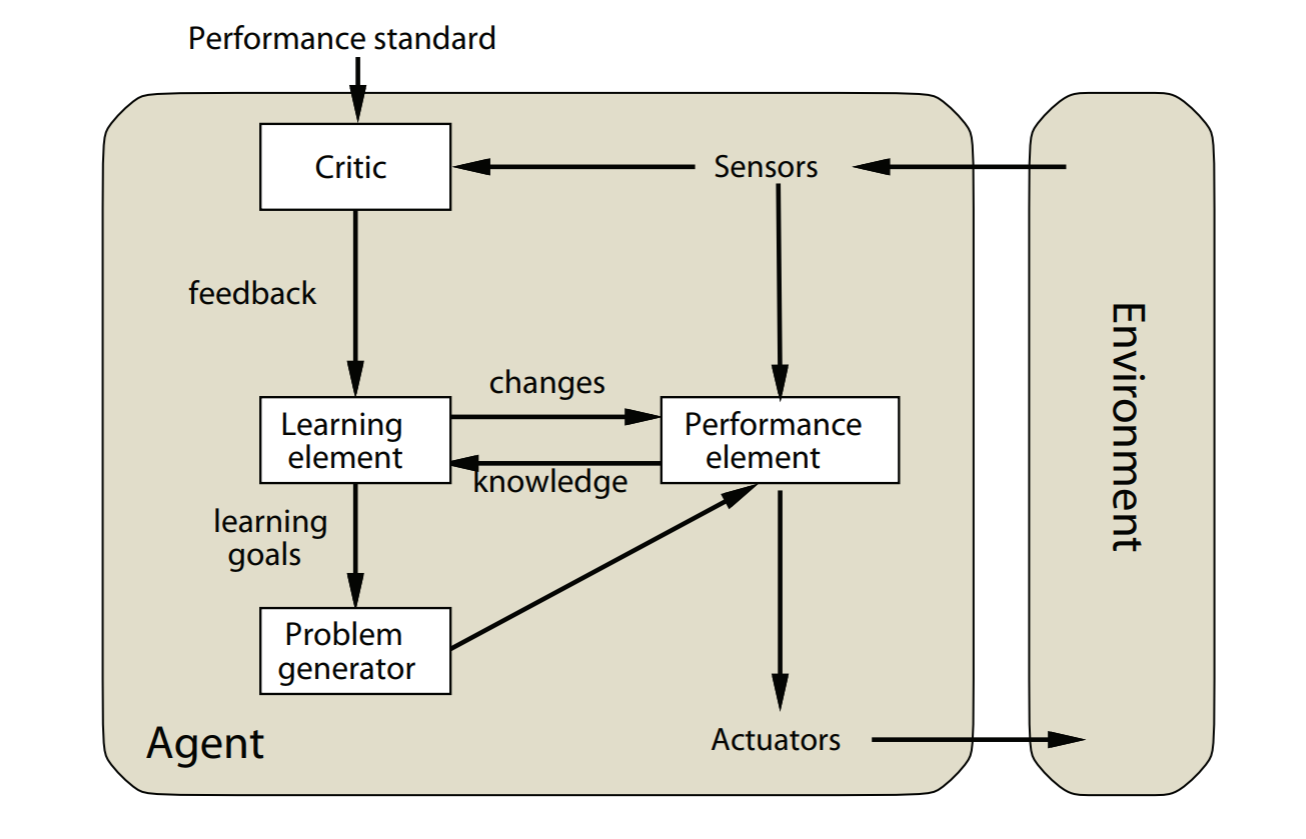 image-20211022155611372
image-20211022155611372
Constraint Satisfaction
Problems
A constraint satisfaction problem is a tuple
是变量集合, 是变量的值域, 是限制的集合
限制的种类
- unary 单个值
- binary 两个变量
- high-order 多个变量
人工智能深度学习
模型评估与选择
经验误差与过拟合
错误率
如果 个样本中有 个错误,则错误率为 ,精度为
误差
学习器在训练集上的误差是训练误差,在新样本上的误差是泛化误差
过拟合和欠拟合
过拟合是学习能力过于强大分类标准过于严格,欠拟合是学习能力低下分类标准过于松
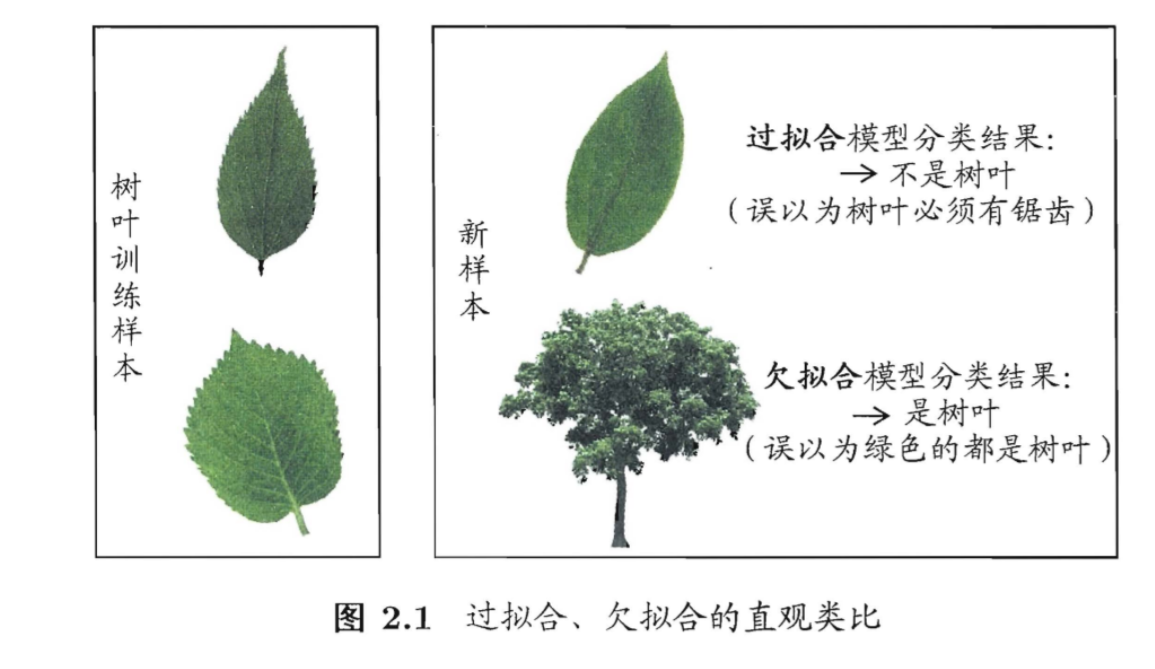 image-20200626134647139
image-20200626134647139
评估方法
我们需要训练集来训练样本,测试集来测试样本。怎样更好地划分出这两个集合呢,有下面这几种办法。
留出法
直接把数据集
分成两个互斥的集合,一个作为训练集
一个作为测试集
。可以直接三七分或者二八分。但是需要注意数据的平均性。
比如有连续的10年内的数据。不能把前7年训练,后三年测试。但这会破坏数据的分布。应该随机抽取7成数据训练,剩下的再测试。
交叉验证法
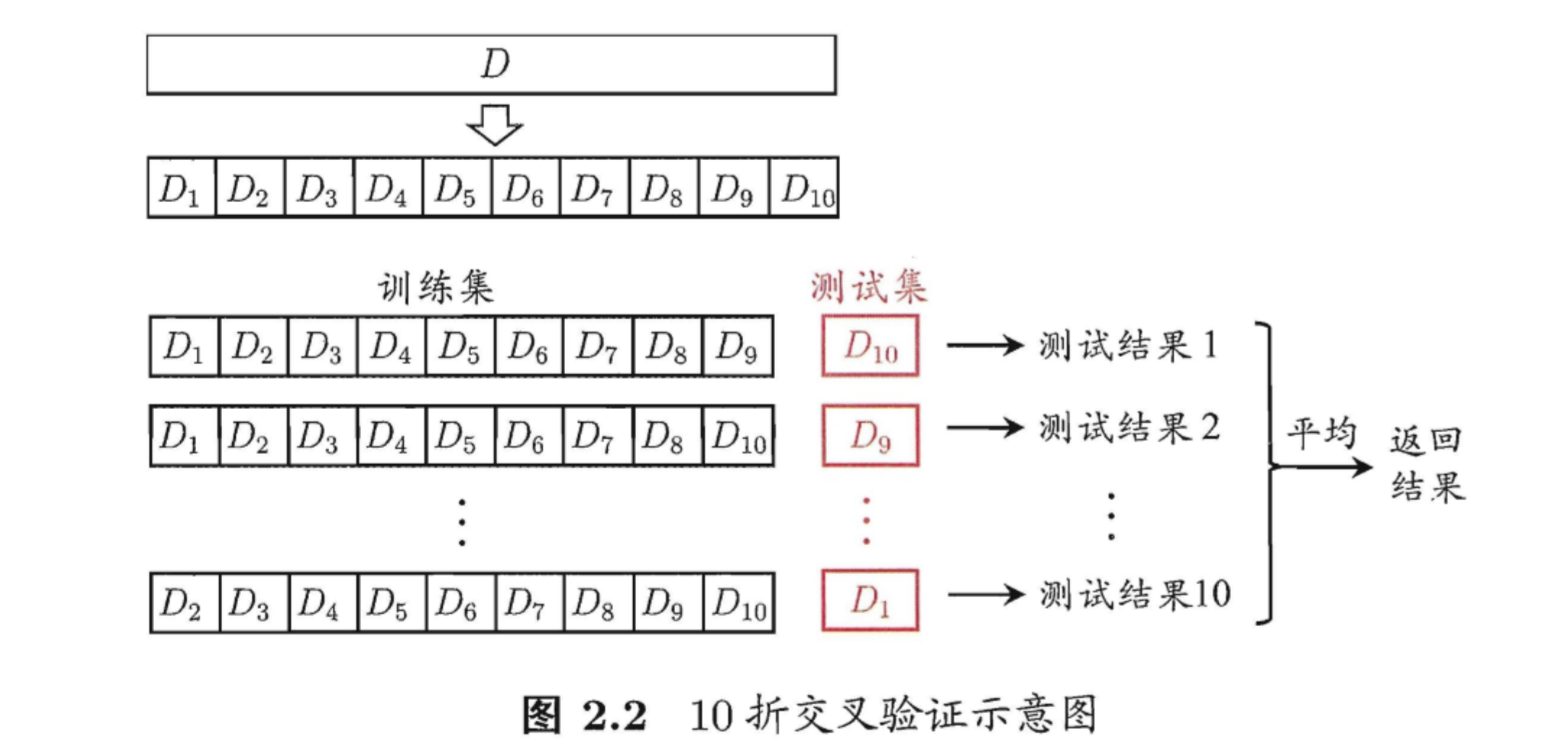 image-20200626141117111
image-20200626141117111
把数据分为10分 到 ,分别
把 到
作为测试集,其他的作为训练集,测试10次。然后取平均值。这对计算机的算力要求高。
自助法
从包含个样本的数据集中每次都随机抽取样本(可以重复),
抽
次,对于每个元素,被抽中的概率是 ,没被抽中的概率是 .所以始终没被选中的概率有
也就是大概的数据没有被选中,可以作为测试集。
调参与最终模型
大多数学习算法都有些参数(parameter)需要设定,参数配置不同,学得模型的性能往往有显著差别.因此,在进行模型评估与选择时,除了要对适用学习算法进行选择,还需调参。
每次选定一个参数,都要重新训练一次。所以我们需要一个验证集来多次验证每一次的训练结果。等调好参数后,最终再用测试集测试最终的结果
性能度量
对学习器的泛化性能进行评估需要有衡量模型泛化能力的评价标准,这就是性能度量。
如果训练集是
回归任务最常用的是均方误差: 对于数据分布
和概率密度函数 ,
它可以描述为 也就是对每个样本出现的概率加权,然后在求和。
错误率和精度
错误率
统计错误个数, 然后除以总个数 这个 是 判断
是否成立,如何是就是 否则就是
.
精度
查准率,查全率与F1
对于2分类问题,正例是答案正确的,反例是答案错误的。是有多少个正确的答案算对了, 是有多少个正确的答案算错了, 是有多少个错误答案算对了。
比如100个数据,70个标答是正确。预测这70个样本中80个是正例,其中正确的是60个,错误的是20个。那么TP就是60,FP就是20,FN就是10
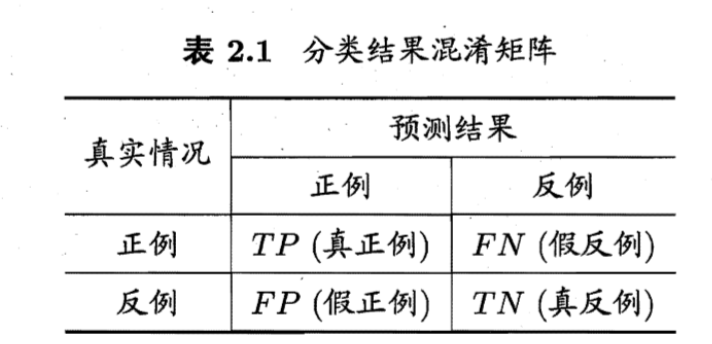 image-20200626144341011
image-20200626144341011
查准率 和查全率 定义为
查准率是我预测出来的正例中的正确率是多少。查全率是所有的样本中我预测出来了多少个正例。
人工智能基础概念
预测
人工智能通上面的公式来预测。w和x是向量,dot是向量积。b是阈值。x是输入。w1是权值,表示每个输入的重要程度。
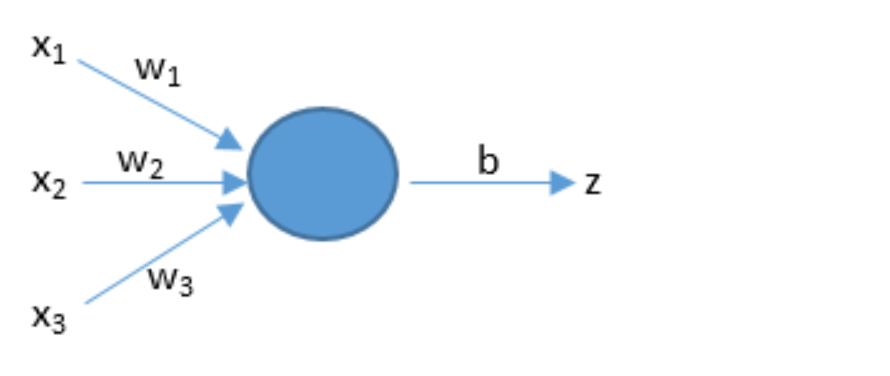 image-20200302204254840
image-20200302204254840
激活函数
在实际的神经网络中,我们不能直接用逻辑回归。必须要在逻辑回归外面再套上一个函数。这个函数我们就称它为激活函数。激活函数非常非常重要,如果没有它,那么神经网络的智商永远高不起来。
我们可以画出它的图像。
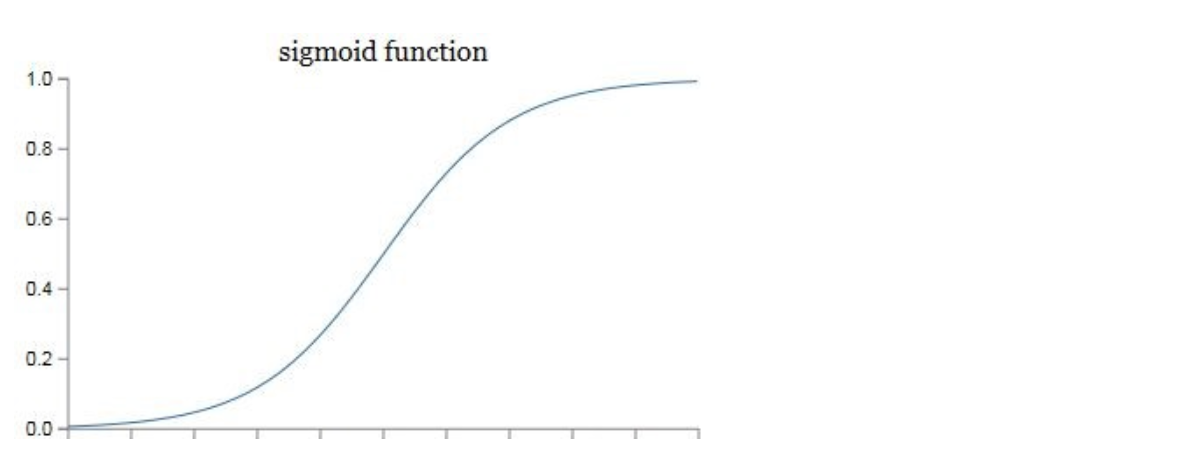 image-20200302204352817
image-20200302204352817
我们在这里先只介绍它的一个用途——把z映射到[0,1]之间。也可以理解为结果的概率
损失函数
神经网络里如何判断自己预测的结果是否准确 在上面的公式中: 表示预测的结果,上面的i表示针对某个训练样本。比如是针对的预测结果。在实践中,我们会用到下面的公式:
但是这只是单个样本的公式,如果我们要堆所有的样本进行精度的预测,那么我们就要用到下面的公式,也就是求和再求平均值
梯度下降
在预测的公式里。w和b决定了预测结果是否准确。所以得到这两个参数的值的方式是梯度下降,它会一步步改变w和b的值,让预测的结果更加精确。上面的公式是一个漏斗型的函数,我们需要求出再函数底部的一组w和b。
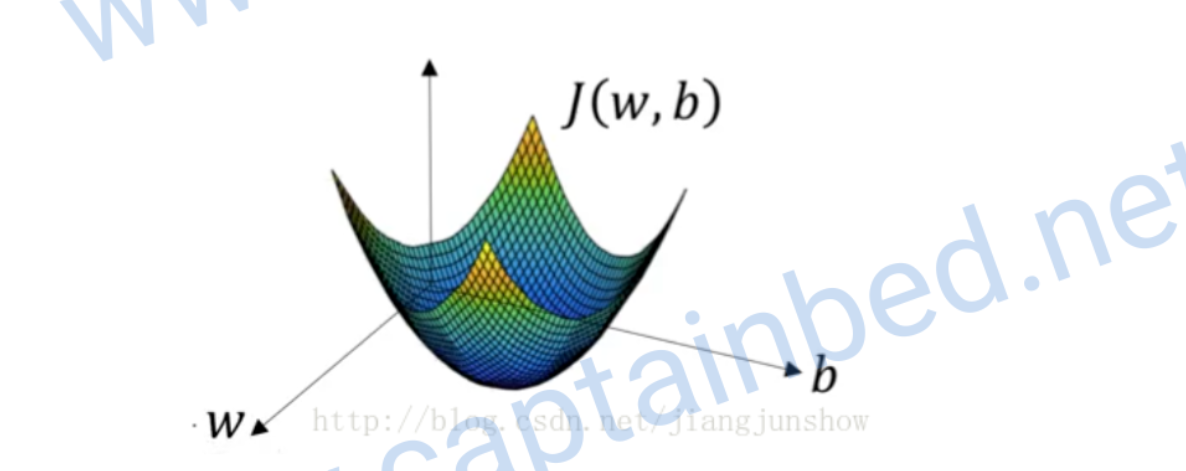 image-20200302205325728
image-20200302205325728
这是一个凸函数(向下凸的函数),我们选择J也是因为它是个凸函数
计算图
计算图是研究人工智能的重要手段。
神经网络的计算是由一个向前传播和一个反向传播构成的。向前传播计算出预测结果和损失。反向传播计算损失函数关于每个参数(w,b)的偏导数来梯度下降。由此往复达到最优的值。
例如:
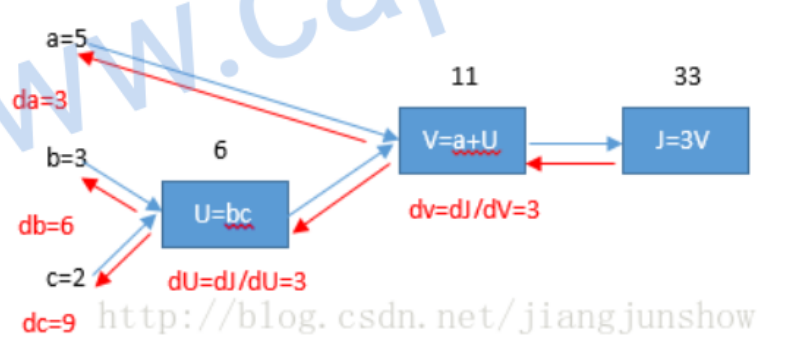 我们可以求出对于的偏导数
我们可以求出对于的偏导数
计算梯度下降的偏导数
例如两个变量的模型,先算出z再算出预测值,然后计算损失函数 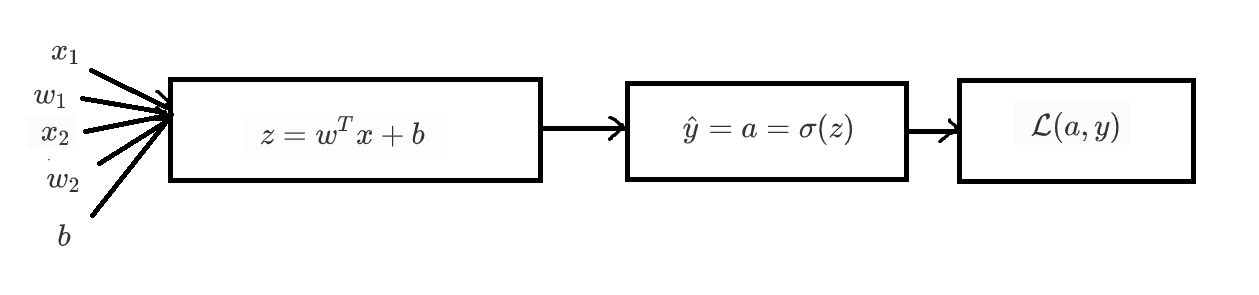
目的是计算出 ,
然后更新
来小损失函数。首先需要计算dL/da和da/dz。dL/da可以直接求导, da/dz需要用到换元法 综上可以算出dL/dz 于是有 得到这三个值之后,就可以利用它们梯度下降
向量化
如果用上面的计算很大的数据,效率是很慢的。我们需要向量化来提速。例如
它等价于
Python环境
Anaconda集成了Jupiter Notebook,是很好的Python开发环境。
链接:https://pan.baidu.com/s/1cTTOBWvLzps1F4XfP875Ig
提取码:050r
下载好后安装完成。打开Anaconda Navigator,点jupyter的launch。
 image-20200305173816371
image-20200305173816371
然后点击右上角的new中的Python3
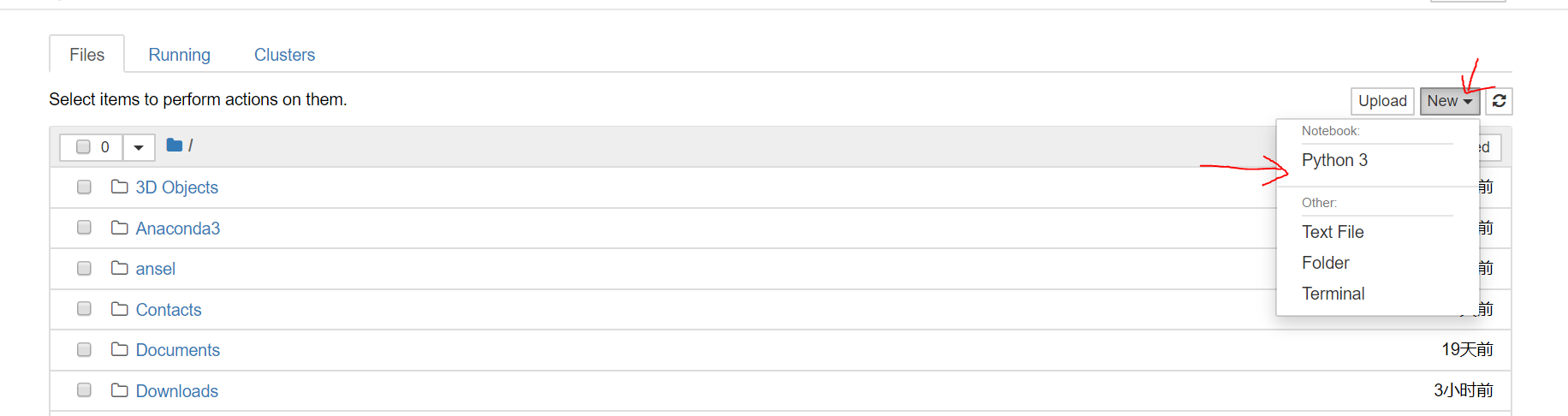 image-20200305173953898
image-20200305173953898
写程序的前置知识
HD5文件
HD5文件。Hierarchical Data
Format(HDF)是一种针对大量数据进行组织和存储的。文件格式,大数据行业和人工智能行业都用它来保存数据。
Python读取HD5文件:
1
2
3
| import h5py
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
|
numpy语法
shape
1
2
| a = np.array([[2,3,3],[2,2,5]])
print(a.shape)
|
reshape
改变数组的规格
1
2
| arr=np.arange(16).reshape(2,8)
print(arr)
|
 image-20200306230719097
image-20200306230719097
1
2
| arr = arr.reshape(4,-1)
print(arr)
|
 image-20200306230804870
image-20200306230804870
T: 转置
1
2
3
| arr=np.arange(16).reshape(2,8)
arr = arr.reshape(8,-1).T
print(arr)
|
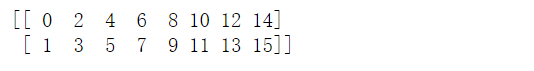 image-20200306231055669
image-20200306231055669
取出列
1
2
3
| print(arr[:, 1])
b = a[:2, :2]
print(b)
|
 image-20200307103625043
image-20200307103625043
交换行列
用切片操作
1
2
|
a[[1,3],:] = a[[3,1],:]
|
初始化
.zero 函数
指数函数exp
1
2
| arr = [0,1,2,4,5,6]
arr = np.exp(arr)
|
求和sum
1
2
3
| arr = np.array([0,1,2,4,5,6])
a = np.array([1,2,4,5,1,2])
arr = np.sum(arr*a)
|
matplotlib
显示图片
1
2
| index =2
plt.imshow(train_set_x_orig[index])
|
或者
1
2
3
|
image = Image.open('images/sample_image.jpg')
plt.imshow(image)
|
Python第一个机器学习的例子
加载库和数据
加载库文件
1
2
3
4
5
| import numpy as np
import matplotlib.pyplot as plt
import h5py
import skimage.transform as tf
%matplotlib inline
|
加载训练和测试数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:])
train_set_y_orig = np.array(train_dataset["train_set_y"][:])
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:])
test_set_y_orig = np.array(test_dataset["test_set_y"][:])
classes = np.array(test_dataset["list_classes"][:])
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
|
预处理
数据扁平化和转置
1
2
| train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
|
全部除以255,使得每个像素点都在 里,方便以后处理
1
2
| train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
|
我们的神经网络图如下
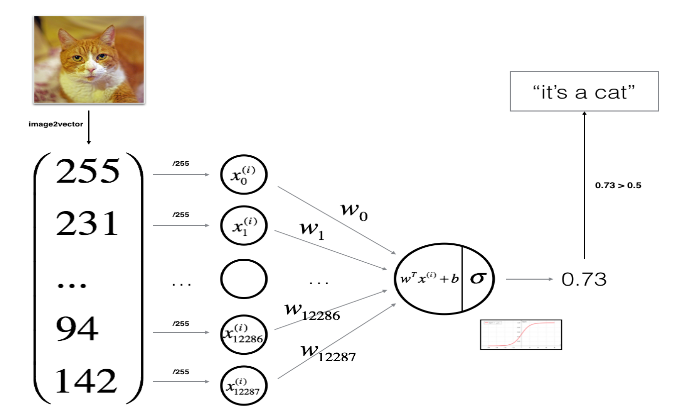 猫
猫
编写工具函数
sigmoid
1
2
| def sigmoid(z):
return 1 / (1 + np.exp(-z))
|
初始化
我们要初始化权重数组w和阈值b, dim是w的大小,在本例中是12288
1
2
3
4
| def initialize_with_zeros(dim):
w = np.zeros((dim,1))
b = 0
return w, b
|
向前传播和反向传播
向前传播: 反向传播:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| def propagate(w, b, X, Y):
"""
参数:
w -- 权重数组,维度是(12288, 1)
b -- 偏置bias
X -- 图片的特征数据,维度是 (12288, 209)
Y -- 图片对应的标签,0或1,0是无猫,1是有猫,维度是(1,209)
返回值:
cost -- 成本
dw -- w的梯度
db -- b的梯度
"""
m = X.shape[1]
A = sigmoid(np.dot(w.T, X) + b)
cost = -np.sum(Y*np.log(A) + (1-Y)*np.log(1-A)) / m
dZ = A - Y
dw = np.dot(X,dZ.T) / m
db = np.sum(dZ) / m
grads = {"dw": dw,
"db": db}
return grads, cost
|
更新w和b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
参数:
w -- 权重数组,维度是 (12288, 1)
b -- 偏置bias
X -- 图片的特征数据,维度是 (12288, 209)
Y -- 图片对应的标签,0或1,0是无猫,1是有猫,维度是(1,209)
num_iterations -- 指定要优化多少次
learning_rate -- 学习步进,是我们用来控制优化步进的参数
print_cost -- 为True时,每优化100次就把成本cost打印出来,以便我们观察成本的变化
返回值:
params -- 优化后的w和b
costs -- 每优化100次,将成本记录下来,成本越小,表示参数越优化
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
if i % 100 == 0:
costs.append(cost)
if print_cost:
print ("优化%i次后成本是: %f" %(i, cost))
params = {"w": w,
"b": b}
return params, costs
|
预测函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| def predict(w, b, X):
'''
参数:
w -- 权重数组,维度是 (12288, 1)
b -- 偏置bias
X -- 图片的特征数据,维度是 (12288, 图片张数)
返回值:
Y_prediction -- 对每张图片的预测结果
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
A = sigmoid(np.dot(w.T, X) + b)
for i in range(A.shape[1]):
if A[0,i] >= 0.5:
Y_prediction[0,i] = 1
return Y_prediction
|
将函数组合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
参数:
X_train -- 训练图片,维度是(12288, 209)
Y_train -- 训练图片对应的标签,维度是 (1, 209)
X_test -- 测试图片,维度是(12288, 50)
Y_test -- 测试图片对应的标签,维度是 (1, 50)
num_iterations -- 需要训练/优化多少次
learning_rate -- 学习步进,是我们用来控制优化步进的参数
print_cost -- 为True时,每优化100次就把成本cost打印出来,以便我们观察成本的变化
返回值:
d -- 返回一些信息
"""
w, b = initialize_with_zeros(X_train.shape[0])
parameters, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
w = parameters["w"]
b = parameters["b"]
Y_prediction_train = predict(w, b, X_train)
Y_prediction_test = predict(w, b, X_test)
print("对训练图片的预测准确率为: {}%".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("对测试图片的预测准确率为: {}%".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
|
浅层神经网络
之前我们学习的是单神经元的神经网络,其实还有多神经元的,比如下面这个
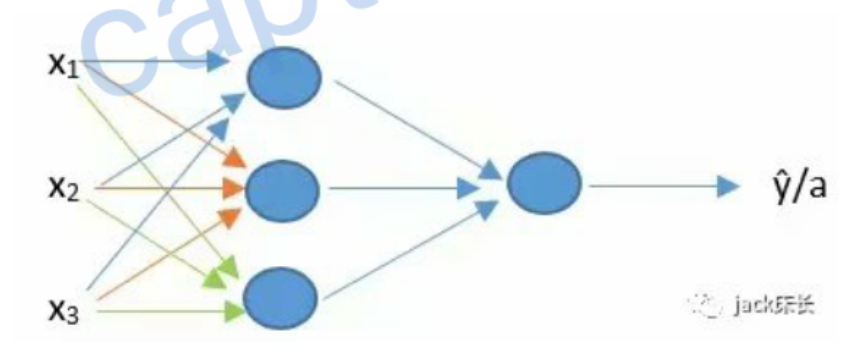
其中的每一个都是单个的神经元
计算向前传播
我们可以先算出第一层神经元的预测值a,上角标表示层数
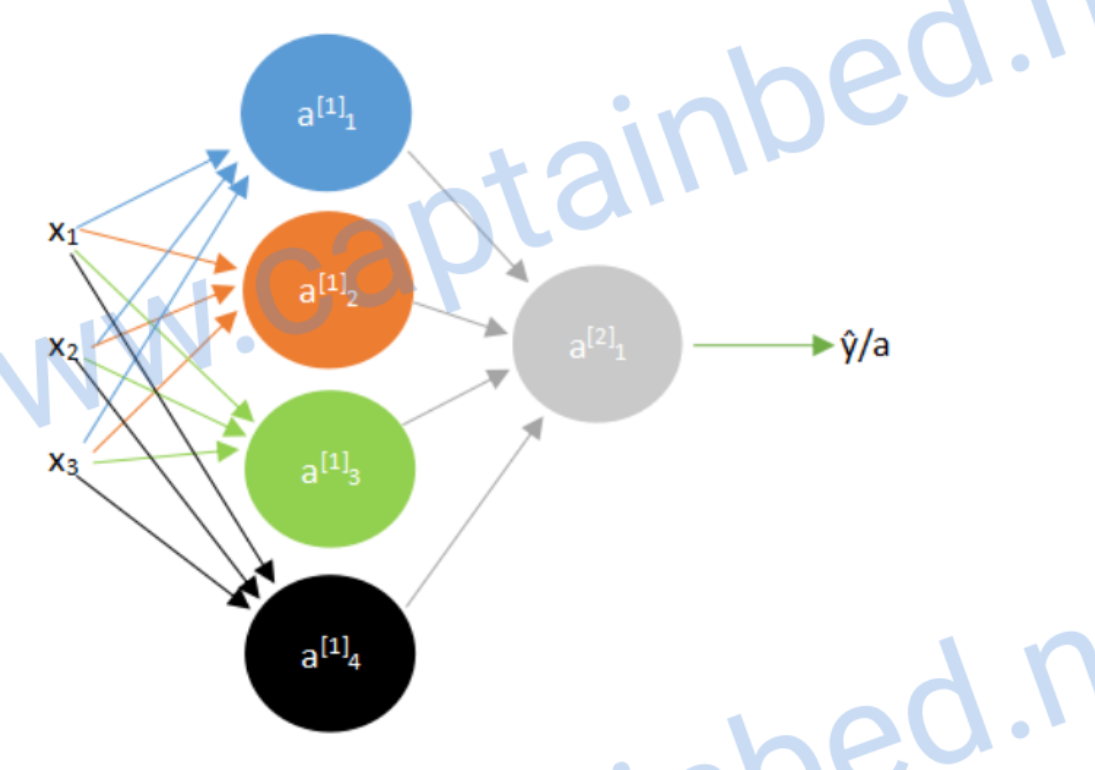 如果有很多神经元,一个个算效率很低,所以我们可以向量化。我们把w值组成一个矩阵
于是我们就可以将上面4个式子简化成1个:
上面的式子只使用于计算单个样本。而我们通常是由多个样本的,我们可以把每组数据的特征值组合成矩阵
于是计算所有样本又可以这样简化:
如果有很多神经元,一个个算效率很低,所以我们可以向量化。我们把w值组成一个矩阵
于是我们就可以将上面4个式子简化成1个:
上面的式子只使用于计算单个样本。而我们通常是由多个样本的,我们可以把每组数据的特征值组合成矩阵
于是计算所有样本又可以这样简化:
计算反向传播
我们先计算出第二层预测值的偏导数
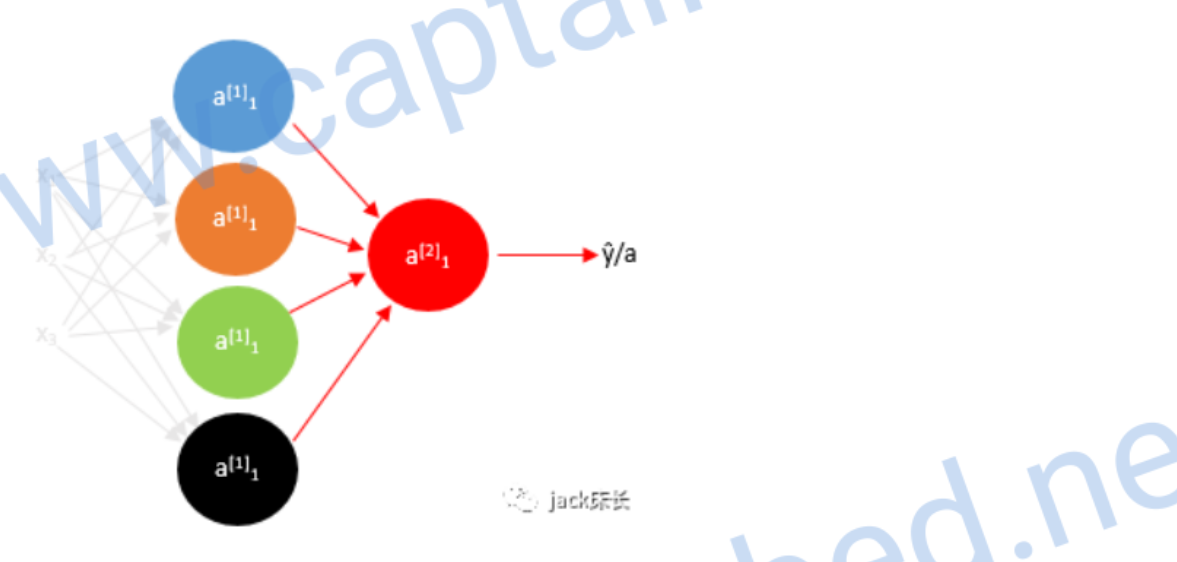 image-20200309195811339
image-20200309195811339
之前我们计算量单神经元的公式: 这个模型和上个单神经元的模型一样,所以我们可以直接套用公式得出
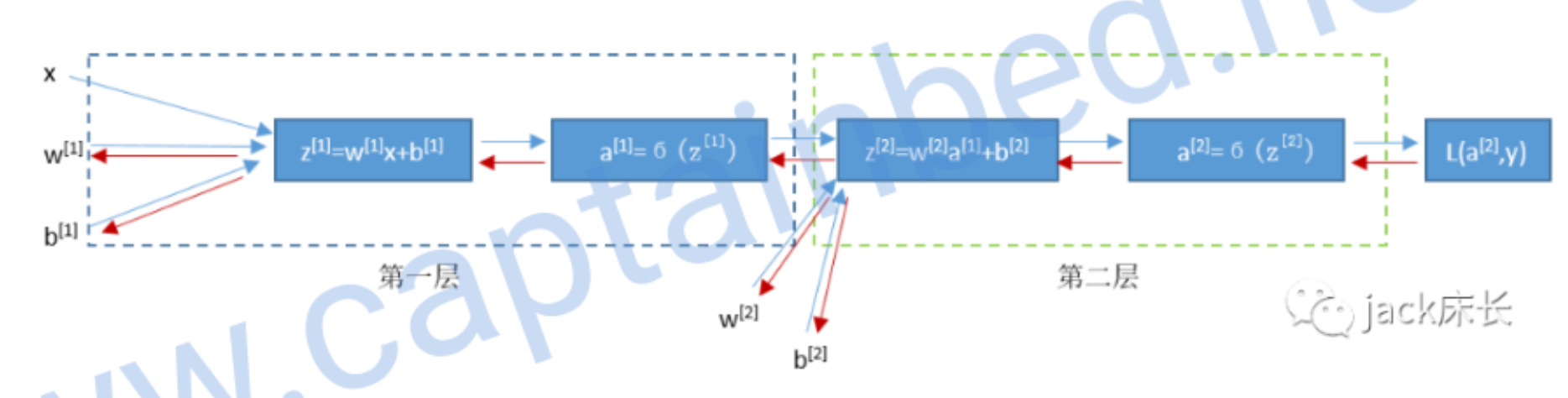
然后我们可以求出
由于激活函数不知有sigmoid,之后我们会具体介绍,我们先用 来表示激活函数
关于 的偏导数 得出 后, 和 就可以通过 算出来: 以上的出来的公式是单样本的公式,多样本的公式如下 最后一行中 axis=1
的作用是让sum只把每一行的加起来,keepdims是保持维度,以免出现 的形式
激活函数
为什么要激活函数?因为我们每一层计算的都是线性的,无法表示复杂情况。就算有多层神经网络也没有用(因为代入之后依然是线性函数)。只有加入了激活函数,才可以表达复杂情况。下面是几种常见的激活函数。
sigmoid
尤其使用于二元分类的问题中,因为0到1的输出值可以表示概率
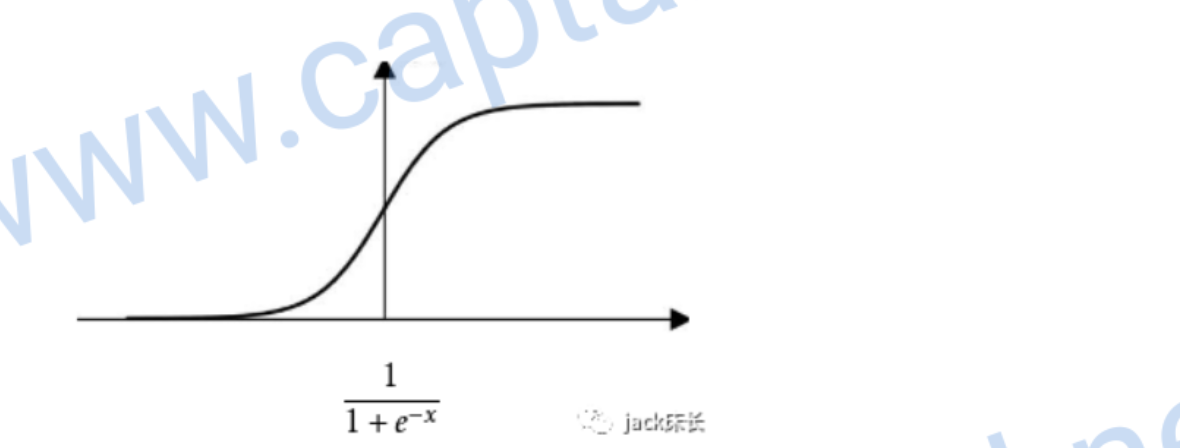 image-20200309220559907
image-20200309220559907
它的偏导数
tanh
它是sigmoid的升级版,各方面都比sigmoid优秀一点
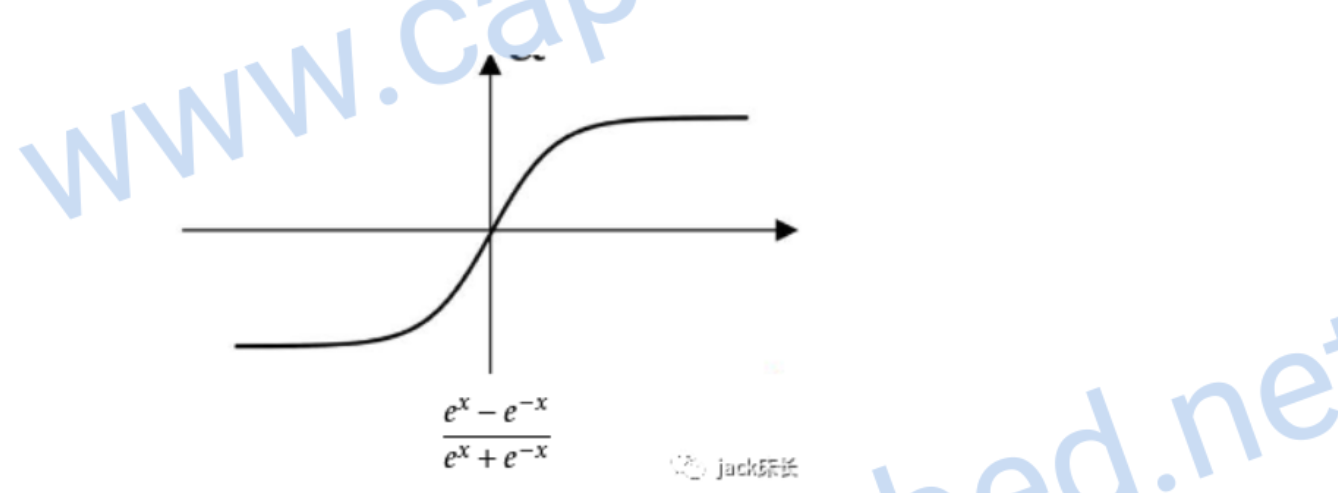 image-20200309220623741
image-20200309220623741
它的偏导数
relu
一般来说,relu用到的最多
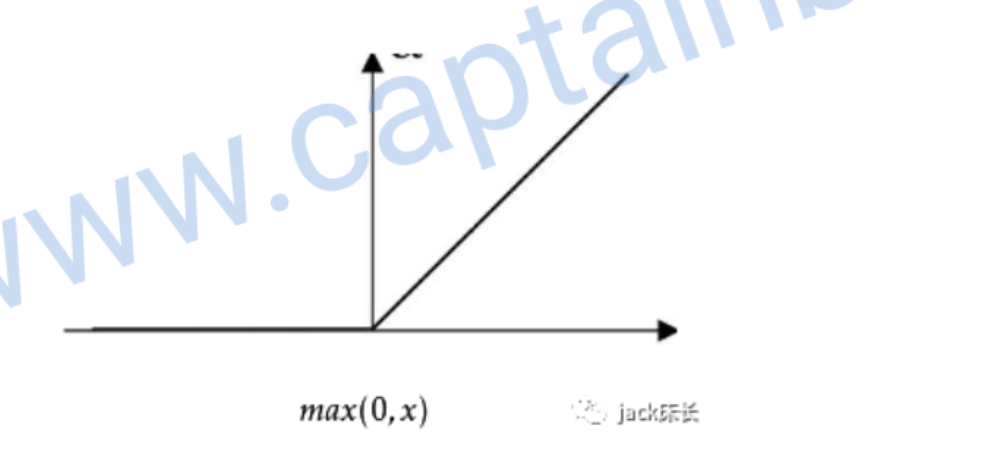 image-20200309220752575
image-20200309220752575
偏导数:
leaky relu
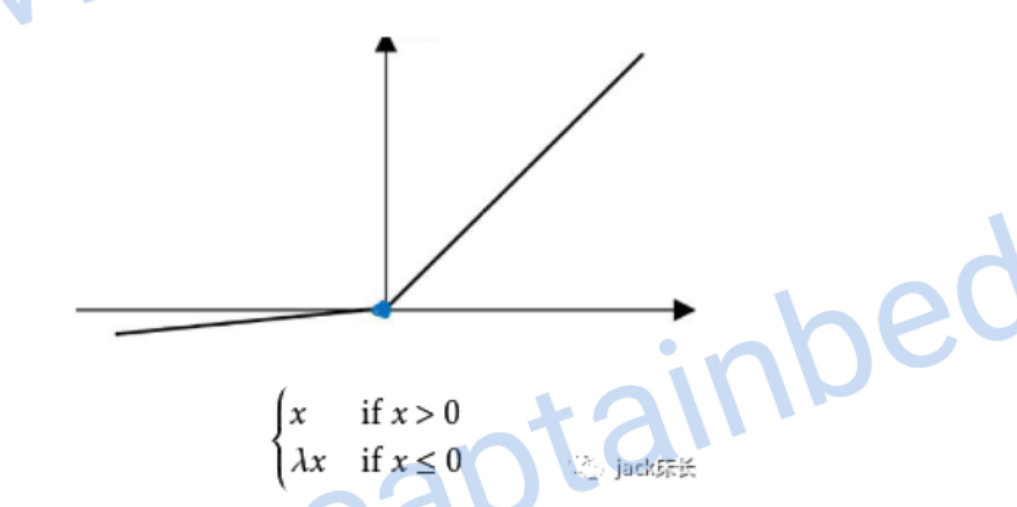 image-20200309221413860
image-20200309221413860
偏导数:
随机初始化参数
对于多层神经网络来说,初始化参数不能都设置成0。否则它就变成了单个神经元。因为输入参数一样,计算结果一样。
一般使用numpy.random.randn来进行随机初始化。
比如
。我们在后面乘0.01的目的是把w变得更加小一点,这样带入sigmod函数里计算出的斜率会大,这样梯度下降的速度就快,神经网络的学习速度就快。
实战编写浅层神经网络
给定一个坐标,判断是蓝色还是红色
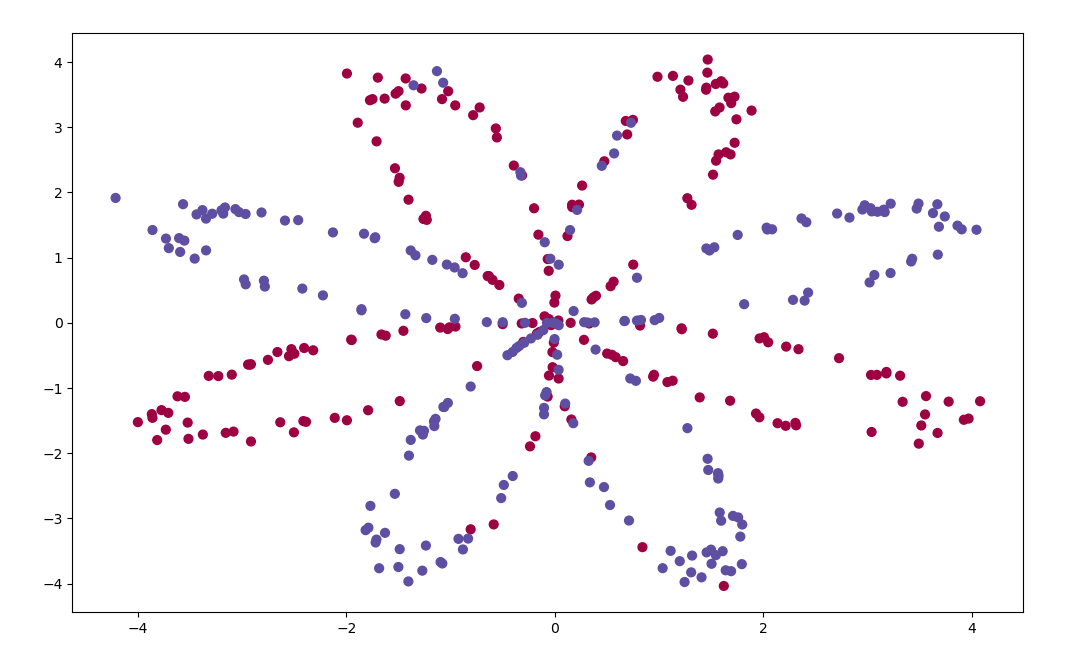 image-20200310095545501
image-20200310095545501
Python知识
ravel扁平化
可以把多维数组压缩成1维数组
1
2
| print(Y.shape, Y.ravel().shape)
|
matplotlib.pyplot.scatter绘制散点
1
2
| plt.scatter(X[0, :], X[1, :], c=Y.ravel(), s=40, cmap=plt.cm.Spectral)
|
例如画一个tanh函数
1
2
3
4
| n = 100
x = np.random.randn(n)
y = np.tanh(x)
plt.scatter(x, y, s=40)
|
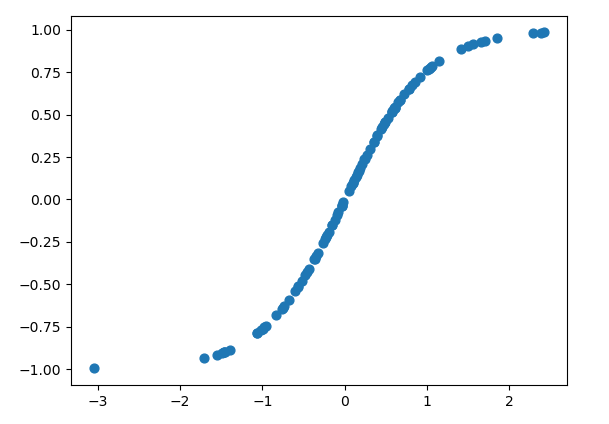 image-20200310102318210
image-20200310102318210
sklearn单神经元学习
1
2
3
| clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T, Y.T.ravel())
LR_predictions = clf.predict(X.T)
|
库文件
这次多了sklearn。它是数据挖掘,数据分析和机器学习的库,里面内置了很多人工智能的函数
1
2
3
4
5
6
7
8
9
10
11
12
13
| import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
from testCases import *
%matplotlib inline
np.random.seed(1)
|
函数
初始化参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| def initialize_parameters(n_x, n_h, n_y):
"""
参数:
n_x -- 输入层的神经元个数
n_h -- 隐藏层的神经元个数
n_y -- 输出层的神经元个数
"""
np.random.seed(2)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
|
向前传播
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| def forward_propagation(X, parameters):
"""
参数:
X -- 输入特征,维度是 (横纵坐标, 样本数)
parameters -- 参数w和b
Returns:
A2 -- The sigmoid output of the second activation
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
|
计算成本函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
def compute_cost(A2, Y, parameters):
"""
参数:
A2 -- 神经网络最后一层的输出结果
Y -- 数据的颜色标签
"""
m = Y.shape[1]
logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
cost = - np.sum(logprobs) / m
return cost
|
反向传播
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| def backward_propagation(parameters, cache, X, Y):
"""
参数:
parameters -- 参数w和b
cache -- 前向传播时保存起来的一些数据
X -- 输入特征
Y -- 标签
"""
m = X.shape[1]
W1 = parameters['W1']
W2 = parameters['W2']
A1 = cache['A1']
A2 = cache['A2']
dZ2= A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
print("W1 dim:" + str(W1.shape))
print("W2 dim:" + str(W2.shape))
print("------------------------------")
print("dZ2 dim:" + str(dZ2.shape))
print("dZ1 dim:" + str(dZ1.shape))
print("------------------------------")
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
|
梯度下降
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
def update_parameters(parameters, grads, learning_rate=1.2):
"""
参数:
parameters -- 参数w和b
grads -- 梯度
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
dW1 = grads['dW1']
db1 = grads['db1']
dW2 = grads['dW2']
db2 = grads['db2']
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
|
把函数组合在一起
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
"""
Arguments:
X -- 输入特征
Y -- 标签
n_h -- 隐藏层的神经元个数
num_iterations -- 训练多少次
print_cost -- 是否打印出成本
"""
np.random.seed(3)
n_x = X.shape[0]
n_y = Y.shape[0]
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
for i in range(0, num_iterations):
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2, Y, parameters)
grads = backward_propagation(parameters, cache, X, Y)
parameters = update_parameters(parameters, grads)
if print_cost and i % 1000 == 0:
print ("在训练%i次后,成本是: %f" % (i, cost))
return parameters
|
预测新数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
def predict(parameters, X):
"""
参数:
parameters -- 训练得出的参数(学习到的参数)
X -- 预测数据
"""
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2)
return predictions
|
评估
1
2
3
4
5
6
7
8
9
10
11
12
|
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)
predictions = predict(parameters, X)
print ('预测准确率是: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y.ravel())
|
深层神经网络
浅层神经网络只有两层。而深层神经网络可以由任意层。简单来说,就是把上一层的结果作为下一层的输入。
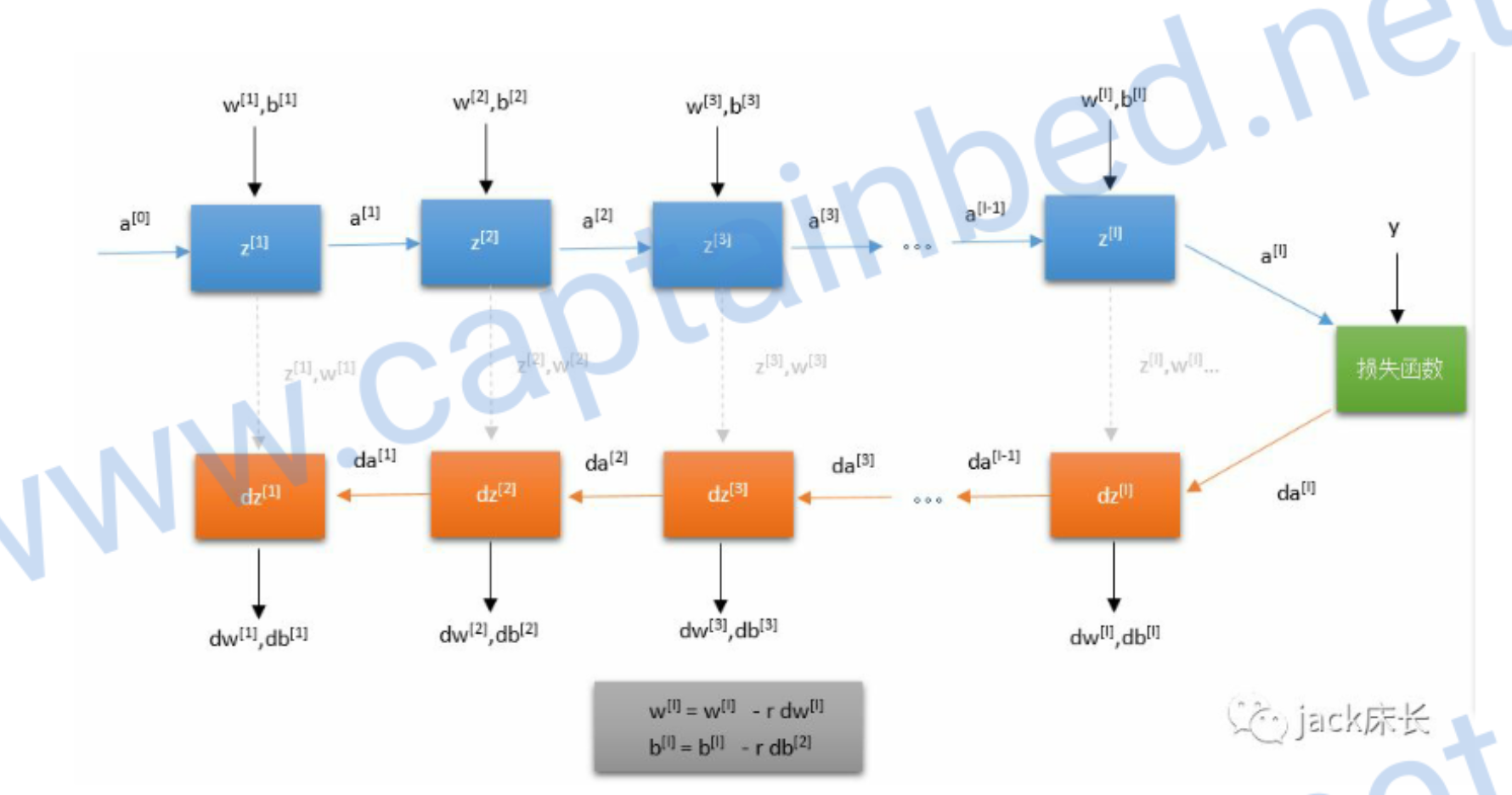 image-20200329180212175
image-20200329180212175
核对矩阵的维度
编写程序的时候,我们很容易由于维度的错误而出现错误。比如下面这张图。
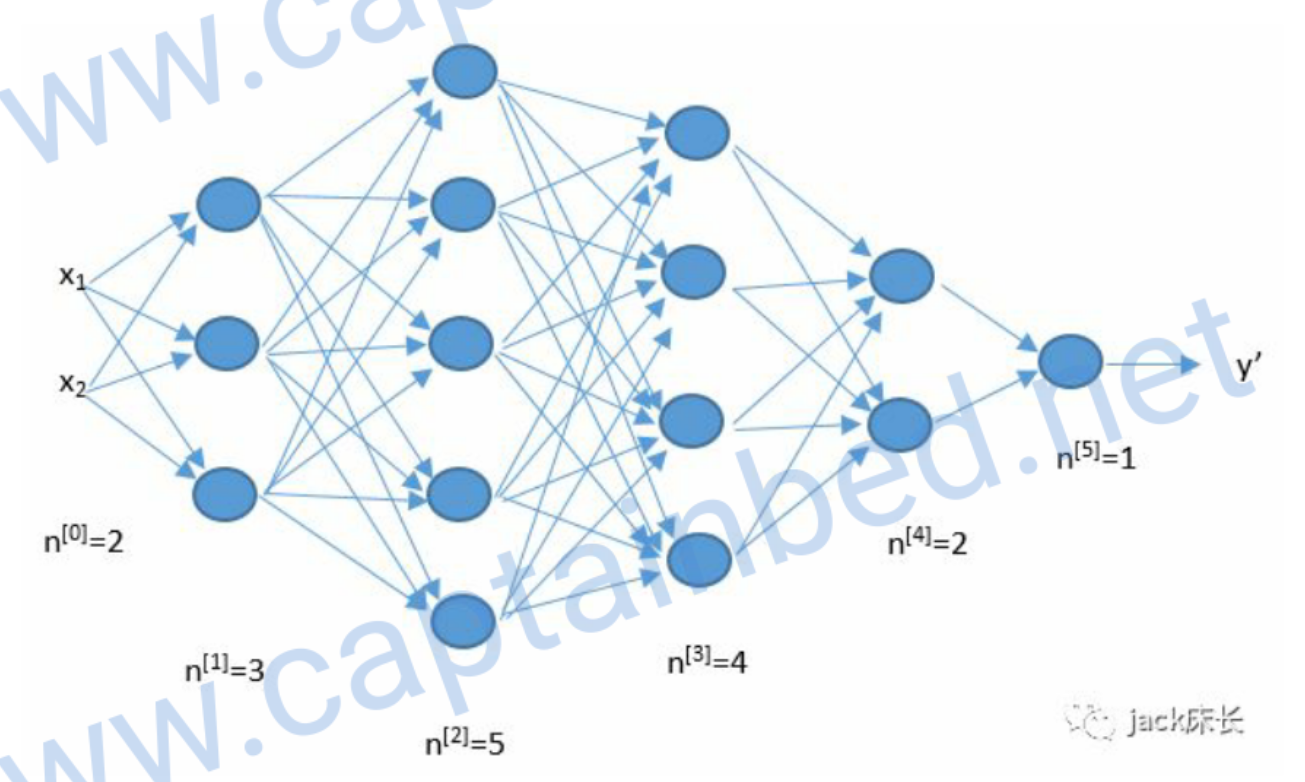 image-20200329180639884
image-20200329180639884
输入层有2个元素,所以