高效算法II

线性规划(LP)

Standard Form

input: number $a_{ij},c_j,b_j$

output: numbers $x_j$

$n = \#decision variables, m=\#conatrains$

$\begin{aligned} & \max \sum_{j=1}^n c_j x_j \\ & \text { s.t. } \sum_{j=1}^n a_{i j} x_j=b_i \quad 1 \leq i \leq m \\ & x_j \geq 0 \quad 1 \leq j \leq n \\ & \end{aligned}$

也可以用矩阵的写法

$\begin{array}{rr}\max & c^T x \\ \text { s.t. } \quad A x=b \\ & x \geq 0\end{array}$

转换成Standard Form

小于等于

$a-3b+5c\le 12$ 变成 $a-3b+5c+s=12,s \ge 0$
大于等于

$a-3b+5c\ge 12$ 变成 $a-3b+5c-s=12,s \ge 0$
min to max:

$\min a-3b+5c$ 变成 $\max -a+4b-5c$

我们也可以从 Standard Form 变成小于等于或者大于等于

$a-3b+5c=12$ 变成

$a-3b+5c\le 12$
$-a+3b-5c\le12$

如果 $x$ 要求无限制

$x=x^+-x^-,x^+\ge0,x^-\ge0$

定义1 线性规划(LP)

设 $A \in \mathbb{Q}^{m \times n}, b \in \mathbb{Q}^m, c \in \mathbb{Q}^n, \alpha \in \mathbb{Q}$ , 是否存在 $x \in \mathbb{Q}^n$ 使得 $A x=b, x \geq 0, c^T x \geq \alpha$

插入一段复习：

NP问题和co-NP问题:

Given a solution to an NP problem, the "yes" solution can be verified in polynomial time.

A problem is in co-NP if its "no" instances can be verified in polynomial time.

一般问题要么是P要么是NP-complete, 而NP和co-NP的交集是包含P不包含NP-complete的

有下列问题

Is LP in NP?

answer

Yes. 因为给定 $B$ 我们可以计算 associated basic solution $A_B^{-1} b$ 在多项式复杂度. 答案肯定是有理数，不是无理数.
Is LP in co-NP?

answer

Yes. 因为反例也可以快速代入验证
Is LP in P?

answer

Yes.

一些基本定义

对于一个Standard Form 的 LP: $P=\{x \mid A x=b, x \geq 0\}$

$P$ 是 feasible region
A point $x\in P$ is feasible point
若 $P\ne \emptyset$ 那么 LP 是 feasible的，否则就 infeasible
LP 是 bounded 若它是feasible且答案不会到无穷大

定义2 linear combination

对于vector $x_1, \ldots, x_k \in \mathbb{R}^n, \sum \lambda_i x_i$ 是

linear combination, 若 $\lambda_i \in \mathbb{R}$
affine combination, 若 $\lambda_i \in \mathbb{R}, \sum_i \lambda_i = 1$，是直线
convex combination, 若 $\lambda_i \in \mathbb{R}, \sum_i \lambda_i = 1, \lambda_i \ge 0$，是线段
conic combination, 若 $\lambda_i \in \mathbb{R}, \lambda_i \ge 0$, 是一个cone

可以画图理解它们

定义3 Linear space

集合 $X ^n $

linear space 若 closed under linear combination
affine space 若 closed under affine combination
convex 若 closed under convex combination
convex cone 若 closed under conic combination

注意，affine space 不是 vector space

定义4 span

对于 $X \in \mathbb{R}^n$

$span(X)$ 是 $X$ 中 linear combination 的集合 (linear hull)
$aff(X)$是 $X$ 中 affine combination 的集合 (affine hull)
$conv(X)$是 $X$ 中 convex combination 的集合 (convex hull)
$cone(X)$是 $X$ 中 conic combination 的集合 (coinc hull)

定义 5 convex function

一个函数 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 是 convex 若对于 $x,y\in \mathbb{R}^n$ 和 $\lambda \in [0,1]$ 有

\[ f(\lambda x+(1-\lambda) y) \leq \lambda f(x)+(1-\lambda) f(y) \]

Lemma 6 convex P

若 $P\subseteq \mathbb{R}^n$ 且 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 是convex，那么下面也是

\[ Q=\{x \in P \mid f(x) \leq t\} \]

?

定义 7 affine subspace

affine subspace $A$ 的 $\dim(A)$ 是 vector space $\{x-a|x\in A\}$ 的维度

定义 8 convex set

convex set $X$ 的 $\dim(X)$ 是它的 affine hull $aff(X)$ 的维度

定义 9 hyperplane

集合 $H\subseteq \mathbb{R}^n$ 是 hyperplane 若 $H=\left\{x \mid a^T x=b\right\}$, for $a \neq 0$.

定义 10 halfspace

集合 $H'\subseteq \mathbb{R}^n$ 是 (closed) halfspace 若 if $H=\left\{x \mid a^T x \leq b\right\}$, for $a\ne 0$.

定义 11 polytop

Polytop $P\subseteq \mathbb{R}^n$ 是有限点的 convex hull 的集合 $P = conv(X)$

定义 12 Polyhedron

Polyhedron是有限 half-spaces 的交集 $\left\{H\left(a_1, b_1\right), \ldots, H\left(a_m, b_m\right)\right\}$ 其中，

\[ H\left(a_i, b_i\right)=\left\{x \in \mathbb{R}^n \mid a_i x \leq b_i\right\} \]

定义 13 Bounded Polyhedron

一个 Polyhedron 是 bounded 若存在 $B$ 使得 $\forall x\in P. \|x\|_2 \leq B$

定理 14 polytop and polyhedron

$P$ is a bounded polyhedron iff $P$ is a Polytop.

?

定义 15 supporting hyperplane

设 $P\subseteq \mathbb{R}^n,a\in \mathbb{R}^n,b\in \mathbb{R}$ 那么 hyperplane

\[ H(a, b)=\left\{x \in \mathbb{R}^n \mid a^T x=b\right\} \]

是 $P$ 的 supporting hyperplane 若 $\max \left\{a^T x \mid x \in P\right\}=b$

如果不是的话, $\max{a^Tx}$ 要么小于 $b$ 要么大于 $b$ 不会等于 $b$

定义 16 Face

设 $P\subseteq \mathbb{R}^n$ $F$ 是 $P$ 的 face 若 $F=P $ 或者 $F = P\cap H$ 对于某些 hyperplane $H$

边界上的一部分

设 $P\subseteq \mathbb{R}^n$

a face $v$ is vertex 若 $\{v\}$ 是 $P$ 的 face
a face $e$ is an edge 若 $e$ is face and $\dim(e)=1$
a face $F$ is a facet 若 $F$ is face and $\dim(F)=\dim(P)-1$

定义 18 等价定义 vertex

给定 polyhedron $P$. 点 $x\in P$ 是 vetex 若存在 $c\in \mathbb{R}^n$ 使得对于 $\forall y\in P,y\ne x$ 有 $c^T y<c^T x$

c 是 hyperplane

定义 19 extreme point

给定 polyhedron $P$. 点 $x\in P$ 是 extreme point 若 $\nexists a, b \neq x, a, b \in P$, with $\lambda a+(1-\lambda) b=x$ for $\lambda \in[0,1]$.

不存在 a,b 把 x 夹在中间

Lemma 20 vertex and extreme point

A vertex is also an extreme point

Observation

The feasible region of an LP is a Polyhedron.

Convex Set

定理 21 答案在端点

若存在LP的最优解，那么存在一个最优解是extreme point.

不存在最优解的情况是 infeasible 或者答案无穷大

证明

假设 $x$ 是最优解但不是extreme point,那么存在一个方向 $d$ 使得 $x \pm d \in P$ (Definition 19) 然后由于$A(x \pm d)=b$ (feasible 满足LP定义) 通过两个方程加减得到 $Ad=0$. 不妨假设 $c^T d \geq 0$ (如果是负数就换一个方向)

Case 1 $ j.$ s.t. $d_j<0$ 存在某一列是小于0的

增加 $\lambda$ 到 $\lambda '$ 使得第一个 $x+\lambda d$ 的某一项到0. 因为$x+\lambda' d$ 是 feasible 所以$A\left(x+\lambda^{\prime} d\right)=b, x+\lambda^{\prime} d \ge 0$ 所以 $c^T x^{\prime}=c^T\left(x+\lambda^{\prime} d\right)=c^T x+\lambda^{\prime} c^T d \geq c^T x$ 其中 $\lambda '>0$ 是移动的步长, $c^Td\ge 0$ 根据假设.
Case 2. $d_j \ge 0$ 且 $c^Td>0$

因为如果 $c^Td=0$ 那么我们可以换一个 $d$ 的方向，这样可以归到Case1里面. 然后 $x+\lambda d$ 是 feasible 的因为 $A(x+\lambda d)=Ax+\lambda Ad=Ax=b$ 所以只要$x+\lambda d \ge 0$ 就能 feasible.

所以我们可以把 $\lambda$ 变成无穷大, 因为$c^T d>0$ 所以 $c^T(x+\lambda d) \rightarrow \infty$ 答案就变成无穷大了.

记号 Submatrix

设 $B \subseteq\{1 \ldots n\}$ 是列的下标集合，那么定义 $A_B$ 是 $A$ 的所有 $B$ 中列的子集矩阵.

定理 22 extreme point

设 $P=\{x \mid A x=b, x \geq 0\}$ 对于 $x\in P$ 设 $B=\left\{j \mid x_j>0\right\}$ 那么 $x$ 是 extreme point iff $A_B$ 有 linearly independent columns.

Recap1: 测试 independent vectors $v_1,v_2...$ 就是把他们列在一起，解方程 $v_1x_1+v_2x_2..=0$ 的解是否是 $x_i=0$ 是就是 independent. 也即是 $Ax=0$ 的解是否是 $x=0$, 其中 $A$ 是这些向量的列组成的矩阵

Recap2: $Ax = v_1 x_1+v_2x_2+...$ 其中 $v_i$ 是列

证明

($\Leftarrow$)

设 $x$ 不是extreme point. 那么存在方向 $d$ 使得 $x \pm d \in P$ 于是 $Ad=0$ 然后我们定义 $B^{\prime}=\left\{j \mid d_j \neq 0\right\}$ 那么 $A_{B'}$ 有 linearly dependent column 因为 $Ad=0$ . 因为 $d_j=0$ 的列不影响 $Ad$ 的计算结果. 如果 $x_j=0$那么有$d_j=0$，因为如果$d_j\ne 0$ 那么可以改变方向使得 $x_j$ infeasible而我们假设存在这个方向 $d$ 是feasible的. 由于 $B' \subseteq B$ 所有 $A_B$ 是dependent的

($\Rightarrow$)

若 $A_B$ 有dependent column那么 $\exists d\ne 0. A_Bd=0$ 于是扩展 $d$ 到 $\mathbb{R}^n$ 当 $x_j=0$ 的时候 $d_j=0$ 那么对于足够小的 $\lambda$ 我们有 $x \pm \lambda d \in P$ 所以 $x$ 不是 extreme point.

定理 23 vertex

设 $P=\{x \mid A x=b, x \geq 0\}$ 设点 $x \in P$ 设 $B=\left\{j \mid x_j>0\right\}$ $A_B $ 有 independent column (extreme point) 那么 $x$ 是 vertex.

证明

构造一个hyperplane $c_j= \begin{cases}0 & j \in B \\ -1 & j \notin B\end{cases}$ 所以 $c^T x=0$ 对于 $x$ , 那么对于 $y\in P, y\ne x$ $c^T y \leq 0$ 接下来证明唯一性，假设 $c^Ty=0$ 那么对于所有 $j \notin B$ 有 $y_j=0$ 然后 $b=A y=A_B y_B=A x=A_B x_B$ 然后变形$A_B\left(x_B-y_B\right)=0$ 以为 $A_B$ 有 independent column 所以 $x_B -y_B = 0$ 所以 $x_B=y_B$ 所以 $x=y$

Observation

对于一个 LP 我们可以不妨假设 $\operatorname{rank}(A)=m$ , 也就是满秩

解释

假设 $\operatorname{rank}(A)<m$ 那么可以不妨假设 $A_1=\sum_{i=2}^m \lambda_i \cdot A_i$ 也就是 $A_1$ 可以表示为其他行的线性组合

$b_1=\sum_{i=2}^m \lambda_i \cdot b_i$ 那么 $A_1$ 就没用了，就把第一行去掉
$b_1 \neq \sum_{i=2}^m \lambda_i \cdot b_i$ 这种情况LP是infeasible的

定理 24 Basis

给定 LP $P=\{x \mid A x=b, x \geq 0\}$ 且 $x$ 是 extreme point 等价于存在 $B \subseteq\{1, \ldots, n\}$ with $|B|=m$ 我们叫 $B$ 是一个 Basis

$A_B$ is non-singular
$x_B=A_B^{-1} b \geq 0$
$x_N=0$

其中 $N=\{1, \ldots, n\} \backslash B$

对于任意矩阵, 行秩等于列秩

证明

($\Leftarrow$)

有 $A_B$ non-singular 就是有 linearly independent columns, 那么把 $x_j=0$ 的列踢掉，也是independent的, 所以是extreme point.

($\Rightarrow$)

首先extreme point 可以推出设 $B=\left\{j \mid x_j>0\right\}$ 那么 $x$ 是 extreme point iff $A_B$ 有 linearly independent columns. 首先因为行秩是 $m$ , 列秩也是 $m$. 所以如果 $|B|< m$ , 加一些可以加列进去之后仍然是 linearly independent 把 $m$ 列补齐，构造出满足条件 1 的 $B$ . 所以 $A_Bx_B=b$ 推出 $x_B=A_B^{-1} b \geq 0$ 然后条件3显然满足.

定义 Basic Feasible Solutions

$\mathcal{x} \in \mathbb{R}^n$ 是 basic solution 若 $Ax=b$ 且 $\operatorname{rank}\left(A_J\right)=|J|$ where $J=\left\{j \mid x_j \neq 0\right\}$

$x$ 是 basic feasible solution (BFS) 若还 $x\ge 0$

$x$ 是 basic solution associated to basis $B$, 若 $A_B x_B=b$ and $x_j=0$ 对于所有 $j \notin B$

定义 25 basic feasible solution

对于 general LP $\max \left\{c^T x \mid A x \leq b\right\}$ 若 $x$ 是BFS 若 $x$ 是 feasible 且存在 $n$ 个linearly independent constraints is tight. (以等于号满足)

解释

一个BFS 满足 $m$ 个equality constraint 就是 $A$ 的所有行, 此外至少 $n-m$ 个 $x_i$ 是$0$ 满足 $x $ 是以等于号成立.

所以至少 $n$ 个 constraint 是以等于号满足的

然后可以回答之前的问题: Is LP in NP?

对于 LP 我们可以便利所有 bases 然后计算，如果 LP 是unbounded 我们可以把 $c^T x \le \alpha$ 加入constraint, 这样一定是bounded了.

Simplex Algorithm

BFS 移动到相邻的 BFS 来计算最优解.

选择一个 coefficient 大于零的作为进入的variable
增大 $b$ 并且使得constraint 满足
$\theta=\min \{480 / 15,160 / 4,1190 / 20\}$ 选自最小的步长
变成 $0$ 的出来.

知道没有可以换的时候结束

\[ \begin{array}{rlrl}\max 13 a+23 b & & \\ \text { s.t. } \quad 5 a+15 b+s_c & =480 \\ 4 a+4 b+s_h & =160 \\ 35 a+20 b+s_m & =1190 \\ a, b, s_c, s_h, s_m & \geq 0\end{array} \]

最后是

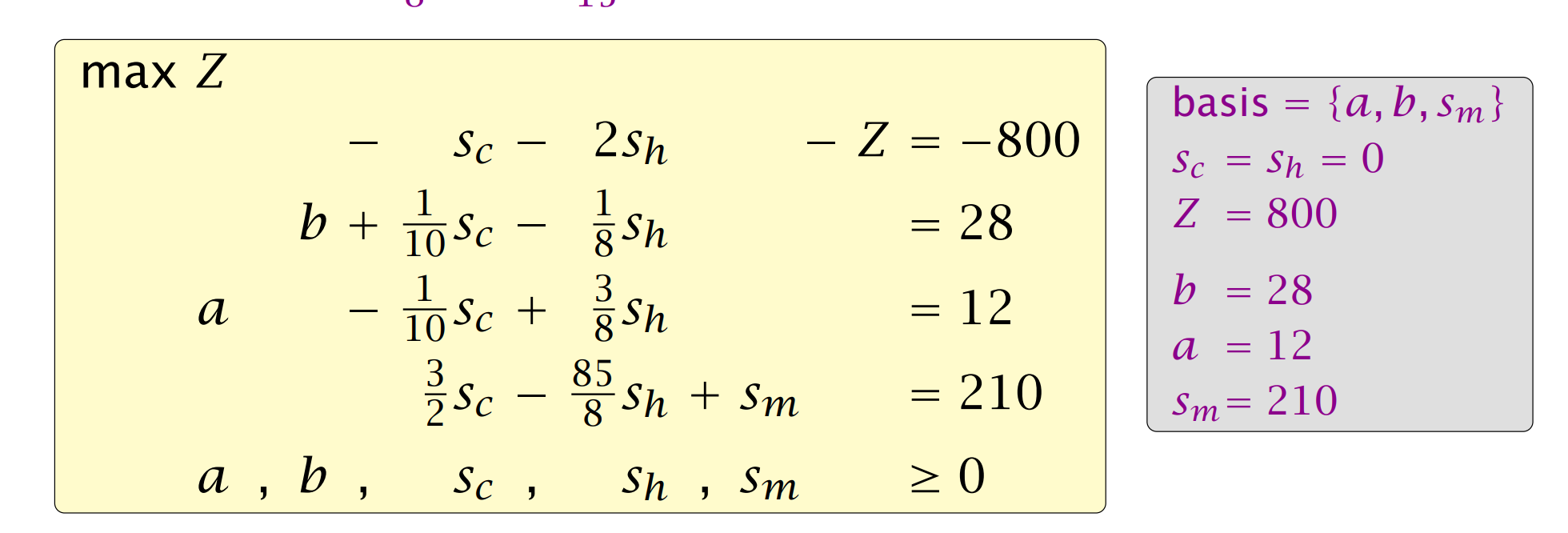
这样子 $Z=800-s_C-2 s_h, s_C \geq 0, s_h \geq 0$

矩阵表示法

\[ \begin{array}{rlrl} c_B^T x_B+c_N^T x_N & =Z \\ A_B x_B+A_N x_N & =b \\ x_B, x_N \geq 0 \end{array} \]

simplex tableaux是

\[ \begin{aligned} I\left(c_N^T-c_B^T A_B^{-1} A_N\right) x_N & =Z-c_B^T A_B^{-1} b \\ I x_B+A_B^{-1} A_N x_N & =A_B^{-1} b \\ x_B, & \geq 0 \end{aligned} \]

就是看这是怎么用矩阵算出来的

Algebraic Definition of Pivoting

给定Basis $B$ with BFS $x^*$ 选择 $j \notin B$ 使得 increase $x_j^*$ from 0 to $\theta>0$

Go from $x^*$ to $x^*+\theta \cdot d$

然后需要满足

$d_j=1$ normalization
$d_{\ell}=0, \ell \notin B, \ell \neq j$
$A\left(x^*+\theta d\right)=b$ must hold. Hence $A d=0$.
$A_B d_B+A_{* j}=A d=0$ 所以 $d_B=-A_B^{-1} A_{* j}$

定义 26 j-th basic direction

其中的 $d_B=-A_B^{-1} A_{* j}$ 是 j-th basic direction, 然后从 $x^*$ 走到 $x^*+\theta \cdot d$ , 目标函数会增加

\[ \theta \cdot c^T d=\theta\left(c_j-c_B^T A_B^{-1} A_{* j}\right) \]

定义 27 Reduced Cost

对于 $B$

\[ \tilde{c}_j=c_j-c_B^T A_B^{-1} A_{* j} \]

是对于 $x_j$ 的reduced cost, 其实是增加的cost

其实是 $c_N^T-c_B^T A_B^{-1} A_N$ 的第 $j$ 项

Min Ratio Test

如果所有 $\theta$ 是负的，那么是unbounded

定义 28 Degeneracy

如果 $x_l=0, l\in B$ 那么目标函数可能不会增大. 多点重合的情况.

BFS $x^*$ 是 degenerate 若 $J=\left\{j \mid x_j^*>0\right\}$ 是 $|J| < m$

所以这种情况，算法可能会无限循环.

Two Phase Algorithm得出初始可行解

如果 $A x \leq b, x \geq 0$, and $\boldsymbol{b} \geq \mathbf{0}$. 那么我们可以令 $x=0$

令slack variable 等于右边

如果没有的话就要用 TWO PHASE ALGORITHM

令 $b_i<0$ 的行乘 $-1$
maximize $-\sum_i v_i$ 使得 $A x+I v=b, x \geq 0, v \geq 0$ using Simplex

我们要尽可能不使用 $v$, 也就是令 $v=0$
如果 $\sum_i v_i>0$ 那么就是infeasible

否则你就有一个初始的可行解

Lemma 29 最优解判定条件

Let $B$ be a basis and $x^*$ a BFS corresponding to basis $B . \tilde{c} \leq 0$ implies that $x^*$ is an optimum solution to the LP.

怎样得到解的上界

\[ \begin{aligned} \max 13 a+23 b & \\ \text { s.t. } 5 a+15 b &\leq 480 \\ 4 a+4 b &\leq 160 \\ 35 a+20 b &\leq 1190 \\ a, b &\geq 0 \\ \end{aligned} \]

可以构造一个不等式的 conic combination 比如1行乘以2再加2行

Duality

定义 30 Dual problem

对于LP $z=\max \left\{c^T x \mid A x \leq b, x \geq 0\right\}$ 的dual problem就是构造最小的上界

\[ w=\min \left\{b^T y \mid A^T y \geq c, y \geq 0\right\} \]

Lemma 31

The dual problem of the dual problem is the primal problem

证明

$w=\min \left\{b^T y \mid A^T y \geq c, y \geq 0\right\}$ 对于这个再dual一次，都乘个符号变成max

$w=-\max \left\{-b^T y \mid-A^T y \leq-c, y \geq 0\right\}$ 然后再dual 就变成 $z=-\min \left\{-c^T x \mid-A x \geq-b, x \geq 0\right\}$ 再转成min就是 $z=\max \left\{c^T x \mid A x \leq b, x \geq 0\right\}$

Weak duality

Let $\hat{x}$ be primal feasible 就是再primal problem 里面是feasible的, $\hat{y}$ be dual feasible. Then

\[ c^T \hat{x} \leq z \leq w \leq b^T \hat{y} \]

证明

$A^T \hat{y} \geq c \Rightarrow \hat{x}^T A^T \hat{y} \geq \hat{x}^T c (\hat{x}\ge 0)$ 左右乘个 $\hat{x}^T$ $A \hat{x} \leq b \Rightarrow y^T A \hat{x} \leq \hat{y}^T b(\hat{y} \geq 0)$ , 然后呢因为scalar来说转置不改变结果，所以

\[ c^T \hat{x} \leq \hat{y}^T A \hat{x} \leq b^T \hat{y} \]

因为他们是feasible的，所以存在 $c^T \hat{x}=z$ 使得他们两个分别可以达到最优解所以 $z \leq w$

Simplex 的dual form

\[ \begin{aligned} z & =\max \left\{c^T x \mid A x=b, x \geq 0\right\} \\ w & =\min \left\{b^T y \mid A^T y \geq c\right\} \end{aligned} \]

证明

\[ \begin{aligned} \max & \left\{c^T x \mid A x=b, x \geq 0\right\} \\ & =\max \left\{c^T x \mid A x \leq b,-A x \leq-b, x \geq 0\right\} \\ & =\max \left\{c^T x \mid\left[\begin{array}{c} A \\ -A \end{array}\right] x \leq\left[\begin{array}{c} b \\ -b \end{array}\right], x \geq 0\right\} \end{aligned} \]

把等于号拆成2个小于等于，然后写成矩阵，然后求dual

\[ \begin{aligned} \min & \left\{\left[b^T-b^T\right] y \mid\left[A^T-A^T\right] y \geq c, y \geq 0\right\} \\ & =\min \left\{\left[b^T-b^T\right] \cdot\left[\begin{array}{c} y^{+} \\ y^{-} \end{array}\right] \mid\left[A^T-A^T\right] \cdot\left[\begin{array}{c} y^{+} \\ y^{-} \end{array}\right] \geq c, y^{-} \geq 0, y^{+} \geq 0\right\} \\ & =\min \left\{b^T \cdot\left(y^{+}-y^{-}\right) \mid A^T \cdot\left(y^{+}-y^{-}\right) \geq c, y^{-} \geq 0, y^{+} \geq 0\right\} \\ & =\min \left\{b^T y^{\prime} \mid A^T y^{\prime} \geq c\right\} \end{aligned} \]

Proof of Optimality Criterion for Simplex

首先由 reduced cost $\tilde{c}=c^T-c_B^T A_B^{-1} A \leq 0$ 然后求个转置

\[ A^T\left(A_B^{-1}\right)^T c_B \geq c \]

所以 $\mathcal{Y}^*=\left(A_B^{-1}\right)^T c_B$ 是一个是dual problem的解，然后代入dual定义

\[ \begin{aligned} b^T y^* & =\left(A x^*\right)^T y^*=\left(A_B x_B^*\right)^T y^* \\ & =\left(A_B x_B^*\right)^T\left(A_B^{-1}\right)^T c_B=\left(x_B^*\right)^T A_B^T\left(A_B^{-1}\right)^T c_B \\ & =c^T x^* \end{aligned} \]

$x^*$ 是你当前求出来的最优解

Strong Duality

首先如果我们有min的LP，我们也可以写Dual 也就是 \[ D=\min \left\{\bar{b}^T y \mid \bar{A}^T y=c, y \geq 0\right\} \] 和下面这个是一组 \[ \bar{P}=\max \left\{c^T x \mid \bar{A} x \leq \bar{b}\right\} \]

高效算法II

线性规划(LP)

Standard Form

转换成Standard Form

定义1 线性规划(LP)

一些基本定义

定义2 linear combination

定义3 Linear space

定义4 span

定义 5 convex function

Lemma 6 convex P

定义 7 affine subspace

定义 8 convex set

定义 9 hyperplane

定义 10 halfspace

定义 11 polytop

定义 12 Polyhedron

定义 13 Bounded Polyhedron

定理 14 polytop and polyhedron

定义 15 supporting hyperplane

定义 16 Face

定义 17 edge and facet

定义 18 等价定义 vertex

定义 19 extreme point

Lemma 20 vertex and extreme point

Observation

Convex Set

定理 21 答案在端点

记号 Submatrix

定理 22 extreme point

定理 23 vertex

Observation

定理 24 Basis

定义 Basic Feasible Solutions

定义 25 basic feasible solution

Simplex Algorithm

矩阵表示法

Algebraic Definition of Pivoting

定义 26 j-th basic direction

定义 27 Reduced Cost

Min Ratio Test

定义 28 Degeneracy

Two Phase Algorithm得出初始可行解

Lemma 29 最优解判定条件

怎样得到解的上界

Duality

定义 30 Dual problem

Lemma 31

Weak duality

Simplex 的dual form

Proof of Optimality Criterion for Simplex

Strong Duality