网络流思路汇总
网络流理论
网络
定义1.1 一个网络 \(N=(V,A)\) 是指一个连通无环弧且满足下列条件的有向图:
- 由一个顶点子集 \(X\),其每个顶点的入读都为0
- 由一个与 \(X\) 不相交的顶点子集 \(Y\) ,其每个顶点出度都为0
- 每条弧都有一个非负的权值,成为弧的容量
上述网络可以写成 \(N=(V,X,Y,A,C)\) ,\(X\) 是源点集,\(Y\)是汇点集合,其他顶点成为中转点,\(C\) 是网络的容量函数。它是定义在弧 \(A\) 上的非负函数
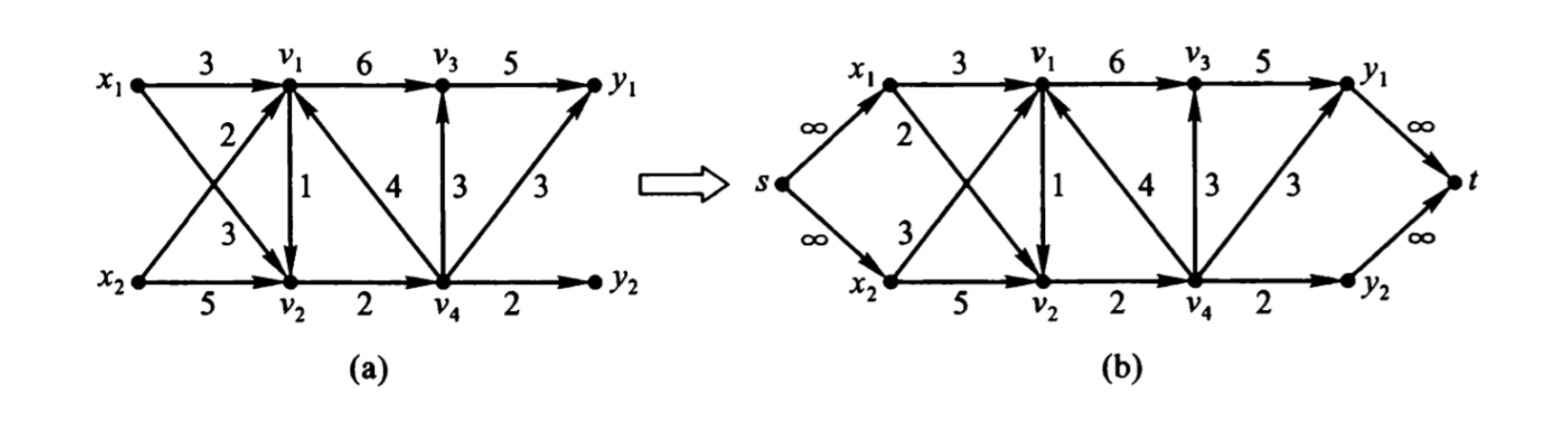
如果源点集和汇点集都只含一个顶点,那么这个网络是单源单汇网络 。任何一个网络可以转换成一个单源单汇的网络,方法是加一个超级源点和超级汇点
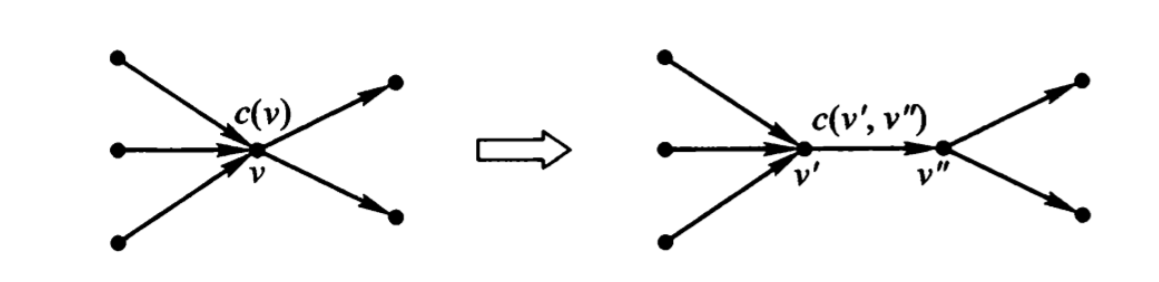
如果顶点需有容量,那么可以用拆点的方法实现:
网络流与割
定义1.2 网络 \(N=(V,X,Y,A,C)\) 中的一个(可行)流是指定义在 \(A\) 上的一个整值函数\(f\) ,使得
- 对 \(\forall a \in A, 0 \leqslant f(a) \leqslant c(a)\), 容量约束
- 对\(\forall v \in V-(X \cup Y), f^{-}(v)=f^{+}(v)\) ,流量守恒
其中 \(f^{-}(v)\) 表示入弧的流量之和,$ f^{+}(v)$ 表示 \(v\) 出弧的流量之和 \[ f^{+}(v)=\sum_{u \in V} f(v, u),f^{-}(v) =\sum_{u \in V} f(u, v) \] 可行流总是存在的,比如 \(\forall a \in A, f(a)=0\) . 2. \(f^{-}(S)\) 表示流入\(S\)的流量,\(f^{+}(v)\) 表示流出\(S\) 的流量
定义1.3 设 \(f\) 是网络 \(N=(V,X,Y,A,C)\) 的一个可行流,则必有 $ f^{+}(X)= f^{-}(Y)$ 。\(f^{+}(X)\) 称为\(f\) 的流量。记 $f $ 。 $ N$ 中流量最大的可行流为 \(N\) 的最大流
定义1.4 设 \(N=(V,x,y,A,C)\) 是一个单源单汇网络,\(S \subseteq V, \overline{S}=V-S\) . 用 \((S,\overline{S})\) 表示从\(S\) 指向 \(S\) 以外的所有弧的集合。若 \(x \in S,y \in \overline{S}\) 那么\((S,\overline{S})\) 就是网络 \(N\) 的一个割。一个割\((S,\overline{S})\) 的容量指其中各条弧的容量之和,记为\(\text{Cap}(S,\overline{S})\) 。
一个网络\(N\) 可能有多个割,其中容量最小的割成为最小割
定义1.5 一个网络的割\(K\) 是最小割,如果网络\(N\) 中不存在割\(K'\) ,使得\(\text{Cap}K' < \text{Cap}K\)
引理1.1 对网络中任意流 \(f\) 和割 \((S,\overline{S})\) 均有 \(\text{Val}f=f^{+}(S) - f^{-}(\overline{S})\)
证明: 设\(f\) 是网络 \(N=(V,x,y,A,C)\) 中的流,\((S,\overline{S})\) 是 \(N\) 的一个割,由流的定义: \[ f^{+}(x)=\operatorname{Val} f, f^{-}(x)=0, f^{+}(v)-f^{-}(v)=0,(\forall v \in S-\{x\}) \] 所以 \[ \begin{aligned} Val f &=f^{+}(x)-f^{-}(x)+\sum_{v \in S-\{x\}}\left[f^{+}(v)-f^{-}(v)\right]=\sum_{v \in S}\left[f^{+}(v)-f^{-}(v)\right] \\ &=\sum_{v \in S}\left[\sum_{u \in V} f(v, u)-\sum_{u \in V} f(u, v)\right]=\sum_{v \in S} \sum_{u \in V} f(v, u)-\sum_{v \in S} \sum_{u \in V} f(u, v) \\ &=\sum_{v \in S} \sum_{u \in S} f(v, u)+\sum_{v \in S} \sum_{u \notin S} f(v, u)-\sum_{v \in S} \sum_{u \in S} f(u, v)-\sum_{v \in S} \sum_{u \notin S} f(u, v)\\ &=\sum_{v \in S} \sum_{u \notin S} f(v, u)-\sum_{v \in S} \sum_{u \notin S} f(u, v) \\&=f^{+}(S)-f^{-}(S) \end{aligned} \] 第二行用了分配律展开,第三行是把在 \(V\) 中的点拆成了在 \(S\) 中的和不在\(S\) 中的点 。第三行的第一项和第三像是一个集合中正向边和反向边的关系,所以相等抵消。最后一行的意思就是从\(S\) 中出发到\(\overline{S}\)的弧流量之和。证毕。
定义1.6 设 \(N=(V,x,y,A,C)\) 是一个网络,\(f\) 是\(N\) 的一个可行流,对\(N\) 中任意一条弧\(a\) :
- 若\(f(a)=0\) ,那么\(a\) 是\(f\) 零的
- 若\(f(a)>0\) ,那么\(a\) 是\(f\) 正的
- 若\(f(a)=c(a)\) ,那么\(a\) 是\(f\) 饱和的
- 若\(f(a)<c(a)\) ,那么\(a\) 是\(f\) 非饱和的
定理1.1 对网络\(N\) 中的任一可行流\(f\) 和任一割\(K=(S,\overline{S})\), 均有\(\text{Val}f \leqslant \text{Cap}K\) 。其中等式成立当且仅当\((S,\overline{S})\)中的每条弧都是饱和的而\((\overline{S},S)\)中每条弧都是\(f\)零的
证明:因为\(f\) 是可行流,所以: \[ f^{+}(S)=\sum_{a \in K} f(a) \leqslant \sum_{a \in K} c(a)=\operatorname{Cap} K ,\text{并且}f^{-}(S)=\sum_{a \in(\bar{S}, S)} f(a) \geqslant 0 \] 由引理1.1知:\(\text{Val}f=f^{+}(S)-f^{-}(S) \leqslant \operatorname{Cap} K\) ,所以第一个结论成立。而当\((S,\overline{S})\)中的每条弧都是饱和的而\((\overline{S},S)\)中每条弧都是\(f\)零的,显然 \(\text{Val}f=f^{+}(S)-f^{-}(S)=f^{+}(S)=\operatorname{Cap} K\),反之若 \(\text{Val}f=\operatorname{Cap}K\),则 \(\operatorname{Cap} K=\operatorname{Val} f=f^{+}(S)-f^{-}(S) \leqslant \operatorname{Cap} K-f^{-}(S)\) ,由于\(f^{-}(S) \geqslant 0\),则必定\(f^{-}(S)=0\) 且\(f^{+}(S)=\operatorname{Cap} K\) 证毕
推论1.1 设\(f\) 是网络 \(N\) 的一个可行流,\(K\) 是\(N\) 的一个割,若\(\text{Val}f=\text{Cap}K\) ,则\(f\) 是最大流而\(K\) 是最小割
证明:设网络中的最大流 \(f^{\star}\) ,最小割为 \(K^{\star}\),由定理知道\(\text{Val}f^{\star}\leqslant\text{Cap}K^{\star}\) ,从而 \(\text{Val}f \leqslant \operatorname{Val} f^{\star} \leqslant \operatorname{Cap} K^{\star} \leqslant \operatorname{Cap} K\) . 由已知条件\(\text{Val}f=\text{Cap}K\) 得出\(\text{Val}f=\text{Val}f^{\star}\) ,\(\operatorname{Cap} K = \operatorname{Cap} K^{\star}\)
定义1.7 设\(u,v\) 是网络 \(N=(V,x,y,A,C)\) 中的任意两点。\(P\) 是\(N\) 的底图中一条连接\(u\)与\(v\) 的无向路,若规定路\(P\) 从\(u\) 到 \(v\) ,则这样规定了走向的路\(P\) 为网络中的一条\(u\) 到\(v\) 的路,简称\(u\text{-}v\)路。一条从源点\(x\) 到汇点\(y\) 的路叫\(x\text{-}y\) 路
定义1.8 设 \(P=u v_{1} \cdots v_{k} v\) 是网络 \(N=(V,x,y,A,C)\) 中的一条\(u\text{-}v\) 路,若弧\(\left\langle v_{i}, v_{i+1}\right\rangle \in A\) 那么此弧是 \(u\text{-}v\)路上的正向弧,若弧\(\left\langle v_{i+1}, v_{i}\right\rangle \in A\) 那么它是反向弧。
定义1.9 设\(f\) 是网络 \(N=(V,x,y,A,C)\) 中的一个可行流,\(u\) 是\(N\) 中的任意一点,\(P\) 是\(N\) 中一条\(x\text{-}u\)路,如果路\(P\) 上的一条弧\(a\),都有
- 若弧\(a\) 是\(P\) 的正向弧,则\(c(a)-f(a)>0\)
- 若弧\(a\) 是\(P\) 的反向弧,则\(f(a)>0\)
则称\(P\) 是\(N\) 中的一条可增\(x\text{-}u\) 路。特别地,\(N\) 中的一条\(f\) 可增\(x\text{-}y\)路简称为\(N\) 的一条\(f\) 可增路
对\(N\) 中任意一条\(f\) 可增路\(P\) 和\(P\) 上的任意一条弧\(a\), 令 \[ \Delta f(a)=\left\{\begin{array}{l} c(a)-f(a), 若a是正向弧\\ f(a),若a是反向弧 \end{array}\right. \] 则沿\(P\) 路可增加的流量为\(\Delta f(P)=\min _{a \in P} \Delta f(a)\) ,则称该值为\(f\) 可增路\(P\) 上流的增量或可增量
定理1.2 最大流最小割定理
任一个网络 \(N=(V,x,y,A,C)\) 中,最大流的流量等于最小割的容量
证明:设网络中的最大流\(f^{*}\) ,最小割为\(K^{*}\),由定理1.1\(\text{Val}f^{*}\leqslant\text{Cap}K^{*}\),
另一方面,令 \[ S=\{u \in V | N 中有f^{*} 可增x\text{-}u路\} \cup\{x\} \] 则 \(y \notin S\) ,否则可以增广得到更大的流。而源\(x \in S\),从而\(K=(S,\overline{S})\) 是\(N\) 中的一个割。对于\((S,\overline{S})\) 中的任意一条弧\(a=\langle u, v\rangle\) ,必定\(f^{*}(a)=c(a)\),否则\(P+a\) 是条可增广的\(x\text{-}v\)路,\(v\)应该在\(S\) 中。同理,对于\((\overline{S},S)\) ,必定\(f^{*}(a)=0\) .也就是说\((S,\overline{S})\)的弧都是饱和的,而\((\overline{S},S)\)的弧都是零的。所以由定理1.1 知:\(\text{Val} f^{*}=\operatorname{Cap}(S, \bar{S}) \geqslant \operatorname{Cap} K^{*}\)
所以\(\text{Val} f^{*}= \text{Cap}K^{*}\),证毕
最大流问题及其标号算法
最大流问题:给定网络 \(N=(V,x,y,A,C)\) ,如何求\(N\) 中的最大流?
由可增路的概念,对网络\(N\) 中一个可行流\(f\) ,如果能找到\(N\) 中的一条\(f\) 可增\(x\text{-}y\) 路\(P\) ,则可以沿着\(P\) 修改流,得到更大的可行流\(\hat{f}\) ,修改办法如下: \[ \widehat{f}(a)=\left\{\begin{array}{l} f(a)+\Delta f(P),若a是P的正向弧 \\ f(a)-\Delta f(P) ,若a是P的反向弧\\ f(a),a不在P上 \end{array}\right. \] 修改后的流量为:\(\operatorname{Val} \widehat{f}=\operatorname{Val} f+\Delta f(P)\)
所以我们可以反复找\(N\) 中的可增路,沿着可增路增大,直到找不到可增路为止。
定理2.1 网络 \(N=(V,x,y,A,C)\) 中的可行流\(f\) 是\(N\) 的最大流当且仅当\(N\) 中不存在\(f\) 可增路
证明: 必要性:若\(N\) 有可增路,则\(f\) 不是最大流,因为可以沿\(P\) 增广得到更大的流
充分性:设\(N\) 中不存在\(f\) 的可增路,令\(S=\{u \in V | N 中有f^{*} 可增x\text{-}u路\} \cup\{x\}\),和证明最大流最小割定理类似,我们可以证明\(K=(S,\overline{S})\) 是一个割,且\(\text{Val} f= \text{Cap}K\)。再由推论1.1知道\(f\) 是最大流。
Dinic算法
增量网络
增量网络就是对于每一条存在的流, 减去已经使用过的流,再加入反向边(使得可以"反悔"的边)形成的网络.
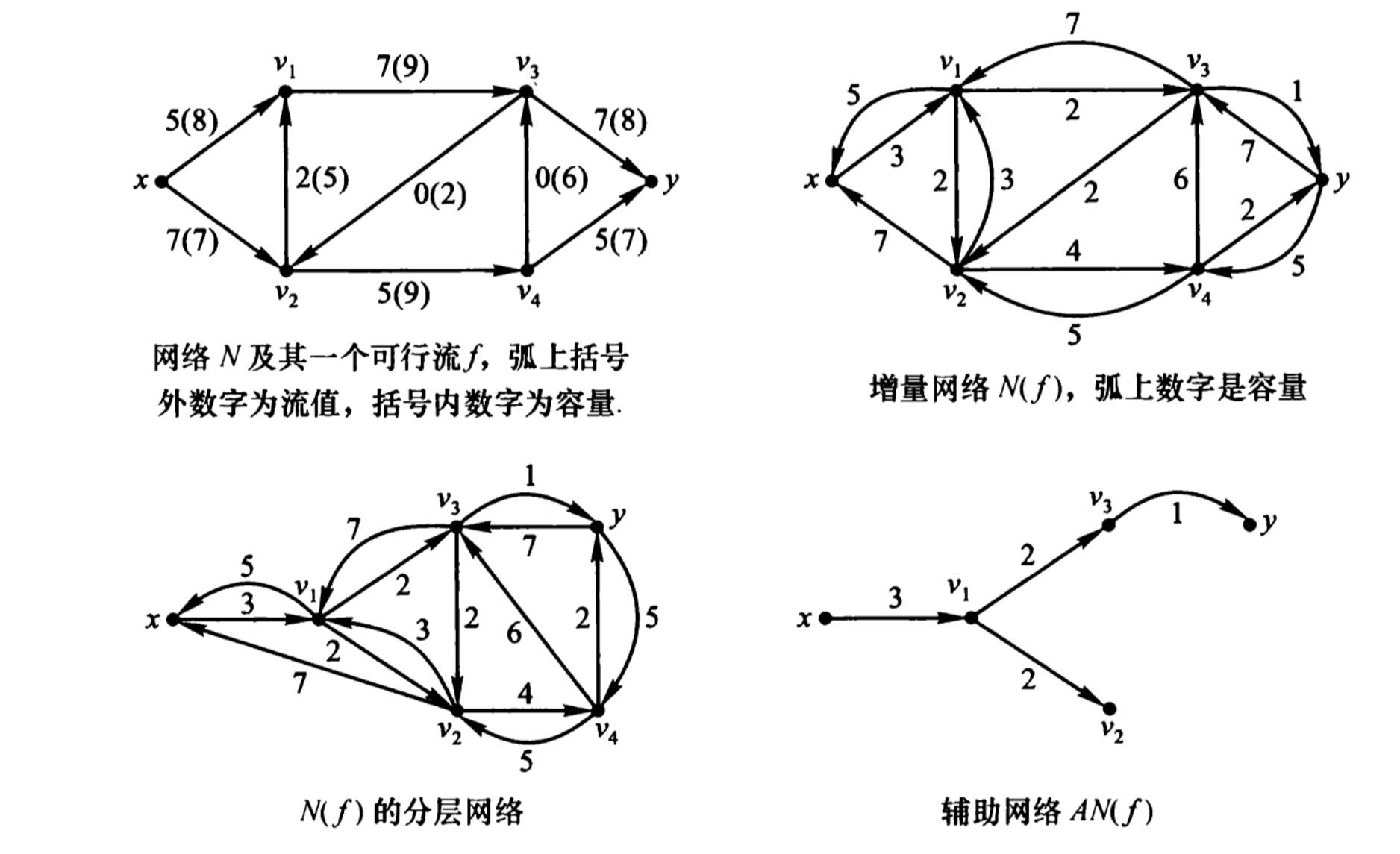
定义3.1 对于网络 \(N=(V,x,y,A,C)\) 和\(N\) 上的一个可行流\(f\) ,构造一个新网络 \(N(f)=(V,x,y,A(f),C')\),其中\(A(f)\) 和\(C'\) 的定义如下
- 若 \(\langle u, v\rangle \in A\) 且 \(f(u, v)<c(u, v)\),则\(\langle u, v\rangle \in A(f)\), 且 \(c^{\prime}(u, v)=c(u, v)-f(u, v)\)
- 若 \(\langle u, v\rangle \in A\) 且 \(f(u, v)>0\),则\(\langle v, u\rangle \in A(f)\), 且\(c^{\prime}(v, u)=f(u, v)\)
这样构造的网络\(N(f)\) 称为网络\(N\) 关于流\(f\) 的增量网络
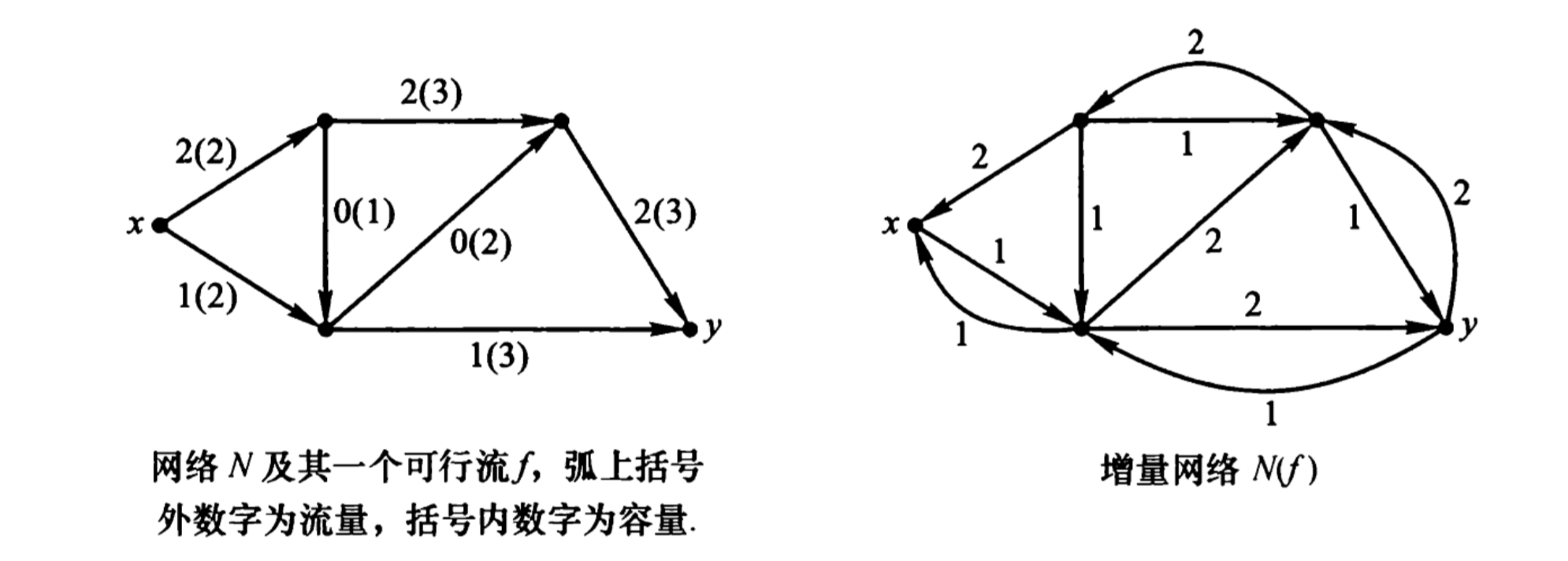
其实上面的操作相当于是加入了反向边的”反悔“操作。我们可以知道\(N(f)\)中的每条弧的容量恰为\(N\) 中相应弧的流可增量。严格来说,增量网络严格意义上不符合网络的定义,因为没有入度为0和出度为0的源和汇。但由于它是基于网络定义的,我们仍然将其看作网络,其中\(x\) 和\(y\) 分别为源和汇,该网络的一个可行流\(f\) 定义为 \[ \left\{\begin{array}{l} f(x)=f^{+}(x)-f^{-}(x) \geqslant 0 \\ f(y)=f^{+}(y)-f^{-}(y) \leqslant 0 \\ f(u)=f^{+}(u)-f^{-}(u)=0 \end{array}\right. \] 我们将\(N(f)\) 中从\(x\) 到 \(y\) 的有向路成为增量网络\(N(f)\) 的\(x\text{-}y\) 有向路。显然一个有向路就对于了原来网络的可增路,两者是等价的。
定理3.2 设\(f^{*}\) 是网络\(N\) 中的最大流,\(f\) 是\(N\) 中的一个可行流,则增量网络\(N(f)\) 中的最大流的流量为\(\text{Val}f^{*}-\text{Val}f\) .
证明:
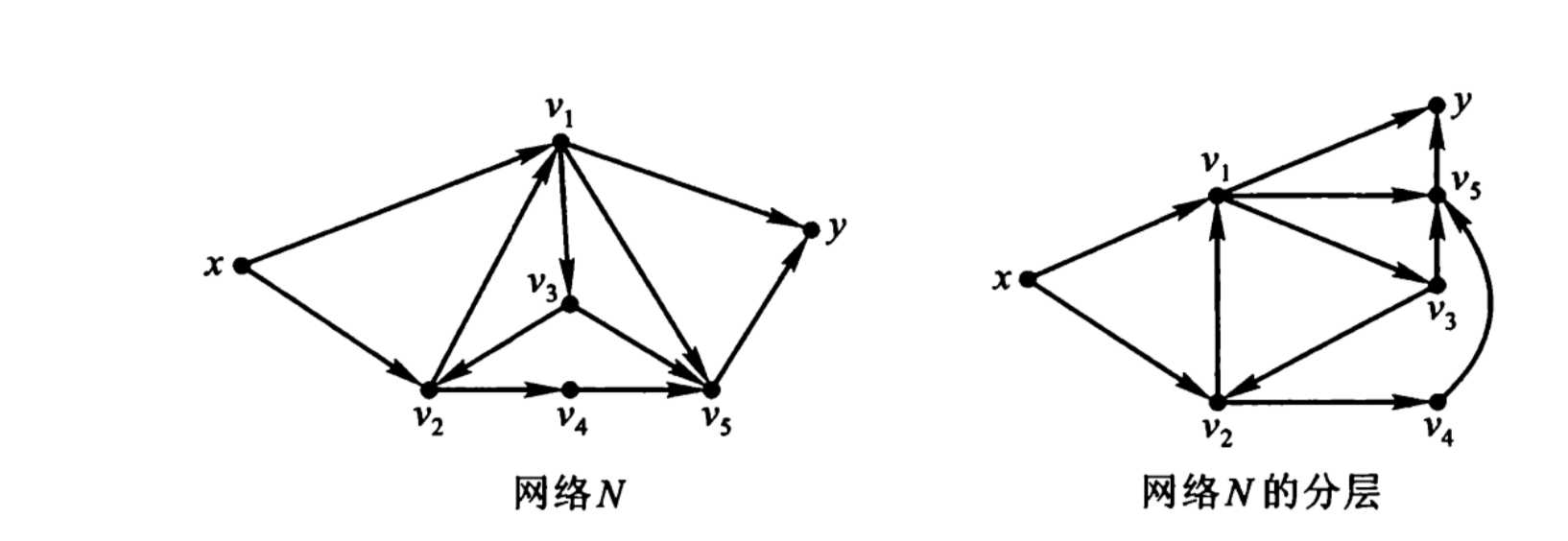
网络顶点分层
设网络 \(N=(V,x,y,A,C)\) ,令$
V_{i}={v V | N 中x到v的最短有向路的长为i}\(.设\)x$ 到\(y\) 的最短有向路的长为\(n\) ,则\((1) x
\in V_{0}, y \in V_{n} ;(2) V_{i} \cap V_{j}=\varnothing,(j \neq
i)\). \(V_{i}\)
中的节点称为网络\(N\) 的第\(i\) 层顶点。 \[
V_{0}=\{x\}, V_{1}=\left\{v_{1}, v_{2}\right\}, V_{2}=\left\{v_{3},
v_{4}, v_{5}, y\right\}
\] 
辅助网络
定义3.2 设\(f\) 是网络\(N=(V,x,y,A,C)\) 的一个可行流,\(N(f)\) 是\(N\) 关于流 \(f\) 的增量网络。对\(N(f)\) 的顶点按最短有向路分层后,删去比\(y\) 层数高的顶点及与\(y\) 同层的顶点(保留\(y\)),再删去从高层指向低层的弧及同层顶点间的弧,所剩的各条弧上的容量与\(N(f)\) 中相同。这样得到的网络是\(N(f)\) 的子网络,称为\(N\) 关于\(f\) 的辅助网络,记为\(AN(f)\).
最小费用流问题
定义6.1 对于网络\(N=(V,x,y,A,C)\), 给其每条弧 \(\langle u, v\rangle\) 赋以一个非负实数 \(w(u,v)\),称为弧 \(\langle u, v\rangle\) 的费用。这种每条弧都带有费用的网络,称为费用网络,记为 \(N=(V,x,y,A,C,w)\), 或 \(N=(V,A,C,w)\) ,其中\(w\) 为费用函数。费用网络\(N=(V,x,y,A,C,w)\)中流\(f\) 的费用定义为 \[ w(f)=\sum_{\langle u, v\rangle \in A}[w(u, v) \cdot f(u, v)] \] 最小费用流问题:对于网络\(N=(V,x,y,A,C,w)\) 和一个给定的数\(v_{0} \geqslant 0\) ,求\(N\) 中流量为\(v_{0}\) 且费用最小的可行流。
Push-Relabel
这个算法的思想是,把流量看做是水流。每个节点都有个高度,水从高处往低处流。
Preflow
对于一个给定的网络 \(G =(V, E)\) , 容量函数是 \(c\) , 一个Preflowd定义为 \[ \forall (u,v) \in E: 0 \leq f(e) \leq c(e) \\ \forall u \in V \ \{s,t\}: \sum_{\{v:(v,u)\in E\}} f(v,u)-\sum_{\{v:(u,v)\in E\}}f(u,v) \ge0 \] 也就是说: ”在这个网络里面,允许某个入流大于出流的流“
Excess flow
对于一个网络 \(G\) 和一个 preflow \(f\) ,某个节点的 excess flow 定义为 \[ e(u) = \sum_{\{v:(v,u)\in E\}} f(v,u)-\sum_{\{v:(u,v)\in E\}}f(u,v) \] 一个节点 \(u \in V \ \{s,t\}\) 是 overflowing 若 \(e(u) > 0\)
也就是入流减去出流的值
Height高度
对于一个网络 \(G\) 和一个流 \(f\) ,一个函数 \(h: V \rightarrow N\) 是一个高度函数, 若 \(h(s) = |V|\), \(h(t) = 0\) 且 \(h(u) \le h(v) + 1\) 对于每个在残量网络上的边 \((u,v) \in E_f\) 成立
我们有push和relabel两个操作
Push操作
若 \(u\) 是 overflowing 的,把当前节点的流量推送到周围高度正好比他低\(1\)的节点,这些节点必须满足 \(h_v = h_u +1\)
Relabel操作
若 \(u\) 是 overflowing 的, 且对于所有的邻居 \(h(u) \le h(v)\) , 那么把 \(h(u)\) 设置为 \(1+ min\{h(v):(u,v)\in E_f\}\) ,也就是邻居的最小高度 \(+1\)
Push-Relabel算法, 初始版本
1 | for each vertex v do |
证明
性质
- \(x\) 是一个 preflow
- \(h(s)=|V|\) ,\(h(t) = 0\)
- 若 \((v,w) \in E\) 在残量网络里的,那么 \(h(v) \le h(w)+1\)
定理 5.1
初始化之后,以上三种性质全部满足
定理 5.2
若 \(v \in V\) 是一个激活的点,那么在残量网络里面存在一条从 \(v\) 到源头的有向路径
定理 5.2
push操作过后,以上三条性质依然成立
定理 5.3
relabel操作保持上述三条性质,并且 \(v\) 的高度至少增加 \(1\)
网络流模板
一些代码模板的约定
1 | typedef int typec; // 方便换类型 |
Dinic算法
算法的总体顺序是:先建立层次图,然后每次增广,每次增广都把流量加上
1 | typec dinic() { |
建立层次图的时候,从源点s开始,源点的深度设为1,根据bfs的顺序递增
1 | bool bfs() { |
dfs深搜进行增广,还是从s开始增广,flow是当前可以增广的流量,开始时正无穷。
1 | typec dfs(int x, typec flow) { |
完整模板:
1 |
|
最小费用流算法
1 |
|
网络流思路
最大流思路
最小割思路
- 最小割的思路可以假设收益最大化,然后损失最小的价值。这个最小损失价值就可以用最小割模拟
- 满足所要求必须割断边,使得源点和汇点不连通
例题CF311E Biologist
假设我们已经满足了所有的要求,那么最大的收益是每个要求满足后的收益的和那么问题就等价于,我损失哪些要求,可以让我得到最小的损失。在建图的时候用最小割的思维考虑,使得最后的最小割就是最小的损失。 \[ ans=\sum_{i=1}^{m} w_{i} -MinCut \] 所以边就一定要和价值联系到一起。我们考虑一个要求:
- 要么我割断所有改变0和1的边来满足它
- 要么我放弃这个要求,割断它的价值边
那么我们的建图就可以这么考虑:
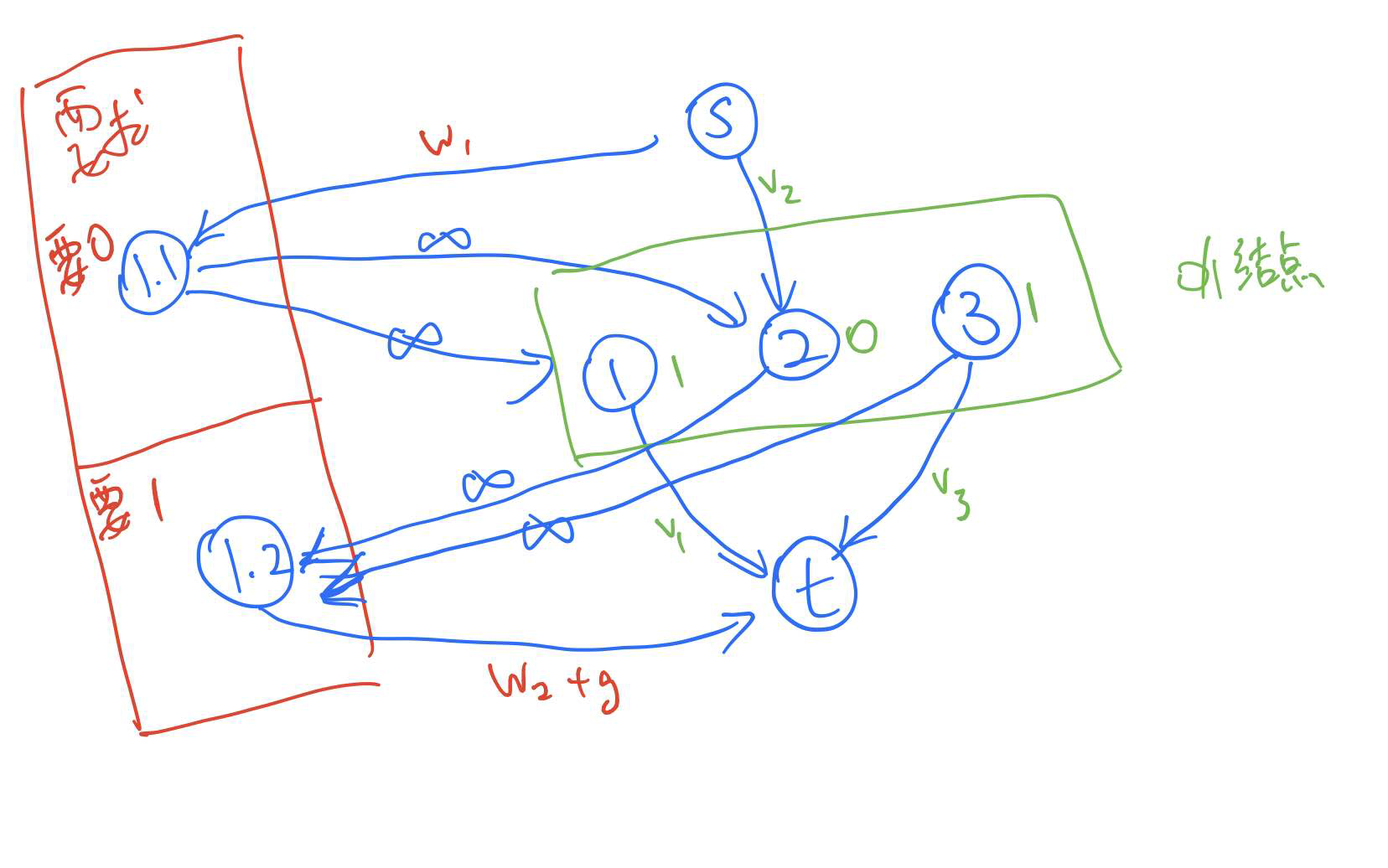
- 原始结点
如果一个点是1,那么向t连边,价值是转换的价值。如果一个点是0,就从s向它连边,价值也是对应转换的价值。
- 要求
如果是要0的要求,那么从起点向它连边权为对应收益的边,然后从该要求点向所有的有关节点连正无穷的边。
如果是要1的要求,那么从所有有关节点向它连正无穷的边,然后从该要求节点连向终点,价值为对应的收益。
如果一个要求不满足会扣钱,也就是说满足了是\(w_{i}\)的收益,没有满足时\(-g\) 的收益。两者差值是\(w_{i}+g\) ,所以它来作为边权。
例子:
一共3个节点分别是101,2个要求,第一个要求1和2是0,第二个要求2和3是1并且不满足要扣钱,那么可以画出下面的示意图
通过链式结构来实现:从多个选项只能选择一个
选择=切断与源点/汇点的联系
如果有2种选择,只能选其中一个。一种选择与源点连边,另一个与汇点连边。然后朋友之间的关系在中间互相连边
https://www.luogu.com.cn/problem/P2057
参考文献
《网络流理论与算法》第九章
https://www.luogu.com.cn/blog/akakw1/solution-cf311e
https://www.cnblogs.com/acha/p/6735037.html
网络流习题
二分+检查答案
1423B Valuable Paper
题意
一个二分图,每一条边有一个边权。在匹配成功的情况下,使得最大边权最小。
思路
二分枚举一个最大值,然后跑一边网络流是否可行。
代码
1 |
|


