线性代数重要概念

Matrix Algebra

列表示 \[ A=\left[\begin{array}{llll} \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_n \end{array}\right] \]

定理基本运算

Let $A,B,C$ be matrices of the same size, and $r,s$ be scalars

$A+B=B+A$
$(A+B)+C=A+(B+C)$
$A+0=A$
$r(A+B)=rA+rB$
$(r+s)A = rA + sA$
$r(sA)=(rs)A$

scalar 可以交换位置 \[ \lambda(\boldsymbol{B} \boldsymbol{C})=(\lambda \boldsymbol{B}) \boldsymbol{C}=\boldsymbol{B}(\lambda \boldsymbol{C})=(\boldsymbol{B} \boldsymbol{C}) \lambda, \quad \boldsymbol{B} \in \mathbb{R}^{m \times n}, \boldsymbol{C} \in \mathbb{R}^{n \times k} \] transpose 不影响 \[ (\lambda \boldsymbol{C})^{\top}=\boldsymbol{C}^{\top} \lambda^{\top}=\boldsymbol{C}^{\top} \lambda=\lambda \boldsymbol{C} \]

Matrix Multiplication

When matrix $B$ multiplies a vector $x$ , it transfer $x$ into vector $Bx$

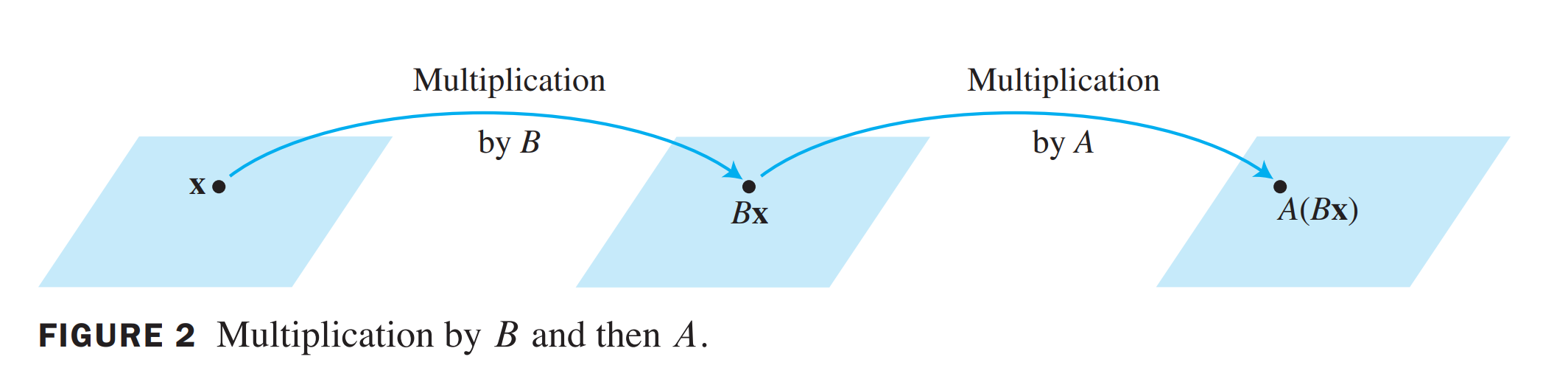\[ A(Bx)=(AB)x \] if $A$ is $m\times n$ , $B$ is $n \times p$ , and $x$ in $R^p$ \[ B \mathbf{x}=x_1 \mathbf{b}_1+\cdots+x_p \mathbf{b}_p \]

\[ \pi_U(\boldsymbol{x})=\sum_{i=1}^m \lambda_i \boldsymbol{b}_i=\boldsymbol{B} \boldsymbol{\lambda}, \]

\[ A B=A\left[\begin{array}{llll} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_p \end{array}\right]=\left[\begin{array}{llll} A \mathbf{b}_1 & A \mathbf{b}_2 & \cdots & A \mathbf{b}_p \end{array}\right] \]

\[ AD = [\lambda_1 A, \lambda_2 A, ... , \lambda_n A] \]

$D$ is diagoal

定理乘法的性质

$I_m$ is $m \times m$ identity matrix, $I_m \mathbf{x} = \mathbf{x}$ , $A$ is $m\times n$, $\mathbf{x}$ is in $\mathbb{R}^m$

$A(BC)=(AB)C$
$A(B+C)=AB+AC$
$(B+C)A=BA+CA$
$r(AB)=(rA)B=A(rB)$
$I_mA=A=AI_n$

The Transpose of a Matrix

$(A^T)^T=A$
$(A+B)^T=A^T + B^T$
$(rA)^T=r(A^T)$
$(AB)^T=B^TA^T$

inverse matrix

$A^{-1}A=AA^{-1}=I$
$(A^{-1})^{-1}=A$
$(AB)^{-1}=B^{-1}A^{-1}$
$(A^T)^{-1}= (A^{-1})^T$

vector space and subspaces

vector space

vector space is nonempty set $V$ of vectors.

两个向量相加在里面
和scalar 乘在里面
$0\in V$

subspace

vector space 且是另一个vector space 的子集

The Null Space of a Matrix

$Ax=0$ , the set of $x$ is the null space of $A$

Properties of Determinants

$A$ is invertible if and only if $det(A) \ne 0$
$det(AB) = det(A)det(B)$
$det(A^T)=det(A)$
if $A$ is triangular, $det(A)=$ product of entries in the main diagonal
Row replacement doesn't change determinant

Find span

Find span of mull space of the matrix $A=\left[\begin{array}{rrrrr}-3 & 6 & -1 & 1 & -7 \\ 1 & -2 & 2 & 3 & -1 \\ 2 & -4 & 5 & 8 & -4\end{array}\right]$

先化成 $\left[\begin{array}{rrrrrr}1 & -2 & 0 & -1 & 3 & 0 \\ 0 & 0 & 1 & 2 & -2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0\end{array}\right]$

然后列式子 \[ \begin{aligned} x_1-2 x_2-x_4+3 x_5 & =0 \\ x_3+2 x_4-2 x_5 & =0 \\ 0 & =0 \end{aligned} \] 所以看出 \[ \left[\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right]=\left[\begin{array}{c} 2 x_2+x_4-3 x_5 \\ x_2 \\ -2 x_4+2 x_5 \\ x_4 \\ x_5 \end{array}\right]=x_2\left[\begin{array}{l} 2 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right]+x_4\left[\begin{array}{r} 1 \\ 0 \\ -2 \\ 1 \\ 0 \end{array}\right]+x_5\left[\begin{array}{r} -3 \\ 0 \\ 2 \\ 0 \\ 1 \end{array}\right] \] 那些就是要求的 Base vectors

Rank

$\operatorname{rk}(\boldsymbol{A})=\operatorname{rk}\left(\boldsymbol{A}^{\top}\right)$ row rank = col rank
for square matrix $\boldsymbol{A}$ is regular (invertible) if and only if $\operatorname{rk}(\boldsymbol{A})=n$

Linear Mapping

\[ \forall \boldsymbol{x}, \boldsymbol{y} \in V \ \forall \lambda, \psi \in \mathbb{R}: \Phi(\lambda \boldsymbol{x}+\psi \boldsymbol{y})=\lambda \Phi(\boldsymbol{x})+\psi \Phi(\boldsymbol{y}) \]

we have to keep in mind what the matrix represents: a linear mapping or a collection of vectors

Image

\[ \operatorname{Im}(\Phi):=\Phi(V)=\{\boldsymbol{w} \in W \mid \exists \boldsymbol{v} \in V: \Phi(\boldsymbol{v})=\boldsymbol{w}\} \]

Null Space and Column Space

$\boldsymbol{A}=\left[\boldsymbol{a}_1, \ldots, \boldsymbol{a}_n\right]$, where $\boldsymbol{a}_i$ are the columns of $\boldsymbol{A}$, \[ \begin{aligned} \operatorname{Im}(\Phi) & =\left\{\boldsymbol{A} \boldsymbol{x}: \boldsymbol{x} \in \mathbb{R}^n\right\}=\left\{\sum_{i=1}^n x_i \boldsymbol{a}_i: x_1, \ldots, x_n \in \mathbb{R}\right\} \\ & =\operatorname{span}\left[\boldsymbol{a}_1, \ldots, \boldsymbol{a}_n\right] \subseteq \mathbb{R}^m \end{aligned} \]

\[ \operatorname{rk}(\boldsymbol{A})=\operatorname{dim}(\operatorname{Im}(\Phi)) \]

For vector spaces $V, W$ and linear mapping $\Phi: V \rightarrow W$ : \[ \operatorname{dim}(\operatorname{ker}(\Phi))+\operatorname{dim}(\operatorname{Im}(\Phi))=\operatorname{dim}(V) \]

Transformation Matrix

\[ \hat{\boldsymbol{y}}=\boldsymbol{A}_{\Phi} \hat{\boldsymbol{x}} \]

t the transformation matrix can be used to map coordinates with respect to an ordered basis in V to coordinates with respect to an ordered basis in W.

Traces

properties

\[ \operatorname{tr}(\boldsymbol{A}+\boldsymbol{B})=\operatorname{tr}(\boldsymbol{A})+\operatorname{tr}(\boldsymbol{B}) \text { for } \boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{n \times n} \]

\[ \operatorname{tr}(\alpha \boldsymbol{A})=\alpha \operatorname{tr}(\boldsymbol{A}), \alpha \in \mathbb{R} \text { for } \boldsymbol{A} \in \mathbb{R}^{n \times n} \]

\[ \operatorname{tr}\left(\boldsymbol{I}_n\right)=n \]

\[ \operatorname{tr}(\boldsymbol{A} \boldsymbol{B})=\operatorname{tr}(\boldsymbol{B} \boldsymbol{A}) \text { for } \boldsymbol{A} \in \mathbb{R}^{n \times k}, \boldsymbol{B} \in \mathbb{R}^{k \times n} \]

the trace is invariant under cyclic permutations \[ \operatorname{tr}(\boldsymbol{A} \boldsymbol{K} \boldsymbol{L})=\operatorname{tr}(\boldsymbol{K} \boldsymbol{L} \boldsymbol{A}) \]

\[ \operatorname{tr}\left(\boldsymbol{x} \boldsymbol{y}^{\top}\right)=\operatorname{tr}\left(\boldsymbol{y}^{\top} \boldsymbol{x}\right)=\boldsymbol{y}^{\top} \boldsymbol{x} \in \mathbb{R} \]

Eignevalue and Eigenvector

$\mathbf{x} \mapsto A \mathbf{x}$ 我们称之为一个变换，它会把vector $x$ 变成不同的方向，但是有一些 $x$ 很特殊，它的变换很简单, 比如

$A=\left[\begin{array}{rr}3 & -2 \\ 1 & 0\end{array}\right], \mathbf{u}=\left[\begin{array}{r}-1 \\ 1\end{array}\right]$, and $\mathbf{v}=\left[\begin{array}{l}2 \\ 1\end{array}\right]$

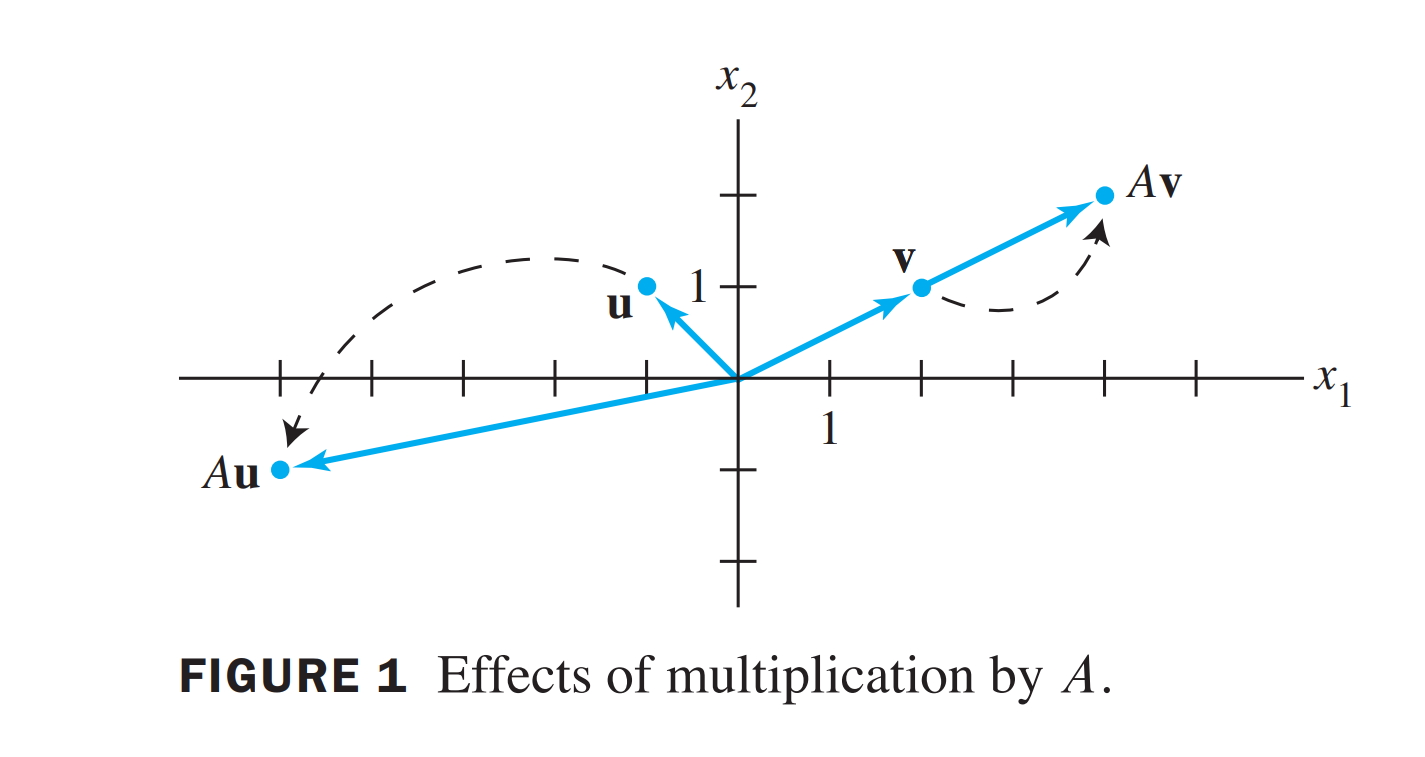
对于 $v$ 来说，只是伸展了。这里，我们研究那些只会伸展的向量

Eigenvector

matrix $A$ 的 eigenvector 是一个 non-zero vector $x$ 使得 $Ax=\lambda x$ A scalar is called an eigenvalue of A if there is a nontrivial solution $x$

The null space of $A-\lambda I$ is a subspace of $R^n$ and is called the eigenspace of $A$ corresponding to $\lambda$

the eigenspace corresponding to $\lambda=7$ consists of all multiples of $(1,1)$, which is the line through $(1,1)$ and the origin

在eigenspace上的向量eigenvector在$A$ 的变换下就是乘上 $\lambda$

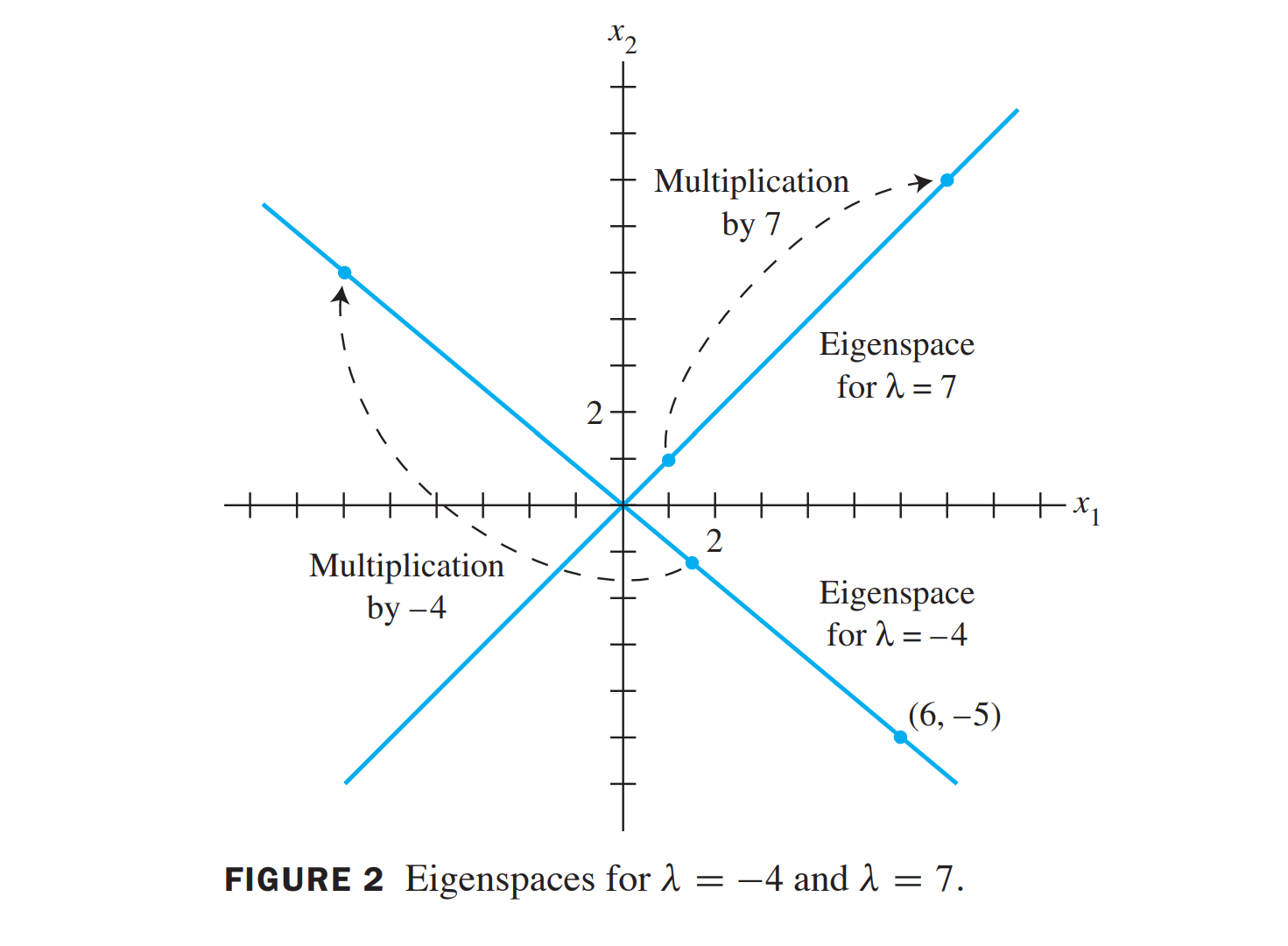
在三维的情况下，eigenspace 是过原点的二维平面

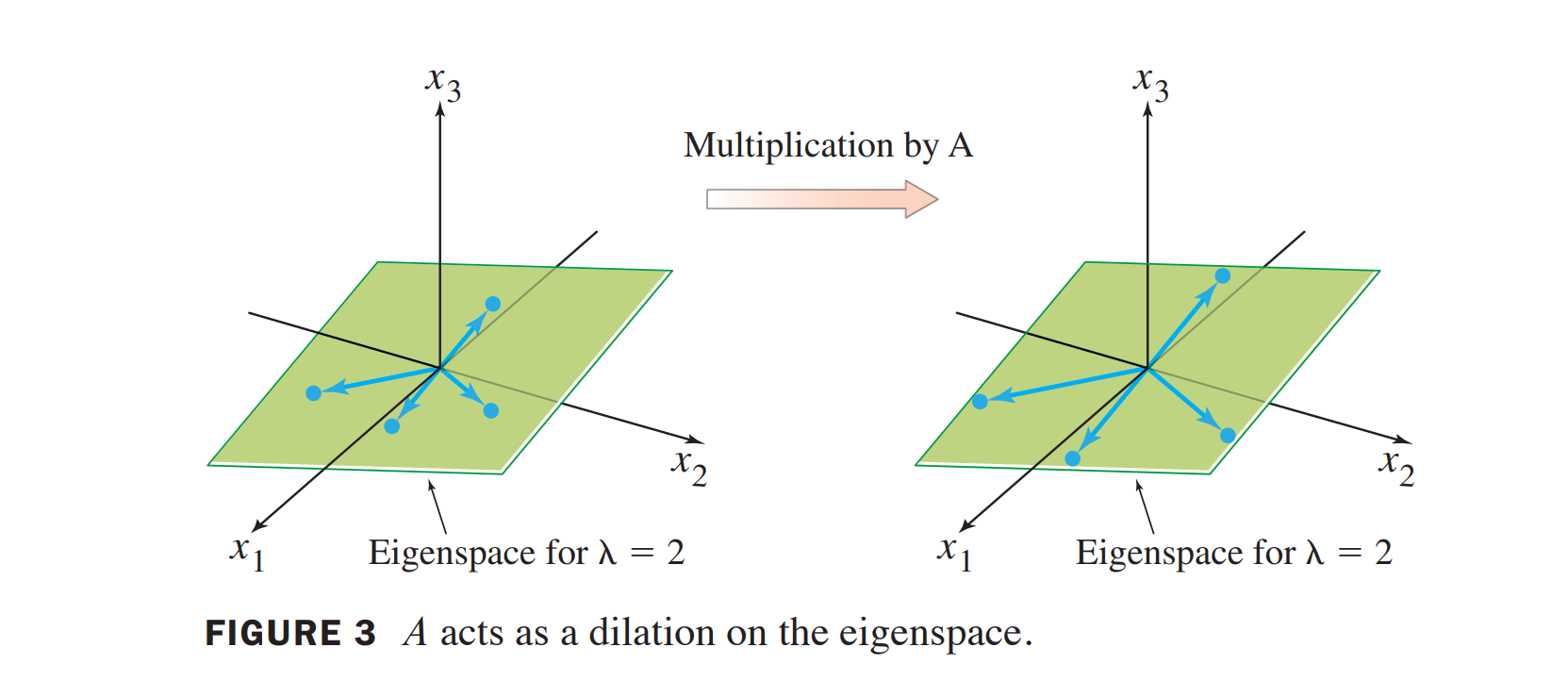
定理 eigenvalue of triangular matrix

The eigenvalues of a triangular matrix are the entries on its main in diagnoal

证明 \[ \begin{aligned} A-\lambda I & =\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array}\right]-\left[\begin{array}{ccc} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{array}\right] \\ & =\left[\begin{array}{ccc} a_{11}-\lambda & a_{12} & a_{13} \\ 0 & a_{22}-\lambda & a_{23} \\ 0 & 0 & a_{33}-\lambda \end{array}\right] \end{aligned} \] 当且仅当 $(A-\lambda I) \mathbf{x}=\mathbf{0}$ 有 non-trival 解的时候, $\lambda$ 才是 $A$ 的 eigenvalue. ($x \ne 0$ ) 这个时候肯定是列是线性相关的，不然解出来的 $x$ 肯定是 $0$ .也就是 $\lambda = a_{11},a_{22},a_{33}$ 的时候

结论 eigenvalue 0

0 is eigenvalue of $A$ if and only if $A$ is not invertible.

定理 linearly independence of eigenvector

If $\mathbf{v}_1, \ldots, \mathbf{v}_r$ are eignenvectors to distinct eigenvalues $\lambda_1, \ldots, \lambda_r$ of $A$ , then the vectors are linerly independent

证明

反证法：假设 $\mathbf{v}_1, \ldots, \mathbf{v}_r$ are eignenvectors 是 dependent, 那么 \[ c_1 \mathbf{v}_1+\cdots+c_p \mathbf{v}_p=\mathbf{v}_{p+1} \] 有因为 $Av=\lambda v$所以 \[ c_1 \lambda_1 \mathbf{v}_1+\cdots+c_p \lambda_p \mathbf{v}_p=\lambda_{p+1} \mathbf{v}_{p+1} \] 前一个式子乘 $\lambda{p+1}$ 然后相减得到 \[ c_1\left(\lambda_1-\lambda_{p+1}\right) \mathbf{v}_1+\cdots+c_p\left(\lambda_p-\lambda_{p+1}\right) \mathbf{v}_p=\mathbf{0} \] 因为$v_1,...,v_p$ 是 independent, 所以 $\lambda_i = \lambda_{p+1}$ 这和distinct $$ 矛盾了

Properties

symmetric

A matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ , $\boldsymbol{S}:=\boldsymbol{A}^{\top} \boldsymbol{A}$ $\in \mathbb{R}^{n \times n}$ is symmetric, positive semidefinite, if $\operatorname{rk}(\boldsymbol{A})=n$ then positive definite.

eigenvalues

The determinant of a matrix $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ is the product of eigenvalues \[ \operatorname{det}(\boldsymbol{A})=\prod_{i=1}^n \lambda_i \] The trace of a matrix $\boldsymbol{A} \in \mathbb{R}^{n \times n}$ is the sum of eigenvalues \[ \operatorname{tr}(\boldsymbol{A})=\sum_{i=1}^n \lambda_i \]

Similarity

$A,B$ are $n\times n$ matrices. $A$ is similar to $B$ if there is an invertible matrix $P$ such that $P^{-1}AP=B$ or $A=PBP^{-1}$ , Writing $Q=P^{-1}$ ,we have $Q^{-1}BQ=A$ . So $B$ is also similar to $A$

定理 similar and eigenvalue

if $A$ and $B$ are similar, then they have same characteristic polynomial and same eigenvalues

证明

$B-\lambda I = P^{-1}AP - \lambda I = P^{-1}AP - \lambda P^{-1}P = P^{-1}(AP-\lambda P) = P^{-1}(A-\lambda I) P$

$det(B-\lambda I) = det(P^{-1}) det(A-\lambda I) det(P) = det(A-\lambda I)$

Diagnoalization

To compute $A^k$ fast, we can decomposite $A=PDP^{-1}$

then $A^2 = (PDP^{-1})(PDP^{-1})= PD^2P^{-1}$ . 对于对角矩阵 $D$ , 它的幂是很好算的 \[ A^k=PD^kP^{-1} \]

定理 Diagnoalizable

A $n\times n$ matric $A$ is diagnoalizable if and only if $A$ has n linearly independent eigenvectors. This case, the columns of $P$ are $n$ linearly independent eigenvectors of $A$

证明

\[ A P=A\left[\begin{array}{llll} \mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_n \end{array}\right]=\left[\begin{array}{llll} A \mathbf{v}_1 & A \mathbf{v}_2 & \cdots & A \mathbf{v}_n \end{array}\right] \] with \[ P D=P\left[\begin{array}{cccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{array}\right]=\left[\begin{array}{llll} \lambda_1 \mathbf{v}_1 & \lambda_2 \mathbf{v}_2 & \cdots & \lambda_n \mathbf{v}_n \end{array}\right] \] Suppose $A$ diagnoalizable $A=PDP^{-1}$ Then $AP=PD$ then $A\mathbf{v_{i}}=\lambda_{i}\mathbf{v_i}$

推论

A $n\times n$ matric $A$ with $n$ distinct eigenvalues is diagnoalizable

The Matrix of a Linear Transformation

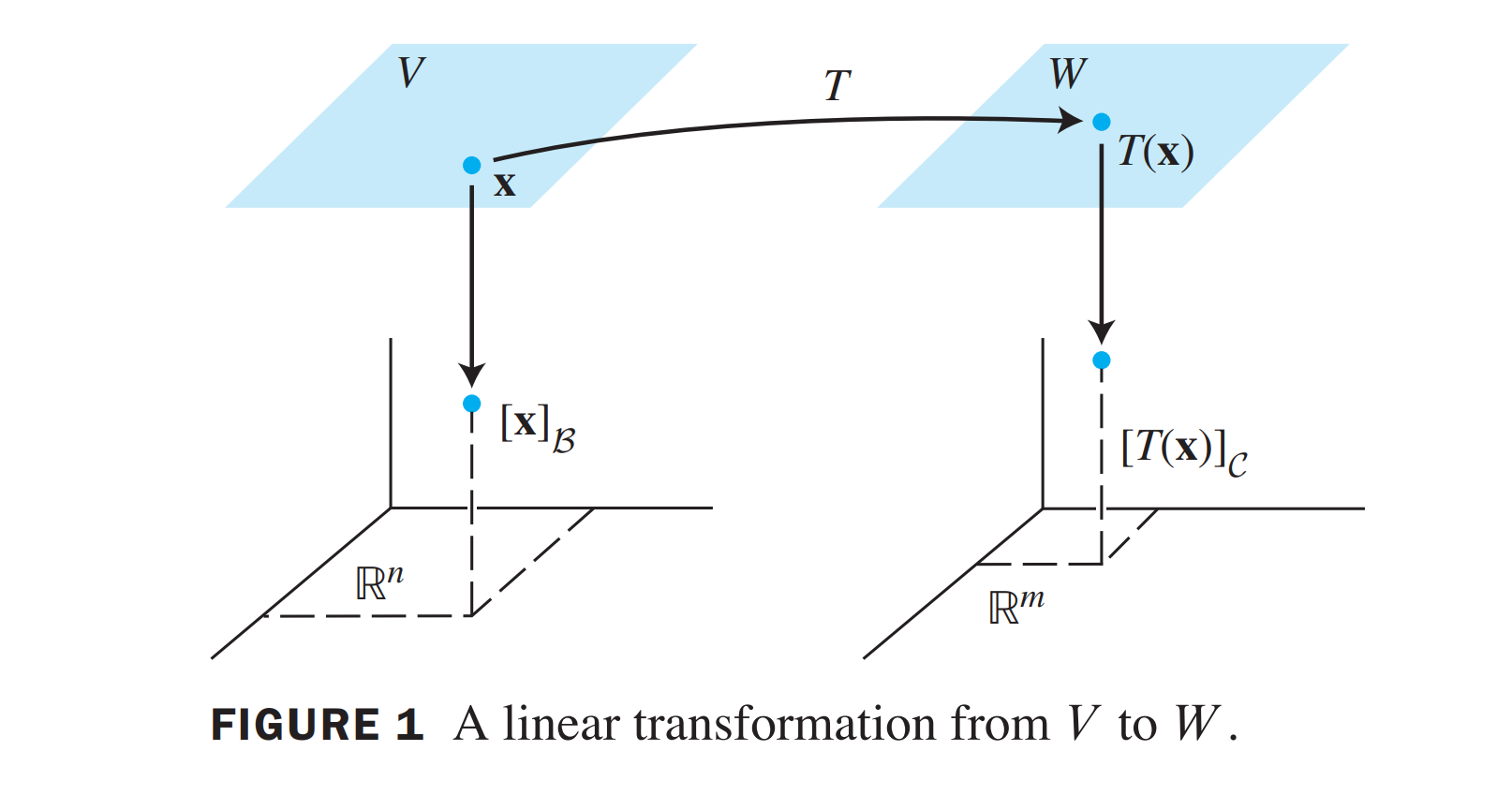
$T$ 是任意的Linear Transformation from $\mathcal{B}$ to $\mathcal{C}$

把 $\mathbf{x}$ 写成 Base $\mathcal{B}$ 的形式: \[ [\mathbf{x}]_{\mathcal{B}}=\left[\begin{array}{c} r_1 \\ \vdots \\ r_n \end{array}\right] \] 也就是 $\mathbf{x}=r_1 \mathbf{b}_1+\cdots+r_n \mathbf{b}_n$

那么可以计算 $T(\mathbf{x})$ \[ T(\mathbf{x})=T\left(r_1 \mathbf{b}_1+\cdots+r_n \mathbf{b}_n\right)=r_1 T\left(\mathbf{b}_1\right)+\cdots+r_n T\left(\mathbf{b}_n\right) \] 把它写成 base $\mathcal{C}$ 的形式 \[ [T(\mathbf{x})]_{\mathcal{C}}=r_1\left[T\left(\mathbf{b}_1\right)\right]_{\mathcal{C}}+\cdots+r_n\left[T\left(\mathbf{b}_n\right)\right]_{\mathcal{C}} \] 把这个变换写成矩阵的形式 \[ [T(\mathbf{x})]_{\mathcal{C}}=M[\mathbf{x}]_{\mathcal{B}} \]

\[ M=\left[\begin{array}{llll} {\left[T\left(\mathbf{b}_1\right)\right]_{\mathcal{C}}} & {\left[T\left(\mathbf{b}_2\right)\right]_{\mathcal{C}}} & \cdots & {\left[T\left(\mathbf{b}_n\right)\right]_{\mathcal{C}}} \end{array}\right] \]

$M$ 就是 matrix representation of $T$ relative to the bases $\mathcal{B}$ and $\mathcal{C}$

The Singular Value Decomposition

Orthonormal Sets

A set $\left\{\mathbf{u}_1, \ldots, \mathbf{u}_p\right\}$ is is an orthonormal set if it is an orthogonal set of unit vectors. 若 $W$ 是 subspace spanned by such a set，那么它是 $W$ 的 orthogonal basis.

定理 orthonormal columns

An $m \times n$ matrix $U$ has orthonormal columns if and only if $U^T U=I$

定理 orthonormal property

Let $U$ be an $m \times n$ matrix with orthonormal columns， let $\mathbf{x}$ and $\mathbf{y}$ be in $\mathbb{R}^n$

$\|U \mathbf{x}\|=\|\mathbf{x}\|$
$(U \mathbf{x}) \cdot(U \mathbf{y})=\mathbf{x} \cdot \mathbf{y}$
$(U \mathbf{x}) \cdot(U \mathbf{y})=0$ if and only if $\mathbf{x} \cdot \mathbf{y}=0$

This means that orthogonal matrices A with A ⊤ = A −1 preserve both angles and distances. It turns out that orthogonal matrices define transformations that are rotations (with the possibility of flips).

The absolute values of the eigenvalues

The singular value decomposition is based on the following property of the ordinary diagonalization that can be imitated for rectangular matrices: The absolute values of the eigenvalues of a symmetric matrix A measure the amounts that $A$ stretches or shrinks certain vectors (the eigenvectors).

If $A \mathbf{x}=\lambda \mathbf{x}$ and $\|\mathbf{x}\|=1$ then \[ \|A \mathbf{x}\|=\|\lambda \mathbf{x}\|=|\lambda|\|\mathbf{x}\|=|\lambda| \] 设 $A$ 是 $m \times n$ 矩阵， $A^TA$ 是 symmetric 并且可以 orthogonally diagonalized. 设 $\left\{\mathbf{v}_1, \ldots, \mathbf{v}_n\right\}$ 是 $A^TA$ 的由eigenvectors组成的 orthonormal basis , $\lambda_1, \ldots, \lambda_n$ 是对应的 eigenvalues. \[ \begin{aligned} \left\|A \mathbf{v}_i\right\|^2 &=\left(A \mathbf{v}_i\right)^T A \mathbf{v}_i=\mathbf{v}_i^T A^T A \mathbf{v}_i \\ & =\mathbf{v}_i^T\left(\lambda_i \mathbf{v}_i\right) \\ & =\lambda_i \quad \\ & \end{aligned} \] So the eigenvalues of $A^TA$ are all nonnegative

singular value

the singular values of A are the lengths of the vectors $A \mathbf{v}_1, \ldots, A \mathbf{v}_n$, 用 $\sigma_1, \ldots, \sigma_n$ 降序表示 $\sigma_i=\sqrt{\lambda_i}$ for $1 \leq i \leq n$

定理 orthonormal basis

若 $\left\{\mathbf{v}_1, \ldots, \mathbf{v}_n\right\}$ 是一个 orthonormal basis of $\mathbb{R}^n$ , 由 $A^TA$ 的 eigenvalues 组成，其中的eigenvalues 降序 $\lambda_1 \geq \cdots \geq \lambda_n$ 并且 $A$ 有 $r$ 个非零的 singular values. 那么 $\left\{A \mathbf{v}_1, \ldots, A \mathbf{v}_r\right\}$ 是 $\operatorname{Col} A$ 的 orthonormal basis 并且 $\operatorname{rank} A=r$

定理 The Singular Value Decomposition

Let $A$ be an $m \times n$ matrix with rank $r$. Then there exists an $m \times n$ matrix $\Sigma$ as $\Sigma=\left[\begin{array}{rr}D & 0 \\ 0 & 0\end{array}\right]$ which the diagonal entries in $D$ are the first $r$ singular values of $A$, $\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r>0$, and there exist an $m \times m$ orthogonal matrix $U$ and an $n \times n$ orthogonal matrix $V$ such that \[ A=U \Sigma V^T \]

Matrix Calculus

Gradients of Vectors

$f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}$ \[ \nabla_A f(A) \in \mathbb{R}^{m \times n}=\left[\begin{array}{cccc} \frac{\partial f(A)}{\partial A_{11}} & \frac{\partial f(A)}{\partial A_{12}} & \cdots & \frac{\partial f(A)}{\partial A_{1 n}} \\ \frac{\partial f(A)}{\partial A_{21}} & \frac{\partial f(A)}{\partial A_{22}} & \cdots & \frac{\partial f(A)}{\partial A_{2 n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f(A)}{\partial A_{m 1}} & \frac{\partial f(A)}{\partial A_{m 2}} & \cdots & \frac{\partial f(A)}{\partial A_{m n}} \end{array}\right] \]

\[ \nabla_x f(x)=\left[\begin{array}{c} \frac{\partial f(x)}{\partial x_1} \\ \frac{\partial f(x)}{\partial x_2} \\ \vdots \\ \frac{\partial f(x)}{\partial x_n} \end{array}\right] \]

For a function $\boldsymbol{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m$ and a vector $\boldsymbol{x}=\left[x_1, \ldots, x_n\right]^{\top} \in \mathbb{R}^n$ then the vector function \[ \boldsymbol{f}(\boldsymbol{x})=\left[\begin{array}{c} f_1(\boldsymbol{x}) \\ \vdots \\ f_m(\boldsymbol{x}) \end{array}\right] \in \mathbb{R}^m \] The gradient is \[ \frac{\partial \boldsymbol{f}}{\partial x_i}=\left[\begin{array}{c} \frac{\partial f_1}{\partial x_i} \\ \vdots \\ \frac{\partial f_m}{\partial x_i} \end{array}\right]=\left[\begin{array}{c} \lim _{h \rightarrow 0} \frac{f_1\left(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots x_n\right)-f_1(\boldsymbol{x})}{h} \\ \vdots \\ \lim _{h \rightarrow 0} \frac{f_m\left(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots x_n\right)-f_m(\boldsymbol{x})}{h} \end{array}\right] \in \mathbb{R}^m \] The Jacobian $\boldsymbol{J}$ is an $m \times n$ matrix \[ \begin{aligned} \boldsymbol{J} & =\nabla_{\boldsymbol{x}} \boldsymbol{f}=\frac{\mathrm{d} \boldsymbol{f}(\boldsymbol{x})}{\mathrm{d} \boldsymbol{x}}=\left[\begin{array}{ccc} \frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial x_1} & \ldots & \frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial x_n} \end{array}\right] \\ & =\left[\begin{array}{ccc} \frac{\partial f_1(\boldsymbol{x})}{\partial x_1} & \cdots & \frac{\partial f_1(\boldsymbol{x})}{\partial x_n} \\ \vdots & \vdots \\ \frac{\partial f_m(\boldsymbol{x})}{\partial x_1} & \ldots & \frac{\partial f_m(\boldsymbol{x})}{\partial x_n} \end{array}\right], \\ \boldsymbol{x} & =\left[\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right], \quad J(i, j)=\frac{\partial f_i}{\partial x_j} . \end{aligned} \] Consider \[ \boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A} \boldsymbol{x}, \quad \boldsymbol{f}(\boldsymbol{x}) \in \mathbb{R}^M, \quad \boldsymbol{A} \in \mathbb{R}^{M \times N}, \quad \boldsymbol{x} \in \mathbb{R}^N \]

\[ f_i(\boldsymbol{x})=\sum_{j=1}^N A_{i j} x_j \Longrightarrow \frac{\partial f_i}{\partial x_j}=A_{i j} \]

\[ \frac{\mathrm{d} \boldsymbol{f}}{\mathrm{d} \boldsymbol{x}}=\left[\begin{array}{ccc} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_N} \\ \vdots & & \vdots \\ \frac{\partial f_M}{\partial x_1} & \cdots & \frac{\partial f_M}{\partial x_N} \end{array}\right]=\left[\begin{array}{ccc} A_{11} & \cdots & A_{1 N} \\ \vdots & & \vdots \\ A_{M 1} & \cdots & A_{M N} \end{array}\right]=\boldsymbol{A} \in \mathbb{R}^{M \times N} \]