概率论

习题1

例1

A,B,C 三匹马比赛跑步，构造一个离散概率空间，使得事件“A比B快”，"B比C快"，“C比A快”出现的概率都大于 $1/2$

例2

已知带偶数条纹的斑马出现的概率是带奇数条纹斑马的2倍。设事件 $E_n$ 为随机选取一个斑马，发现它有数量为 $n$ 的条纹。构造一个离散概率空间，使得 $E_n$ 所有正整数的概率都大于0，且符合题意。

例3

现在要做 $m$ 个蓝莓蛋糕，一共有 $n$ 个蓝莓。现在把这 $n$ 个蓝莓等可能随机放到 $m$ 个蛋糕上。

求第 $i$ 个蛋糕没有蓝莓的概率
求所有蛋糕至少有 $1$ 个蓝莓的概率

例4

有一个幸运轮盘，上面写有 $1$ 至 $125$ 的数字（包含1和125），每一个数字等可能出现

求转出的数字是4的倍数或者是平方数的概率
转出的数，每位上数字的和大于3的概率

例5

A，B，C轮流扔硬币（从A开始），硬币是正面的概率是 $0<p<1$ ，第1次扔到反面的人赢。求A，B，C各自赢的概率

例6

有 $n$ 份没有名字的作业。把这 $n$ 份作业随机分发到这 $n$ 个人上（每个人随机发一份），那么没有一个人拿到自己作业的概率是多少。

例7

有一个鬼在路上吓人，设事件 $E_n$ 为这个鬼刚好吓到了 $n$ 个人。对于 $n>0$ 满足 \[ Pr[E_n]=\frac{Pr[E_{n-1}]}{n} \] 求这个鬼一个人都没有吓到的概率

习题2

例1

女生A，B，C和男生D，E，F随机分成3个2人学习小组。每种分配概率相等。

证明一共有15种分配情况
求所有小组是一男一女组合的概率
已知A和D一组，求所有小组是一男一女组合的概率
证明或证伪：事件” ‘A和D一组’与‘B和C一组’的并集“和“所有小组是一男一女组合的”是不相干事件(unabhängig)

例2

A扔硬币 $n$ 次（扔出正面概率为$1/2$），($n \ge 2$) 设 $E$ 是事件：同时出现扔出正面和扔出反面的情况。设 $F$ : 正面扔出最多1次。若 $E$ ,$F$ 不相干，求 $n$ 的值

例3

给定树 $B_n$ ，其中$B_n(n>1)$ 的左边是 $B_{n-2}$, 右边是 $B_{n-1}$，一个蚂蚁从树根开始往叶子走（不能回头，等可能随机走）

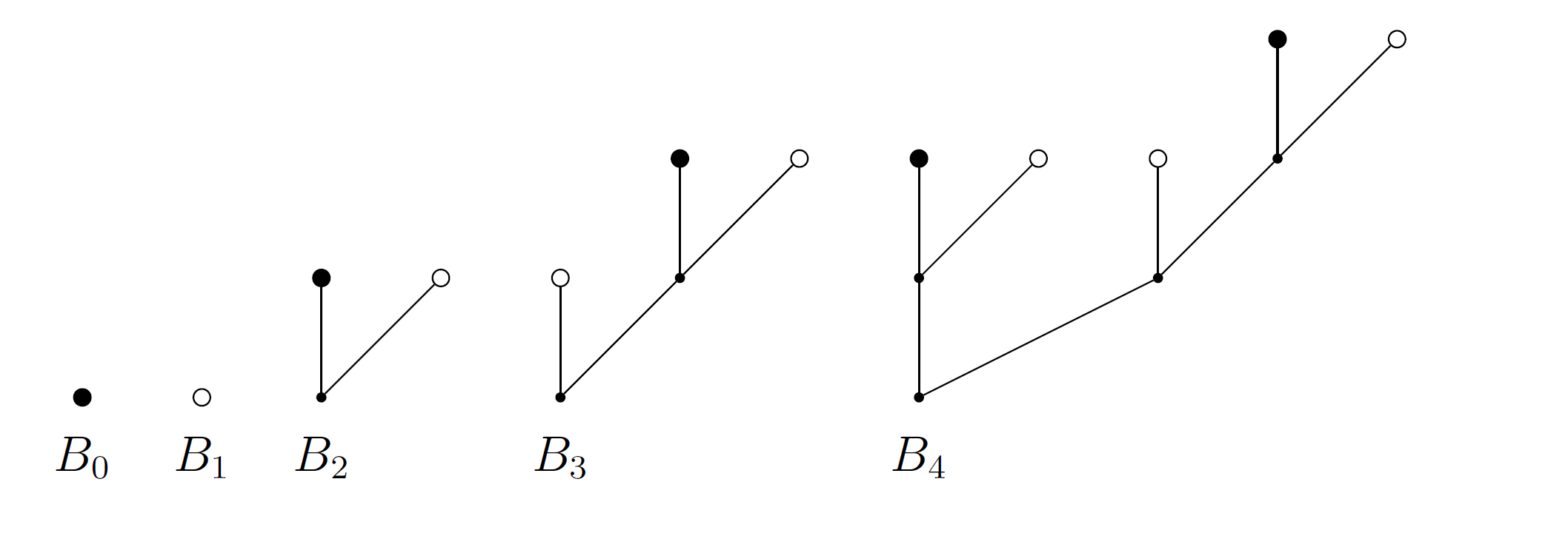
证明它在白色叶子节点结束的概为 \[ Pr[E_n]=\frac{2}{3}(1-(-\frac{1}{2})^n) \]

例4

A买了4个蓝莓蛋糕，已知卖家分别有 $1/8,1/16,1/6,1/4$ 的概率在 $1,2,3,4$ 个蛋糕里都放蓝莓。

求超过一半的蛋糕有蓝莓的概率
已知A随机打开一个蛋糕时，发现里面有蓝莓。求上一问的概率

例5

把数字 $1,3,4,4,7,8$ 填入下面的6个格子里

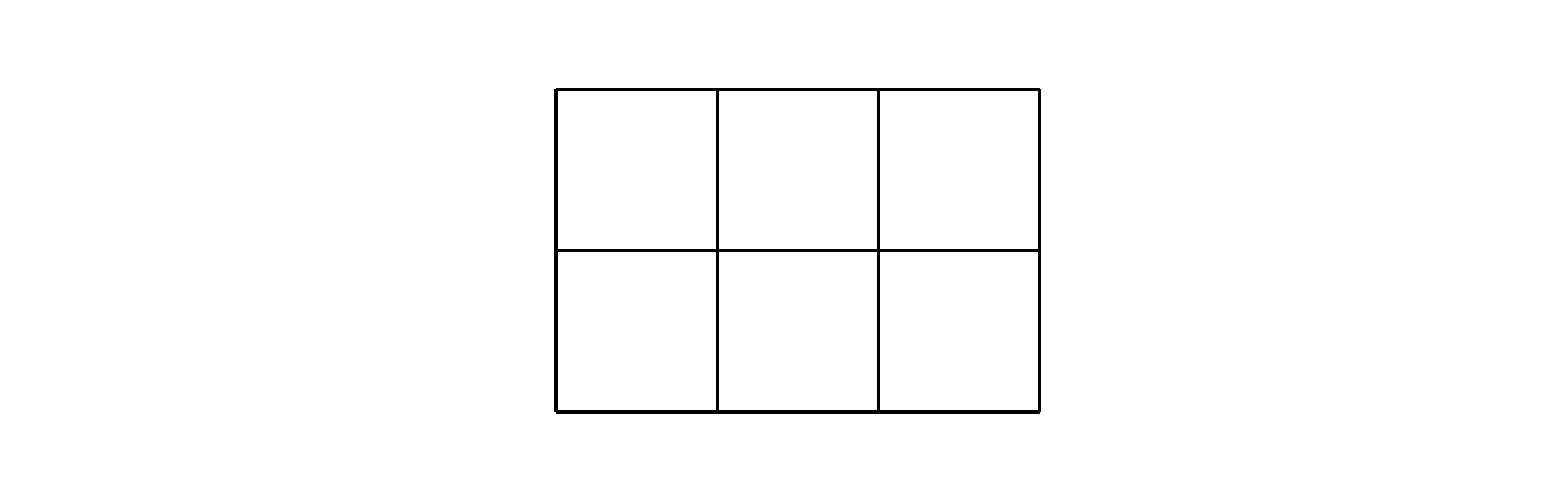
求离散概率空间 $\Omega$ 的大小
求2个4填在同一行的概率
若已知上面的3个格子里有4和8，求上面3个格子的数字和小于下面3个格子数字和的概率

例6

现有45个球上分别有 $1...45$ 的编号，还有4个盒子。

先在第1个盒子里是数字能被3整除的球
然后再把剩下偶数的球放到第2个盒子
然后再把剩下质数的球放到第3个盒子
然后把剩下的放到第4个盒子

现在随机选一个盒子，然后从这个盒子随机选一个球。

设$E$ 是事件：选出的球编号小于10，求 $E$ 的概率
设 $F$ 是事件：选出的球是质数。证明或证伪：$E$ 和$F$ 不相干(unabhängig)。

例7

考虑离散概率空间 $\Omega$

设事件 $A,B \subseteq \Omega$ ，$A \subset B$ . 什么时候 $A,B$ 不相干。
设事件 $C,D \subseteq \Omega$ ，$Pr[D]>0$ 且 $Pr[C|D]>Pr[C]$. 证明或者证伪：$Pr[C|\bar{D}] < Pr[C]$
对于一个事件族群 $(E_i)_{i\in \N}$ 是两两不相干的，若对于所有不同的下标 $i \ne j$ ，事件 $E_i,E_j$ 不相干。证明或证伪：一个两两不相干的事件族群中的事件是互不相干的。

习题3

例1

考虑一个三维的单位立方体。我们随机选取一个顶点。设 $X:\{0,1\}^3 \rightarrow \R$ 是从顶点$a$ 映射到欧几里得模 $X(a)=\|a\|_{2}$ 的随机变量。求 $X$ 的概率密度函数，分布，期望和方差。

例2

A和B交替扔一个均匀的硬币($1/2$ 概率正面)，直到第1次出现正面。设 $n$ 是游戏的回合数，赢的人会获得 $2^n/n$ 元钱。A 先开始。

设 $X$ 是A的收益，如果输的话收益是负数。证明： $X$ 的期望不存在
构造一个赢钱的方式，使得 A的收益的期望存在，但是方差不存在

例3

现有 $n$ 张卡片，每一张的两面写着 $2^{i-1}$ 和 $2^i$. 现在将卡片重新洗牌，设第1张牌正面是随机变量 $X$ 映射的数。

求 $X$ 的期望，若卡片等可能随机出现
如果你可以获得这张牌等额的钱，并且你有一次机会把牌的反面翻过来。证明：你有一种策略使得你期望获得多于 $\mathbb{E}[X]$ 的钱。

例4

天气有3种变化:晴，多云，大风。设 $X$ 是在某一天出现天气个数的随机变量。已知 $\mathbb{E}[X]=3/2$ .求3个天气在一天同时出现概率的取值范围。

例5

在盒子里有7个球，分别标有O，S，O，R，E，I，N，这几个字母，且每个球都有生产编号。现在从盒子里不放回拿取球，直到抽出2个O。设 $X$ 是抽取次数的随机变量

求$X$的值域，概率密度函数和分布. 把概率密度函数化简成 $f_X(k)=(k-a)/b, k\in W_X$ 的形式
计算 $X$ 的期望和方差

例6

一个图上有 $n=4$ 个点，现在随机在图中添加无向边。每个节点对的概率是不相干的，且都分别有 $p=1/2$ 的概率被添加边。设 $X:\Omega \rightarrow [4]$ 是联通分量的个数的随机变量。求 $X$ 的期望和标准差

例7

A和B在比赛跑步。他们扔一个正常的硬币(1/2概率)决定谁往前走1cm，正面A走，反面B走。最先甩开对手 4cm的获胜。设 $X$ 是优胜者总共向前移动的厘米数。

设 $E$ 是事件，A和B在2轮后在相同位置。设 $F$ 和 $G$ 分别是事件： A在2轮后甩开对手2cm 和 B 在2轮后甩开对手 2cm. 求 $\mathbb{E}[X|E],\mathbb{E}[X|F],\mathbb{E}[X|G]$ 用 $E[X]$ 表示即可。
根据1的式子求 $\mathbb{E}[X]$

习题4

A给学生布置3道题，每解出一题得1分。若答案错误不得分。已知学生随机拿分。设 $X_i$ 是第 $i$ 道题的得分。且 \[ f_{X_{1}, X_{2}, X_{3}}\left(x_{1}, x_{2}, x_{3}\right)=\left\{\begin{array}{ll} \left(x_{1}+x_{2}+x_{3}-1\right)^{2} / 8 & \text { für } x_{1}, x_{2}, x_{3} \in\{0,1\} \\ 0 & \text { sonst } \end{array}\right. \] 是概率密度函数

求边缘密度 $f_{X_1},f_{X_2}$ 和 $f_{X_3}$
这些变量是$X_i$独立(unabhangig)的吗
计算总分的期望和方差

例2

已知排列 $\pi:[n+2] \rightarrow[n+2]$,。如果排列 $\pi$ 是随机的，若$i\in[2,n+1]$ 满足 $\pi(i-1)>\pi(i)<\pi(i+1)$ ，求 $i$ 的个数的期望。

例3

写着 $n$ 个数的幸运轮盘(等概率)，设 $X,Y$ 是两个相互独立的随机变量(unabhängig) 对应A和B转出来的结果。若 $X \ge Y$ 那么 A从B那里得到$X-Y$ 的分数，若 $Y>X$ 那么B从A那里得到 $Y-X$ 的分数。设 $Z=X-Y$ 是A的收益/亏损。求 $Z$ 的概率密度函数。

例4

从一副扑克牌中随机抽取3张，设 $X$ 是不同花色的随机比哪里，$Y$是不同点数的随机变量。求边缘概率密度 $f_X,f_Y$ 和总概率密度函数 $f_{X,Y}$

例5

设 $X_1 ... X_n$ 是随机变量， $f_1 ... f_n$ 是任意实数函数。证明或证伪： $X_1,...X_n$相互独立，当且仅当 $f(X_1),...f(X_n)$ 相互独立。

例6

从 $n$ 个球(编号$1..n$)的袋子里，不放回抽取球。若当前抽取的球的编号小于之前抽取的球的编号时结束。求抽取次数的期望。

例7

设 $X,Y$ 是随机变量 \[ f_{X}(x)=f_{Y}(x)=\left\{\begin{array}{ll} \left(\frac{1}{2}\right)^{x-c} & \text { falls } x \in\{5,6, \ldots\} \\ 0 & \text { sonst } \end{array}\right. \] $c \in \N$

求 $c$ 的值
求 $Z=X+Y$ 的概率密度函数

习题5

例1

A每天抓 $X$ 个虫子，$X$ 是服从参数为$\lambda > 0$ 泊松分布的随机变量。A只有 $0<p\le1$ 的概率抓住一只虫子。设$Y$ 是抓住虫子的数量，求$Y$ 的分布和期望

例2

A在等车，车期望会在 $\mu$ 分钟内来。设 $X$ 是A的等待时间，$X$ 服从几何分布。在 $i$ 分钟后,A会失去耐心并询问剩余等待时间 $X-i$ ，证明A的期望的等待时间仍然是 $\mu$, 即证明 $\mathbb{E}[X-i|X>i]=\mu$

例3

森林里一共 $n$ 只虫子, A要抓住并且研究 $m$ 只不同的虫子。已知A每抓1只并研究好后会将它放回森林，且A每天会以独立相同的概率抓这 $n$ 只虫子。

设 $X_i$ 是第 $i$ 只虫子被研究的次数。求 $X_i$ 的期望
若有些虫子可以藏起来不被研究，使得森林里的虫子总数量为 $k\ge m$ 。且在同样 $k$ 的条件下，每个虫子隐藏起来的概率相同。求 $k$ , 使得 $X_i$ 最小化

例4

用放射性光线照射 $10^9$ 个细菌。每个细菌的变异是相互独立的，概率为 $3/10^9$. 设 $X$ 是变异细菌的个数。

求 $X$ 的概率密度函数，期望和方差
用泊松分布近似求 $Pr[X\ge5]$

例5

A 从不同的公司叫了 $n$ 辆车，并搭乘最早来的一辆。第$i$ 辆车的等待时间是 $X_i$ ，服从参数为 $p_i$ 的几何分布。$X_i$ 是相互独立的，证明 $Y=min\{X_1,...,X_n\}$ 也服从几何分布，并求参数.

例6

A队和B队比赛。设 $X$ 是A的进球数，$Y$是B的进球数。已知$X$ 服从参数为 $\lambda$ 的泊松分布。且 $Y$ 的概率密度函数是 \[ f_{Y}(y)=\left\{\begin{array}{ll} \frac{1}{(y+1)(y+2)} & \text { wenn } y \in \mathbb{N}_{0} \\ 0 & \text { sonst. } \end{array}\right. \]

求 $B$ 有可能进至少2球的概率
判断 $Y$ 的期望是否存在
求比赛平局结束的概率

例7

对于离散随机变量 $X$ ，若分布满足 \[ f_{X}\left(x^{*}\right)=\max _{x \in \mathbb{R}} f_{X}(x)\] ,那么 \[x^{*} \in \R\] 为模态值，求

参数为 $\lambda>0$ 泊松分布的模态值
参数为$n\in\N,p\in(0,1)$二项分布的模态值

习题6

例1

设 $X$ 是随机变量 $W_X \in \N_0$ 我们考虑马尔可夫不等式 \[ \operatorname{Pr}[X \geq t] \leq \frac{\mathbb{E}[X]}{t}, \forall t\in \R, t > 0 \] 我们说它严格，若存在 $t>0$ 使得等式成立。证明：

存在一个分布，使得这个不等式的严格。
若 $X$ 有2个不同的取值 $a,b \in \N$, 且每个概率都大于0时，这个不等式不严格。

例2

A扔硬币 $a,b$ 两个硬币是相同的，除了 $a$ 正面的概率是 $3/4$, $b$ 正面的概率是 $1/4$ 但是 A忘记了哪个是哪个。若 A 随机选一个硬币并且扔 $99$ 次。使用切尔诺夫不等式，证明 A 判断正确的概率不小于 $99/100$

已知： $e^{101 / 4}>9 \cdot 10^{10}$ , $(297 / 196)^{196 / 4}<9 \cdot 10^{8}$.

例3

A在树林里捕捉虫子。在第1个下雨天之后，他的捕猎行动开始。假设每天都是独立的有 $0<p<1$ 的概率是下雨天。设第 $i$ 天捉到的虫子是 $Y_i$ ，是独立的以 $\lambda=-\ln(1-p)$ 泊松分布的随机变量。设 $X$ 是A总共捕猎的时间（包含第1个下雨天）。

设 $Z=\sum_{i=1}^{X}Y_i$ 是总捕捉虫子。求概率生成函数 $G_Z$
求 $\mathbb{E}[Z]$ . 证明 $\mathbb{E}[Z]=\mathbb{E}[X] \cdot \mathbb{E}[Y]$ , $Y$ 是以泊松分布的随机变量。

例4

$n$ 份作业随机发给这 $n$ 个学生。估计至少 $n/2$ 个学生拿到自己的作业的概率

使用马尔科夫不等式
使用切比雪夫不等式

例5

聚会中 A 邀请了32 个人，每个人出现的概率是独立的 $3/5$. A要给每个人烤一个蛋糕。使用切尔诺夫界求A应该烤几个蛋糕使得不够的概率最多 $1/10$

例6

已知 \[ G_{X}(s)=\exp \left(8 \cdot\left(s^{2}-1\right)\right) \]

求$X$ 的期望和方差
用切比雪夫不等式证明，$X \ge 32$ 的概率最多 $1/8$
设$M_X$ 是 $X$ 的秩生成函数 , $t > 0, s \ge 0$ 证明

\[ \operatorname{Pr}[X \geq t] \leq \frac{M_{X}(s)}{\exp (s \cdot t)} \]

例7

设 $X$ 是随机变量， $W_{X} \subseteq \mathbb{N}_{0}$ , $G_X$ 是对应的概率生成函数。设 $E$ 是事件：$X$ 是偶数

证明：$\operatorname{Pr}[E]=\frac{1+G_{X}(-1)}{2}$
设 $X$ 是二项分布，几何分布或泊松分布时，求使得$\operatorname{Pr}[E]>\operatorname{Pr}[\bar{E}]$ 的条件

习题7

例1

A一直扔一个硬币。设 $\Omega$ 是所有无穷扔硬币结果序列的集合。

证明 $\Omega$ 不可数
设 $\mathcal{A}$ 是包含所有 $A\subseteq \Omega$ 的集合，其中$A$ 满足：要么 $A$ 可数，要么$\Omega \setminus A$ 可数。证明 $\mathcal{A}$ 是 $\sigma$-代数
求一个合适的概率测度 $Pr$ 关于 $\mathcal{A}$ ，使得 $Pr$ 满足柯尔莫哥洛夫公理(Kolmogorov-Axiome)

例2

已知 $X$ 是连续的随机变量，$c>0$ \[ f_{X}(x)=\left\{\begin{array}{ll} c \cdot\left(1-x^{4}\right) & \text { 若 } x \in[-1,1] \\ 0 & \text { 其他 } \end{array}\right. \]

证明 $f_X$ 波莱尔可测(Borel-messbar)
求 $c$
计算 $X$ 的期望和方差

例3

设 $X$ 是连续随机变量并且有分布函数 \[ F_{X}(x)=\left\{\begin{array}{ll} 0 & \text { falls } x \leq 0 \\ x & \text { falls } 0<x \leq \frac{1}{2} \\ \frac{1}{2} & \text { falls } \frac{1}{2}<x \leq \ln (2) \\ 1-e^{-x} & \text { falls } x>\ln (2) \end{array}\right. \]

证明 $F_X$ 是分布函数
求对应的概率密度函数

例4

设 $\Omega$ 是全集，$\mathcal{M} \subseteq \mathcal{P}(\Omega)$ . 在所有由 $\mathcal{M}$ 产生的 $\sigma$ 代数中，$\sigma(\mathcal{M})$ 表示最小的$\sigma$ 代数。$\Omega=\{1,2,3,4\}$,$\mathcal{M}=\{\{1,2\},\{2,4\}\}$ 求$\sigma(\mathcal{M})$

例5

有一个长为 $l$ 的巧克力，A把它随机在 $X$ 处切成2半。设 $Y$ 是小的那一半的长度，$X$ 是 $(0,l)$ 的均匀分布。

求 $Y$ 的分布
求 $Y$ 的概率密度函数和期望

例6

已知连续随机变量 $X$ \[ F_{X}(x)=1 /\left(1+e^{-x}\right) \]

求 $f_X$ 并证明 $f_X(-x) = f_X(x)$
求 $-X$ 的密度函数
求 $X$ 的期望，已知期望存在

例7

用在 $(0,1)$ 上均匀分布的随机变量 $U$ 模拟随机变量 $X$

$X$ 是以 $\lambda>0$ 的指数分布
$X$ 在 $[a,b]$ 上均匀分布

习题8

例1

有一个球，设 $|X|$ 是球的半径， $X$ 是正态分布随机变量且期望$\mu=0$, 标准差 $\sigma=\sqrt{\pi / 2}$

求 $|X|$ 的密度函数
球的期望半径是 $1$, 那么半径的方差是多少
求的半径大于 $\pi / \sqrt{2}$ 的概率是多少

\[ \begin{array}{l|cccccc} x & \sqrt{\pi} / 2 & \sqrt{\pi / 2} & \sqrt{\pi} & \pi / 2 & \pi / \sqrt{2} & \pi \\ \hline \Phi(x) & 0,812 & 0,895 & 0,962 & 0,942 & 0,987 & 0,999 \end{array} \]

例2

设 $X$ 是指数分布的随机变量 $\lambda>0$. 设 $Y=e^{\alpha \cdot X}$ 其中 $\alpha >0$.

求 $Y$ 的密度函数
对于哪些 $\alpha$ 使得 $Y$ 的期望存在

例3

已知 \[ f_{X, Y}(x, y)=\left\{\begin{array}{ll} c & x^{2}+y^{2} \leq 1 \\ 0 & \text { sonst. } \end{array}\right. \]

求 $c$，已知 $\frac{1}{2} \cdot\left(\sqrt{1-y^{2}} \cdot y+\arcsin y\right)$ 是 $\sqrt{1-y^{2}}$ 的原函数
求总概率密度函数 $f_{X,Y}$ 的边缘密度函数 $f_X,f_Y$
$X,Y$ 是独立的吗

例4

$X$ 是正态分布的随机变量, 期望为 $5$, 方差为 $0.25$

把 $X$ 转换成标准正态分布 $Y$

\[ Z=\left\{\begin{array}{ll} 1 & 4.5 \le X \le 5.5 \\ 2 & X > 5.5 \\ 0 & \text { sonst. } \end{array}\right. \]

求 $Z$ 的概率密度函数和期望

例5

高为 $X$, 底为 $Y$ 的三角形如图

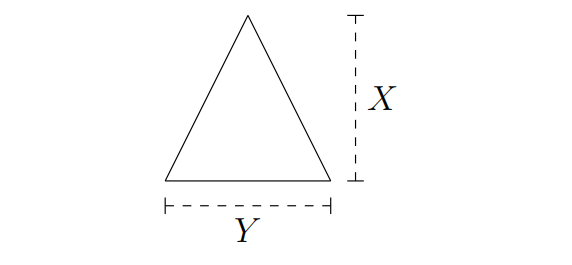
已知 $X-99$ 和 $Y-99$ 是两个独立的 $\lambda =1$ 的指数分布

求 $X$ 的概率密度函数
求 $min\{X,Y\}>100$ 的概率
求三角形面积的期望

例6 \[ f_{X, Y}(x, y)=\frac{\exp \left(-2 / 3 \cdot\left(x^{2}-x \cdot y+y^{2}\right)\right)}{2 \pi \cdot \sqrt{3 / 4}} \]

证明 $X,Y$ 是标准正态分布
$X,Y$ 是独立的吗

例7

A每次遇到1只灰色的兔子要等待 $X$ 分钟，每次遇到 1 只白色的兔子要等待 $Y$ 分钟。已知 $X$ 是期望为 $15$ 的指数分布随机变量，$Y$ 是期望为 $45$ 的指数分布随机变量，$X,Y$ 是独立的

求等到第1只兔子的期望等待时间
求需要等待多少时间，使得期望遇到兔子的总数为 $20$

习题9

例1

已知一共有 $10^6$ 个斑马。每个斑马独立有 $2/3$ 的概率有偶数条纹。设 $X$ 是偶数条纹斑马的数量

对于标准正态分布，证明 $-\Phi(-x)=\Phi(x)-1$
用中心极限独立估计一个尽可能小的区间，使得$Pr[aXb] $ 约为 $9/10$ 的，已知 $\Phi(\sqrt{2}) \approx 19 / 20$

例2

$X$ 和 $Y$ 是独立的标准正态分布，已知$Z=X^2 + Y^2$ 。求 $Z$ 的概率密度函数。已知$\int_{0}^{\alpha} 1 /(\sqrt{t \cdot(\alpha-t)}) d t=\pi$ 对于 $\alpha>0$

例3

已知对数正态分布： \[ f_{X}(x)=\left\{\begin{array}{ll} \frac{1}{\sqrt{2 \pi} \sigma x} \cdot \exp \left(-\frac{(\ln (x)-\mu)^{2}}{2 \sigma^{2}}\right) & \text { für } x>0 \\ 0 & \text { sonst } \end{array}\right. \]

求 $Y= \ln(X)$ 是以 $\mu$ 和 $\sigma$ 为参数的正态分布
通过秩生成函数求 $X$ 的期望

例4

已知 $X,Y$ 是在 $[0,1]$ 上独立均匀分布的随机变量

已知 $\int_{0}^{1} f_{Y}(x-z) \mathrm{d} x=1-|z|$ 对于 $|z| \leq 1$ ，求 $Z=X-Y$ 的概率密度和分布
求 $|Z| \le 1/4$ 的概率

例5

放射性光线照射 $2000$ 个细菌，每个细菌有独立 $5\%$ 的概率变异。求最多 $6$ 个细菌变异的概率

精确求
用泊松分布近似
用中心极限定理近似

例6

$X_1, ... X_n$ 是独立且相同的且值域是正数的随机变量。证明 $\prod_{i=1}^{n} X_{i}$ 是对数正态分布(若 $Y=ln(X)$ 是正态分布，则 $X$ 是对数正态分布)

例7

设 $X$ 是 $\lambda > 0$ 为参数的指数分布

求秩生成函数 $M_X$
已知：$M_{X}^{(k)}(0)=\mathbb{E}\left[X^{k}\right]$ ($a^{(k)}$ 是 $a$ 的 $k$ 阶导数)，求$X$ 的方差。

习题10

例1

A射$n$ 只箭。设 $X_i$ 是独立的相同分布的随机变量。其中期望和标准差未知。$Y=\sum_{i=1}^{n}\lambda_i \cdot X_i$ 是一个凸组合.

证明 $Y$ 对于期望 $\mu$ 是一个无偏估计量
证明 $1 / n \cdot \sum_{i=1}^{n} \lambda_{i}^{2} \geq 1 / n^{2}$
求 $\lambda _i$ 使得 $Y$ 的效率最优

例2

设 $X_1,X_2, ... , X_n$ 是独立的假设检验，其中 $\lambda >0$ 是未知指数分布 $X$ 的参数。求估计量 $Y$ 对于$\lambda$ 的最大似然估计

例3

独立的随机变量 $X_1,...X_n$ 是在 $[0,m]$ 上的均匀分布。

求 $c$ 使得带权样本均值 $c \cdot\left(\sum_{i=1}^{n} X_{i}\right) / n$ 是一个关于 $m$ 的无偏估计量
构造一个对最大似然估计的比较，这个估计量是无偏的吗

例4

已知： \[ f_{X_{n}}(x)=\left\{\begin{array}{ll} \left(\begin{array}{c} x+n-1 \\ x \end{array}\right) \cdot p^{n} \cdot(1-p)^{x} & \text { für } x \in \mathbb{N}_{0} \\ 0 & \text { sonst. } \end{array}\right. \] 其中 $0<p<1$ , 构造一个关于 $1/p$ 的无偏估计量.

例5

设 $X_1,...,X_n$ 是独立的对于随机变量 $X$ 的样本变量。求关于下面参数的最大似然估计

$X$ 是泊松分布，$\lambda>0$
$X$ 几何分布 $p\in(0,1)$

并且指出每一个情况的估计量是否是无偏的

例6

设 $X_1, .. X_n$ 是独立的指数分布的样本变量，$\lambda>0$

求关于 $1/\lambda$ 的最大似然估计量$Z$

例7

有编号 $1...n$ 的车辆，车辆编号等概率出现。设A在路上观测5辆车，看到最大的车辆编号为$X$.

估计量 $U_1=X,U_2= \lceil c \cdot X\rceil$ 其中 $c>0$ 是常数。

求尽可能小的 $c$, 使得 $n\in [U_1,U_2]$ 置信水平是 $0.9$

习题11

例1

一共有 $n$ 天，A估计平均温度为 $\bar{X}$ 度。$X$ 是正太分布，现在有未知的期望 $\mu$ 和标准差 $\sigma = 2$. 每天的温度用随机变量 $X_i$ 表示

求 $n$ 的下界，使得 $\bar{X}$ 有置信水平 $0.9$ 时 $\bar{X}$ 和 $\mu$ 相差不超过 $1$
若 $n=100$, 求尽可能小的置信区间

例2

有一个球，$p$ 的概率是黑色，$1-p$ 的概率是白色的。已知 $p$ 要么是 $H_0:1/4$ 要么是 $ H_1:3/4$. 为了验证，A生成了 $n$ 个求，其中有 $X$ 个是白色的

设 $K \in \{0,...,n\}$ 是$H_0$的拒绝域，该怎么选取 $K$ 使得1类错误和2类错误的和最小。
假设 A 拒绝了 $H_0$ , 用切诺夫界求 $n$ ，使得1类错误小于 $0.05$. (已知$(e / 4)^{8}<0,05$)

例3

一个药在 $n=100$ 个人上使用，已知对每个人的治愈概率为 $p\ge 0.9$ . 构造一个显著性差异为 $\%5$ 的假设验证，使得有最大的拒绝域

例4

已知一个盒子里独立有 $p$ 的概率有巧克力。A选了4个盒子，要验证每两个盒子里会有一个巧克力还是每3个盒子里有一个巧克力。若拒绝域是 $K\in \{0,1\}$ 求假设出错的概率

例5

每个细菌有 $0\le p \le 1$ 的概率。 A猜测 $p \le 2/100$ 并且要验证。现在有 $10000$ 个细菌。已知拒绝域为 $K = \{222,...10000\}$ . 求这个假设验证的显著性差异

例6

为了验证一个骰子扔出 $6$ 的概率是不是 $1/3$ 。A扔了 $100$ 次，结果如下： \[ \begin{array}{r|cccccc} \text { 数字 } & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \text { 次数 } & 13 & 10 & 14 & 18 & 15 & 30 \end{array} \] 已知除了点数 $6$ 扔出其他点数的概率相同。构造一个显著性差异达到 $0.01$ 的假设验证

已知 $\chi_{k, \alpha}^{2} = k \cdot\left(1-(2 /(9 k))+z_{\alpha} \cdot \sqrt{2 /(9 k)}\right)^{3}$

例7

A要比较两种瓜，每种选取 $16$ 个。已知瓜的口味是独立的正态分布的随机变量 $X_i$ 和 $Y_i$ . 构造一个合适的假设验证两种瓜的期望，使得显著性差异为 $0.01$ \[ \begin{array}{c|cccccccccccccccc} i & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \hline X_{i} & -1 & 0 & 1 & 1 & 2 & -1 & 4 & 3 & -1 & -2 & 1 & 4 & 2 & -1 & 4 & 2 \\ Y_{i} & -4 & -3 & -2 & 0 & -2 & -2 & 3 & 0 & 0 & -3 & -4 & 0 & -1 & -2 & 0 & 2 \end{array} \] 已知 $t_{k,\alpha}$ 当 $k \ge 30$ 时可以用 $z_{\alpha}$ 渐进

习题12

例1

有三个格子,A每天以相同的概率前进1格或者退后1格。若他在第1格后退或在第3格前进则结束。

用马尔可夫链建模
若A在中间的格子，求再次返回中间格的概率
问结束的期望时间

例2

有黄蓝红红4朵花，一只蜜蜂在花上飞但是每次不连续呆同一种颜色的花。他在飞之前决定飞往哪朵花且这几花概率相同。

设 $X_t$ 是飞到的第 $t$-朵花。求马尔可夫链的 $(X_t)_{t\ge 0}$ 传递图和开始分布. 开始随机等概率出现在这4朵花上
求稳定分布( stationären Verteilung)，并确定唯一性

例3

已知马尔可夫链 $0\le r \le 1$

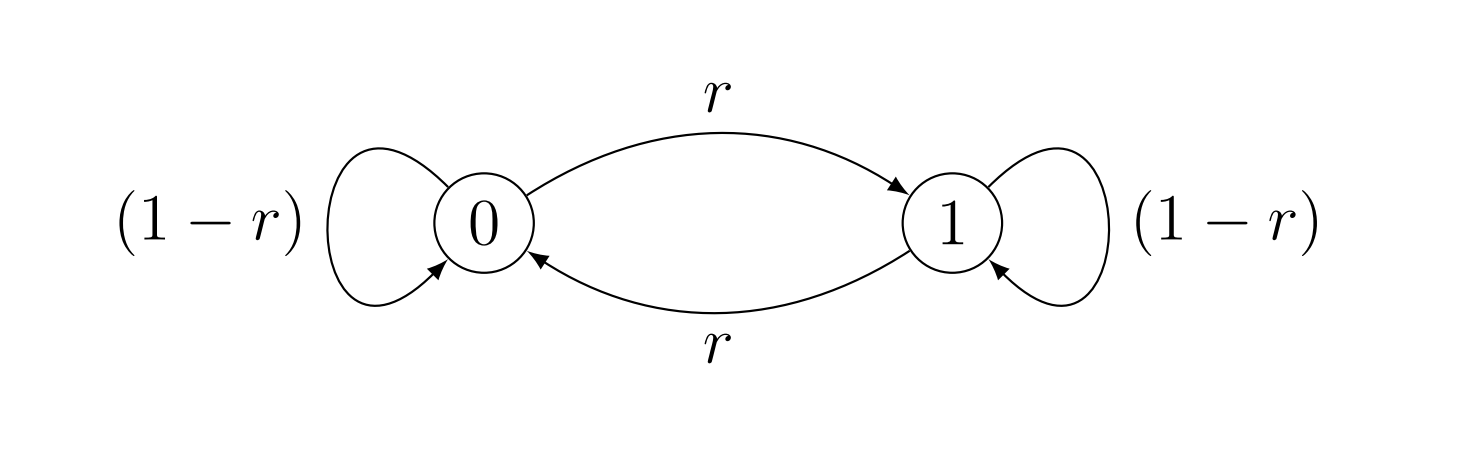
怎么选取 $r$ 使得马尔可夫链是非周期(aperiodisch)，不可简化(irreduzibel)，可遍历的(ergodisch)
对于哪些 $r$ 存在 $\pi$ 使得$\lim _{t \rightarrow \infty} p_{i, j}^{(t)}=\pi_{j}$ 对于所有 $i,j \in \{0,1\}$ 成立

例4

一共 $n$ 只动物，每只动物等概率出现，A要给每个动物拍照片。设 $X_t$ 是拍了 $t$ 张照片后还要拍的动物数量

用马尔可夫链建模 $(X_t)_{t\ge 0}$
判断非周期性(aperiodisch)，不可简化(irreduzibel)和可遍历(ergodisch)
设 $n=3$ 求拍完照片期望次数

例5

有4个房间，相邻房间等概率进入

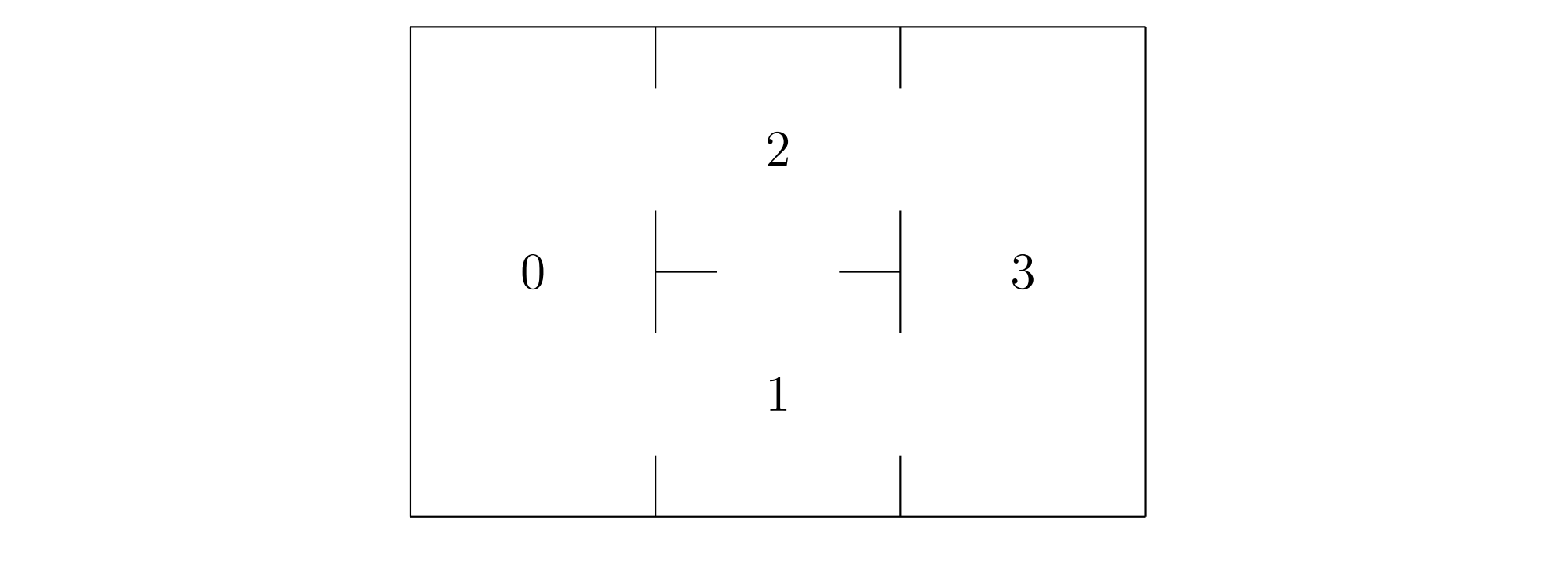
用马尔可夫链建模，$X_t$ 是 $t$ 时刻所在的房间编号
求 $\lim _{t \rightarrow \infty} q_{t}$ 的最小概率的房间号

例6

一个关于骰子的游戏，A开始一直扔，如果A扔出了一个偶数那么换B扔，如果A连续扔出3个奇数那么A胜利。B扔1次，如果扔出的是6那么B胜利，否则换A扔。

用马尔可夫链建模
求 A 赢的概率
求游戏结束的期望轮数

例7

设 $(Y_i)_{i\ge 0}$ 是一组独立的随机变量，值要么是 $1$ 要么是 $-1$ 每种值的概率相等，设 $X_{t}=\left(\sum_{i=0}^{t} Y_{i}\right) \bmod 4$ . 考虑马尔可夫链 $(X_t)$

求对应的传递图
判断不可简化性(irreduzibel)和非周期性(aperiodisch)
求所有的稳定分布( stationären Verteilungen)