数据库 | Hexo

引入

如果不使用数据库系统，会有很多问题，如数据的损失，多用户同时访问，安全问题，高昂的开发成本等。

数据库的结构

下面是一个数据库的示意图。最底层的是物理层，数据和数据结构(B树) 就存在这里。然后上面一层逻辑层是比如说放表格这些的位置。然后上面是不同的人相对于数据库不同的视角，因为权限不一样所以可以访问的也不一样

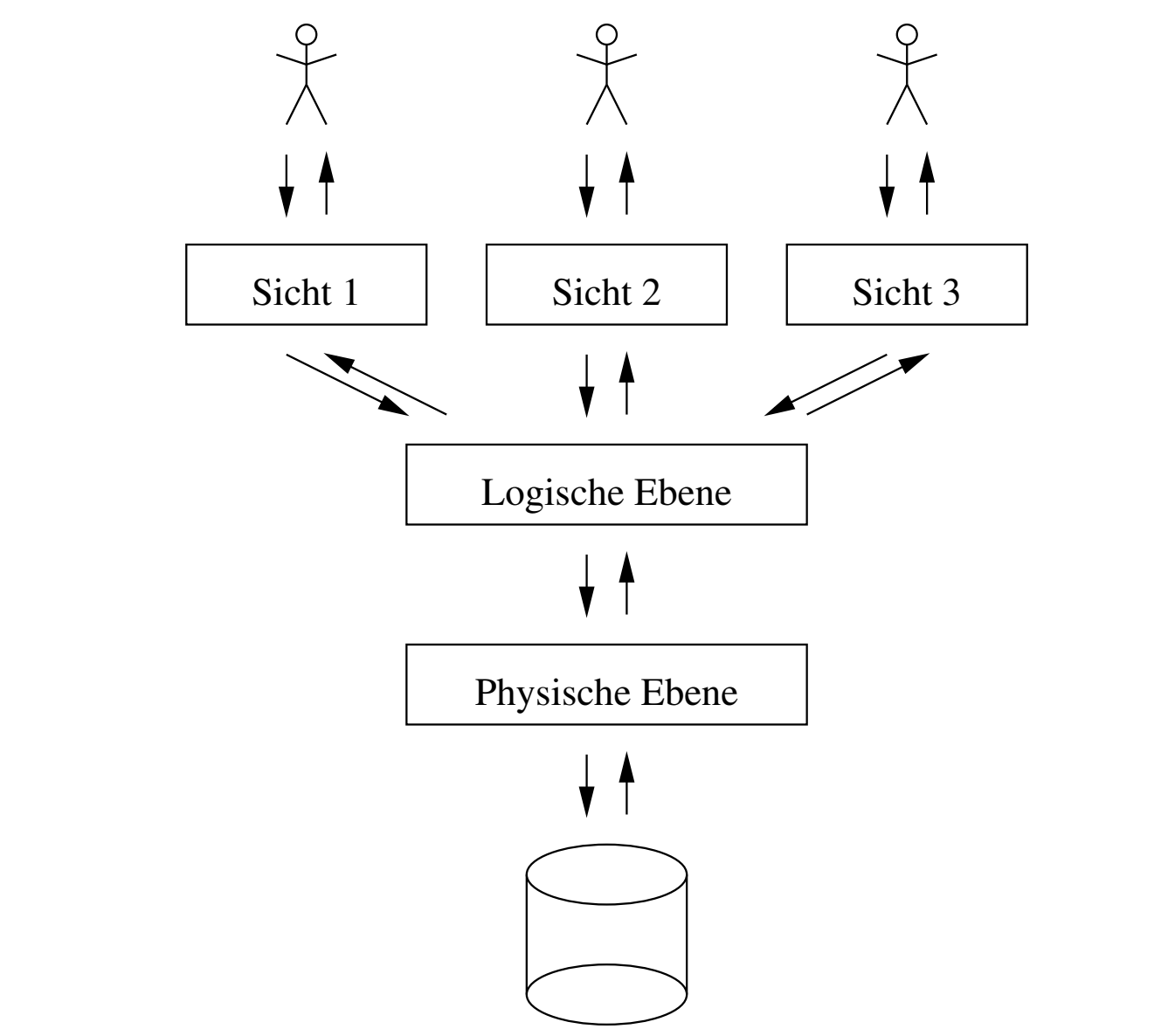
更为具体的是下面这张图

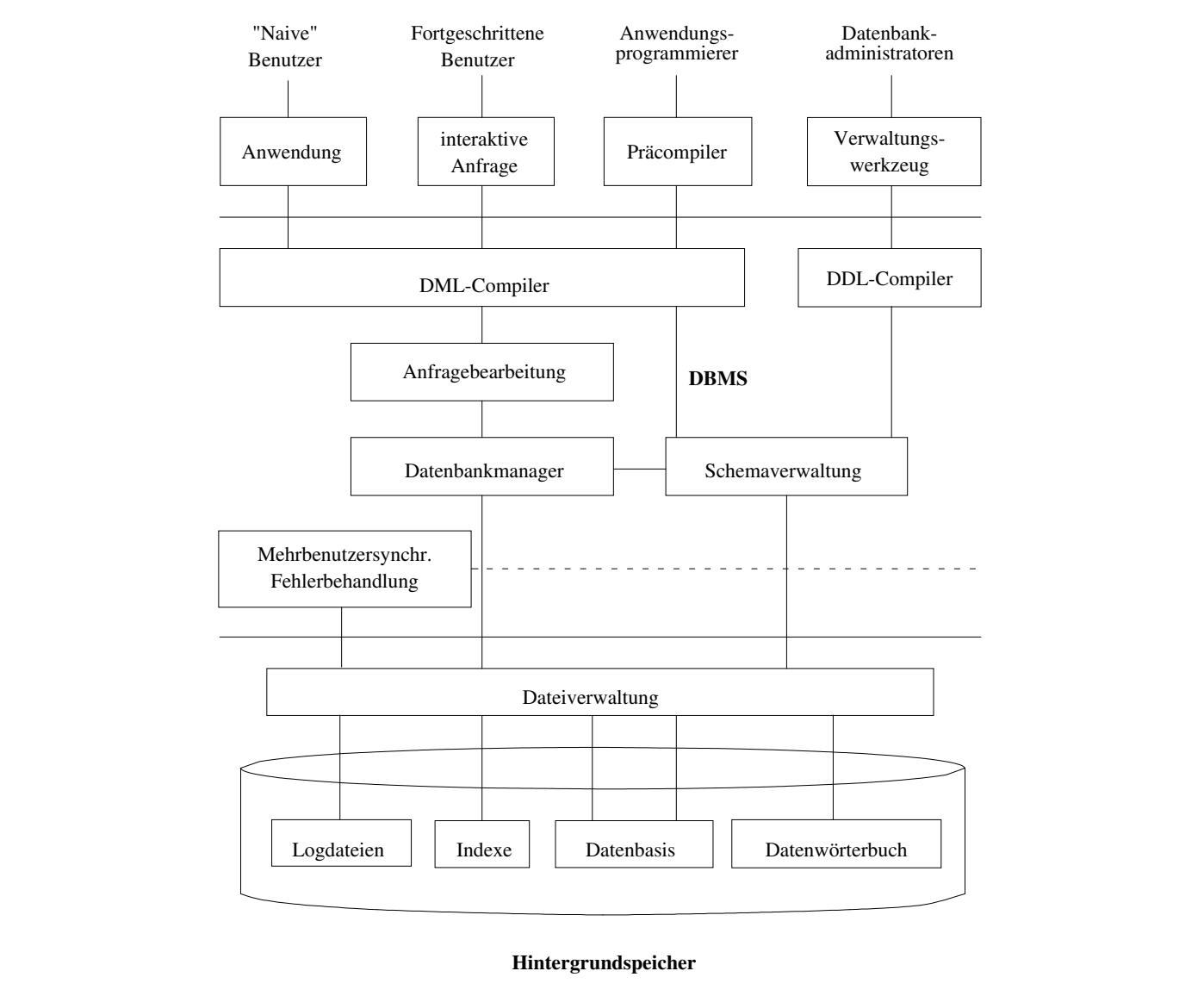
数据建模

类似我们在程序设计的时候要建模，在设计数据库的时候也要对数据建模，对于数据的概念模型有：

Entity-Relationship-Modell (ER-Modell)
Unified Modeling Language(UML)

逻辑层面的模型有

Relationales Modell 同过关系来建模

比如在大学的范围里，我们可以建立下面的数据模型

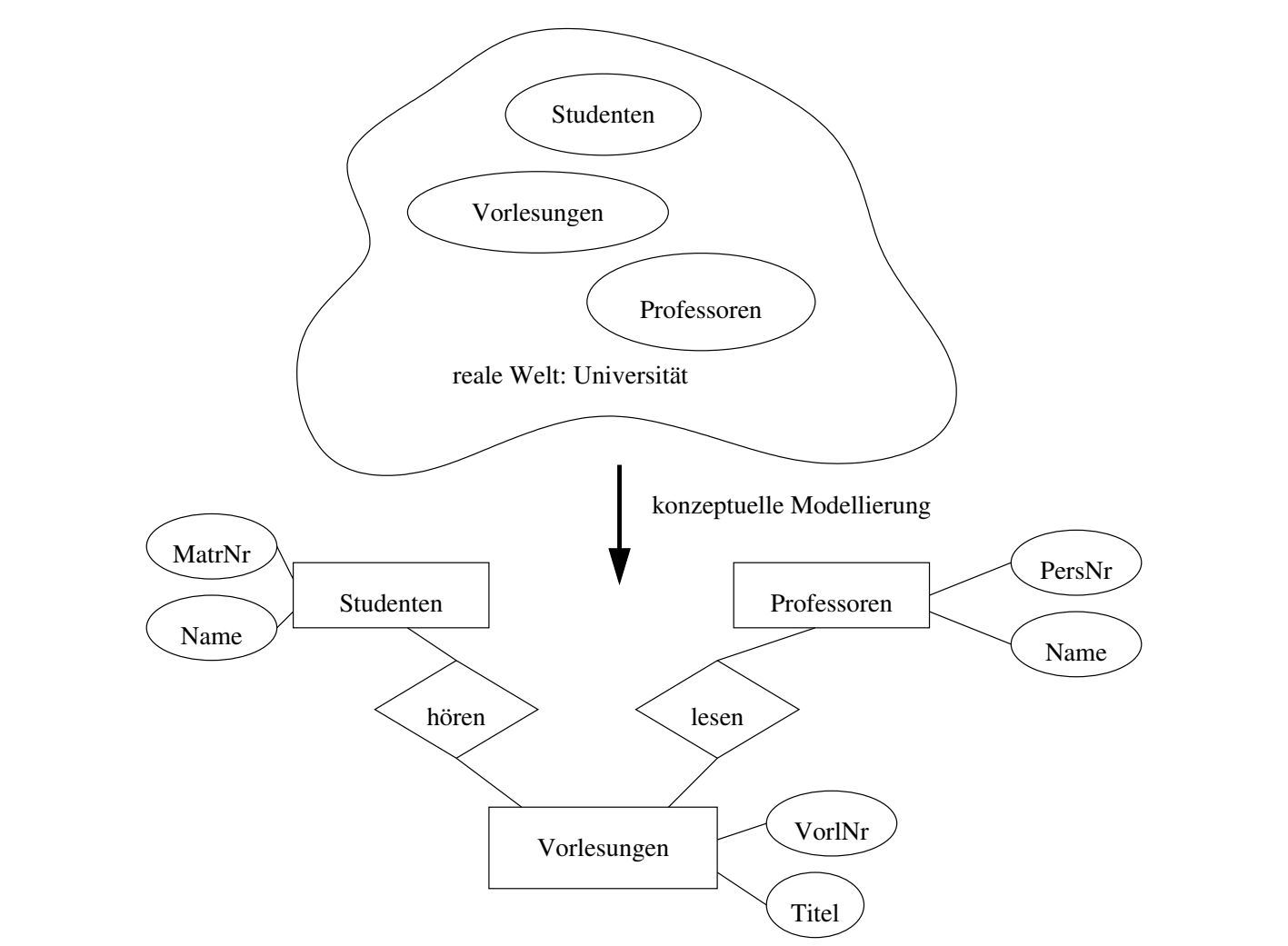
下面是对应的数据表

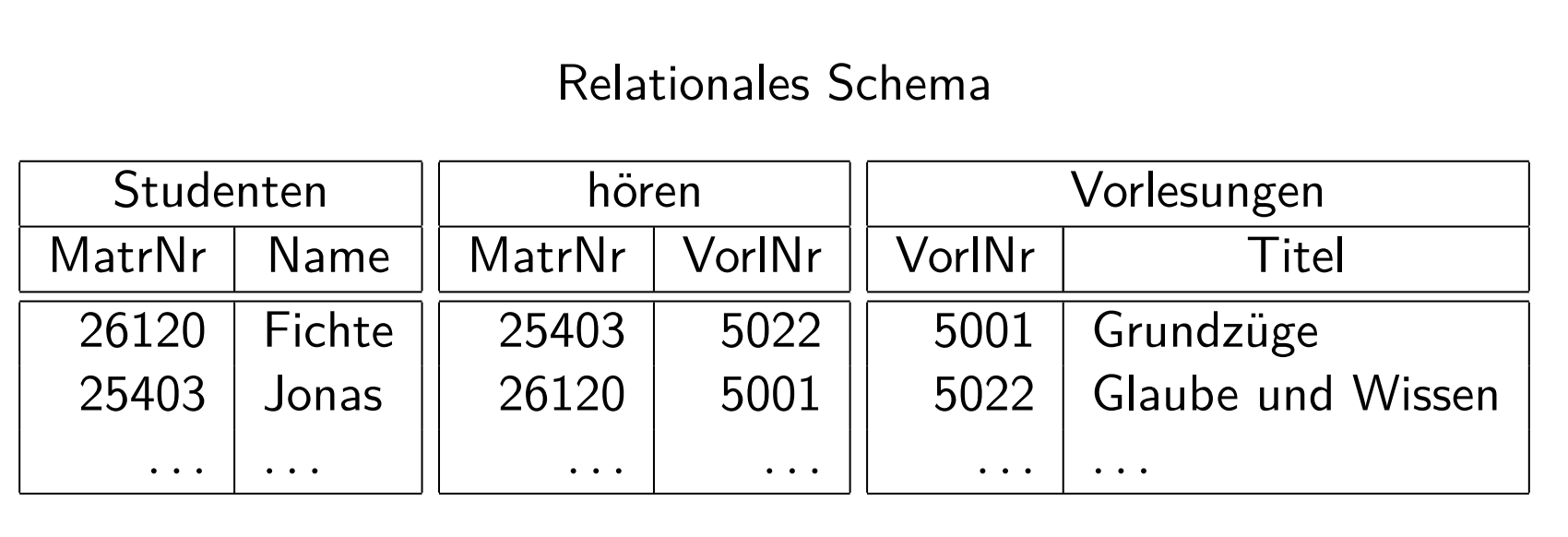
数据库设计

数据库设计的过程

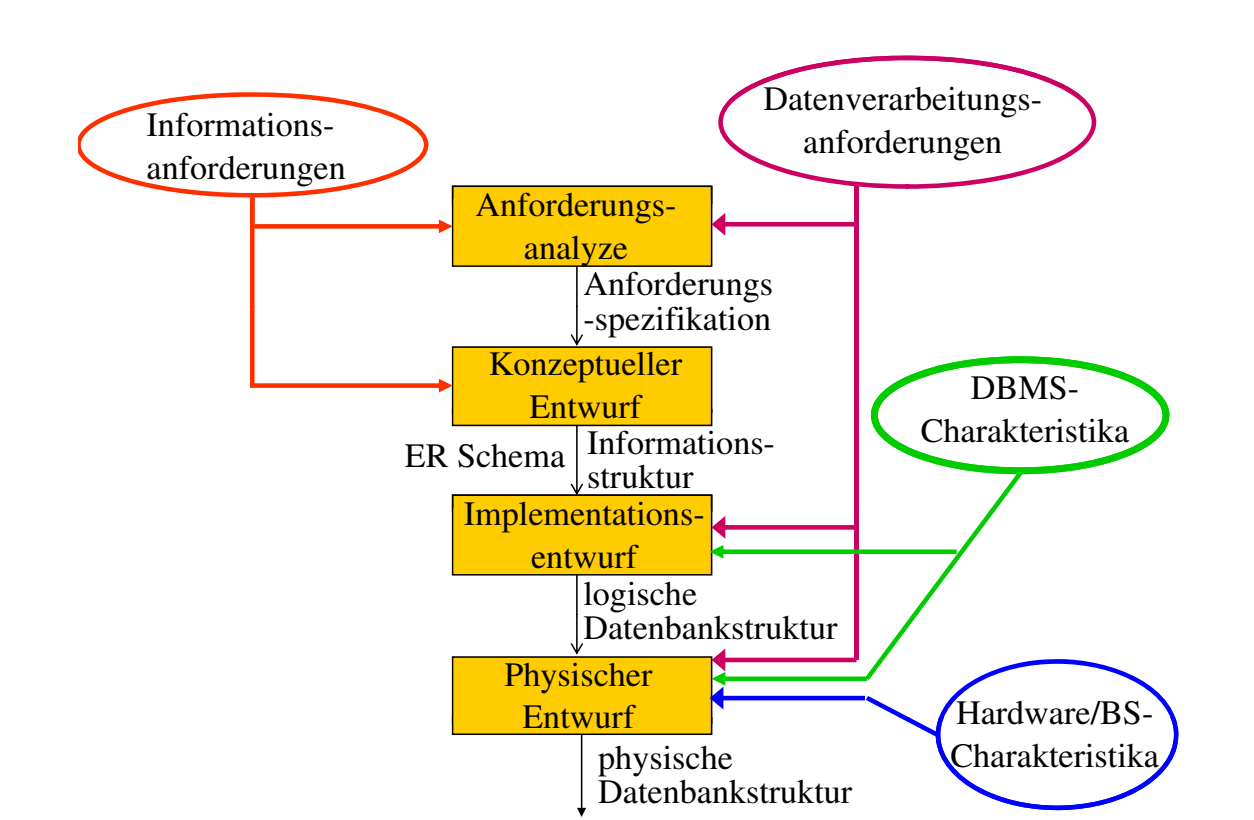
需求分析

对于对象的描述，我们可以把对象，和它对应的信息用关键词列出来

对于关系的描述，我们可以这样写，如 prüfen

对于过程的描述，如生成成绩

关系

关系有二元关系和三元关系。关系之间可以用笛卡尔积表示

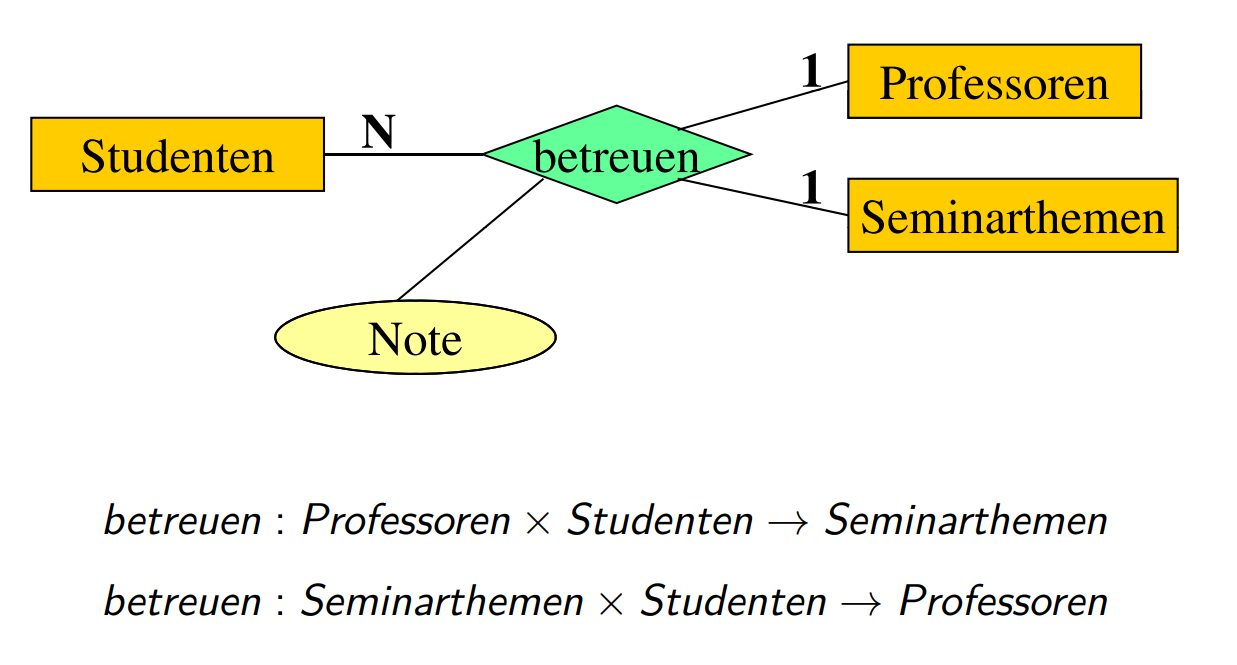
Professoren \(\times\) Studenten 就是给定他们，访问对应的 Seminarthemen

关系的数量表示

关系可以是 1对1， 1对N，和N对M...我们就把这种数量及写在上面的表上面。比如上面就是 1个教授和1个主题照顾 N 个学生。

关系也可以用最大值，最小值来明确对象的数量

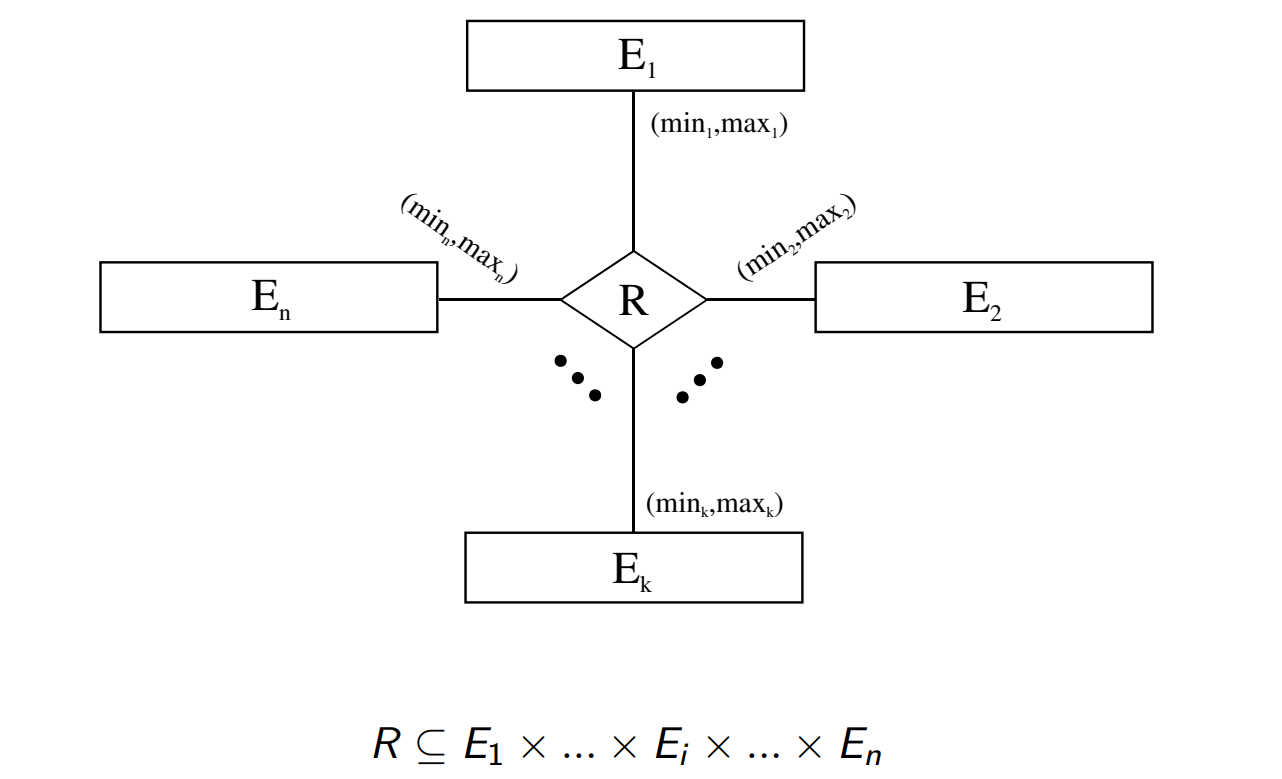
表示某个元素对应的映射 最小有多少个，最大有多少个

Schwache Entitäten

弱实体是，某个数据必须从属于另一个数据：

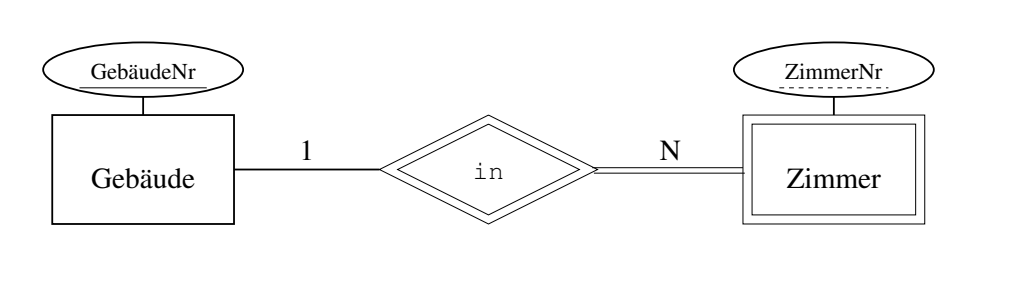
比如房间必须在建筑里面，依附于建筑存在

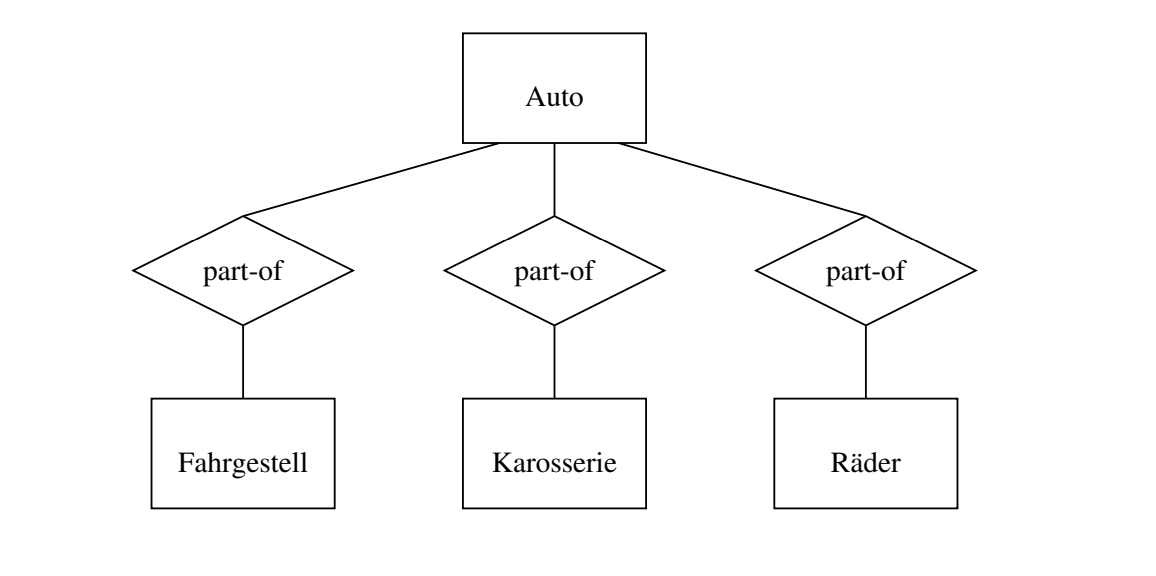
Aggregation

表示谁是谁的一部分，如轮子是车的一部分

关系代数

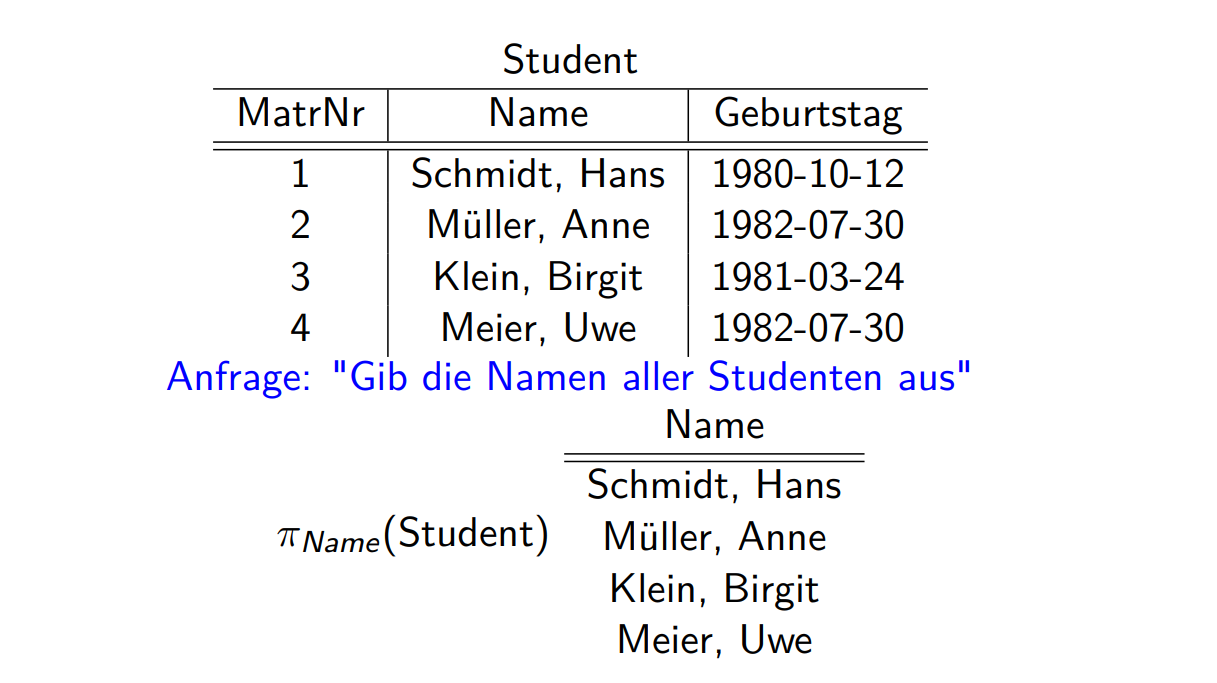
Projektion

拿出某些竖列 \[ \pi_{A_{1}, \ldots, A_{n}}(R) \]

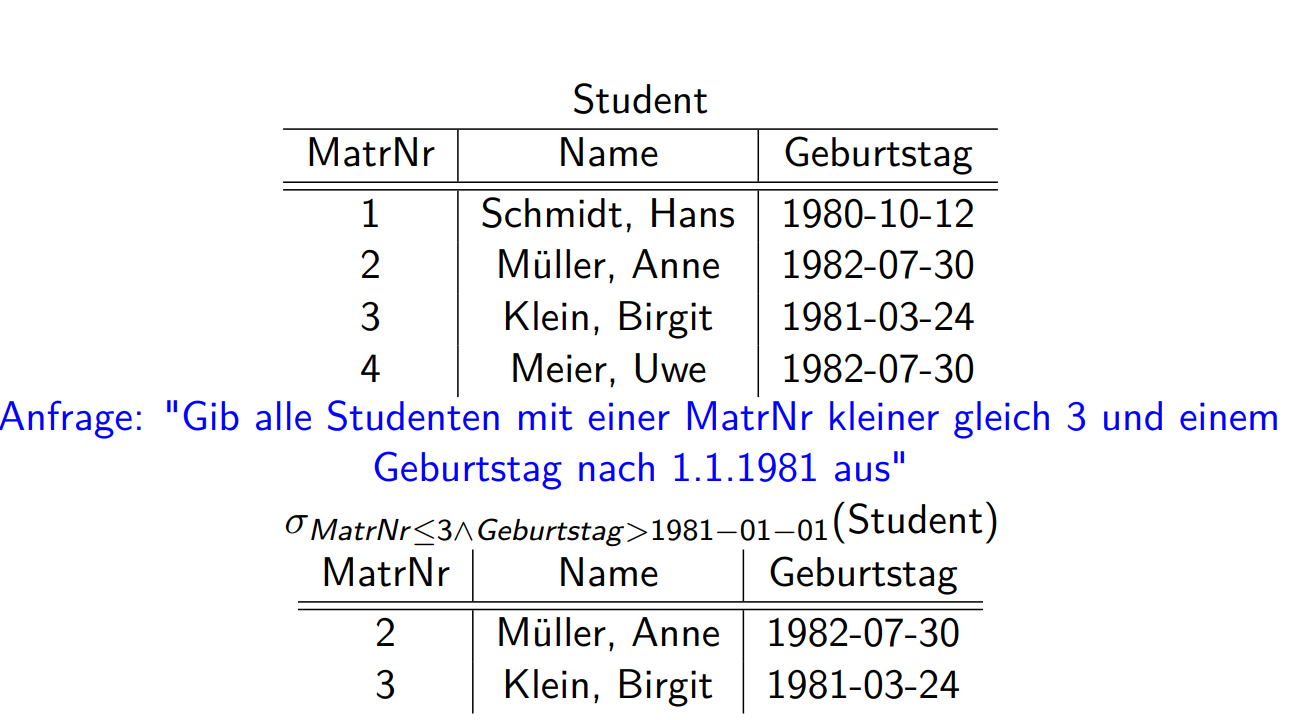
Selektion

拿出某行 \[ \sigma_{p}(R) \]

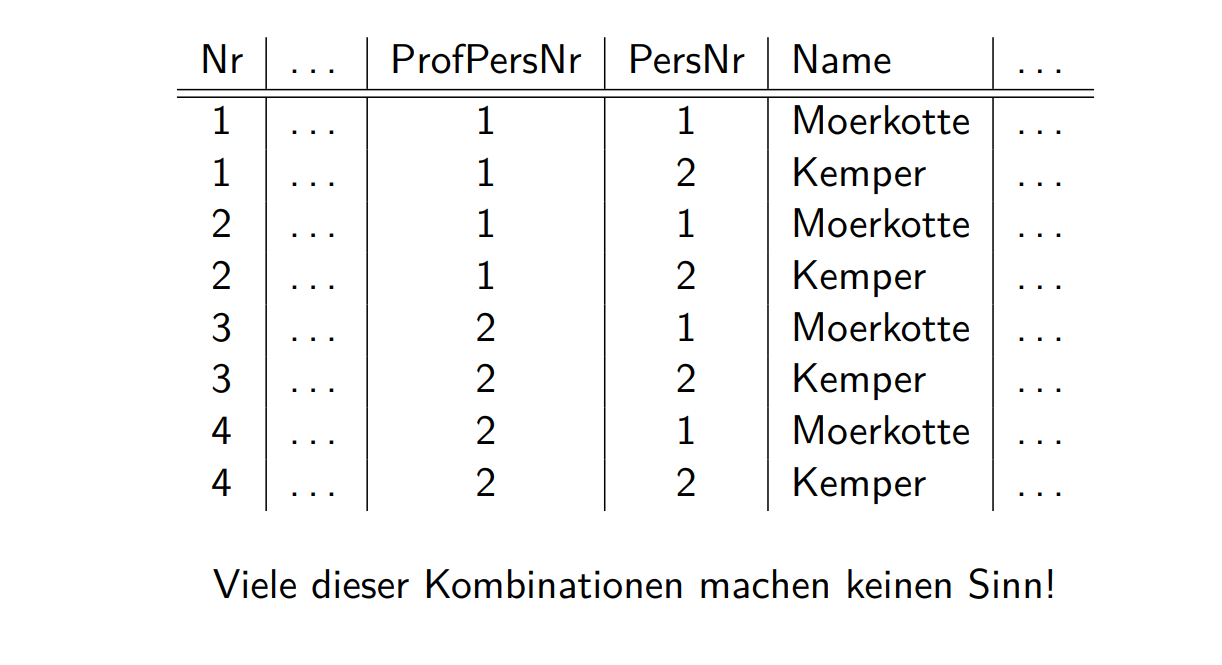
Kreuzprodukt

笛卡尔积,不常用，通常用join代替 \[ R_{1} \times R_{2} \]

Join

连接 \[ R_{1} \bowtie _{R_1 . A_{i}=R_{2} . A_{j}} R_{2}=\sigma_{R_{1} \cdot A_{i}=R_{2} \cdot A_{j}}\left(R_{1} \times R_{2}\right) \]

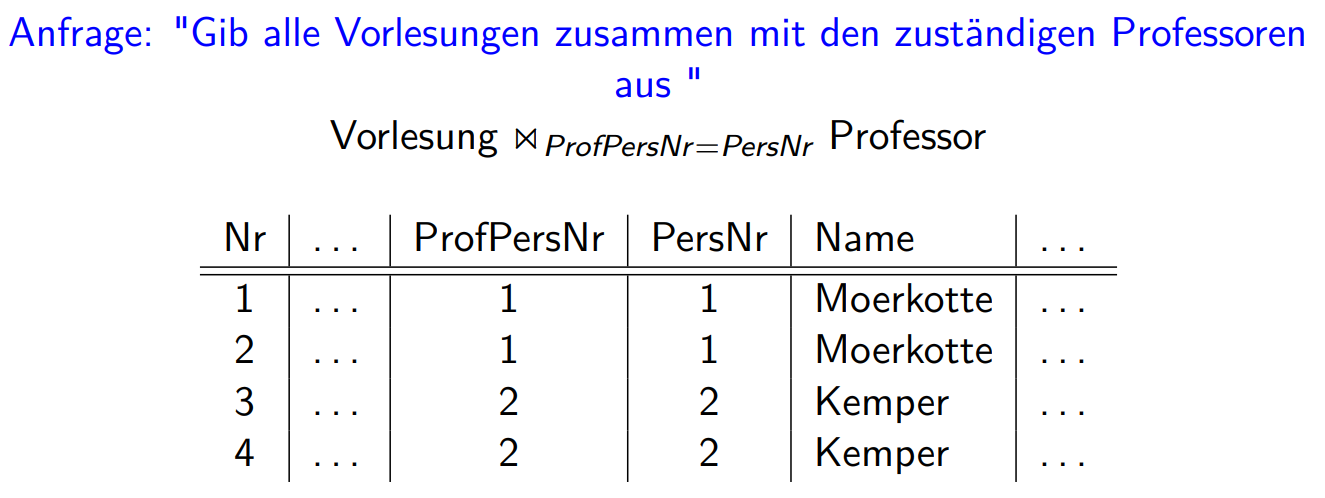
在属性相同名字不同的情况下，要另取名

Theta Join

判断可以是任何语句,如大于小于

Äußerer Join

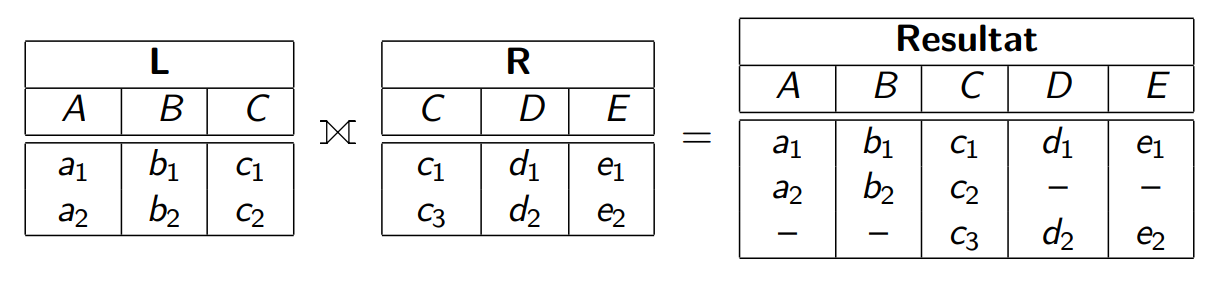
Linker Äußerer Join

Rechter Äußerer Join

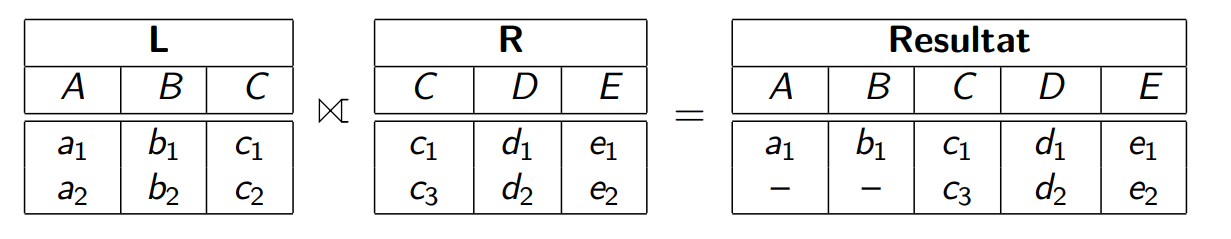
Semi-Join

只显示其中一个表格，满足情况的

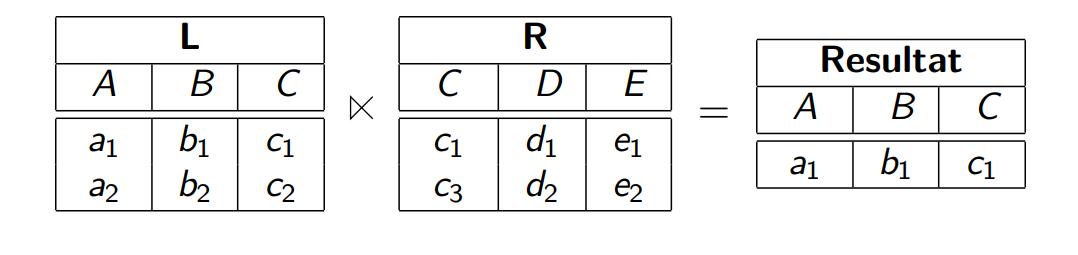
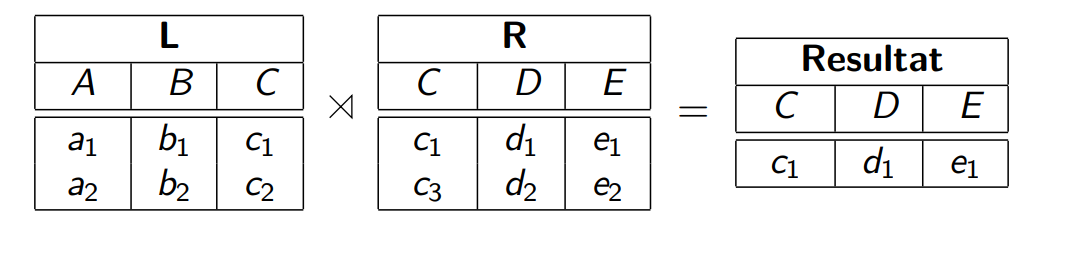
Anti-Join

只显示其中一个表格，不满足情况的

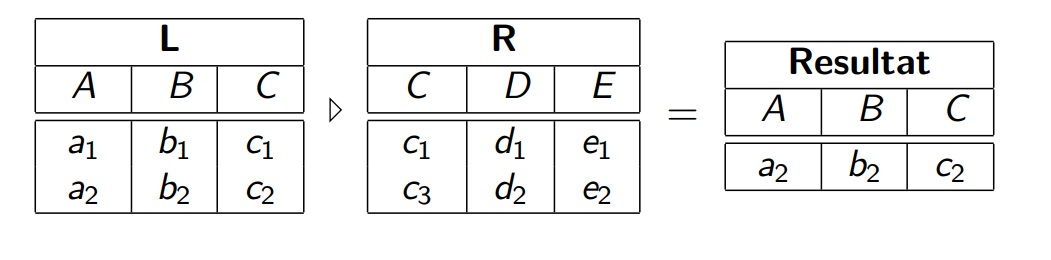
Vereinigung

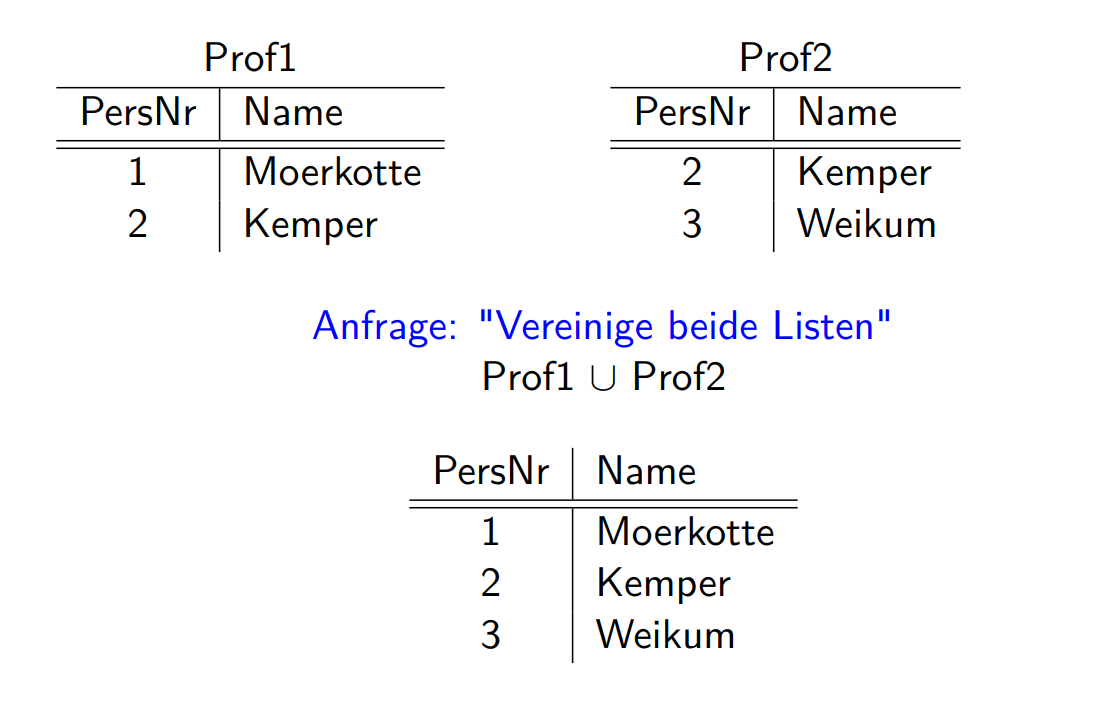
Schnitt

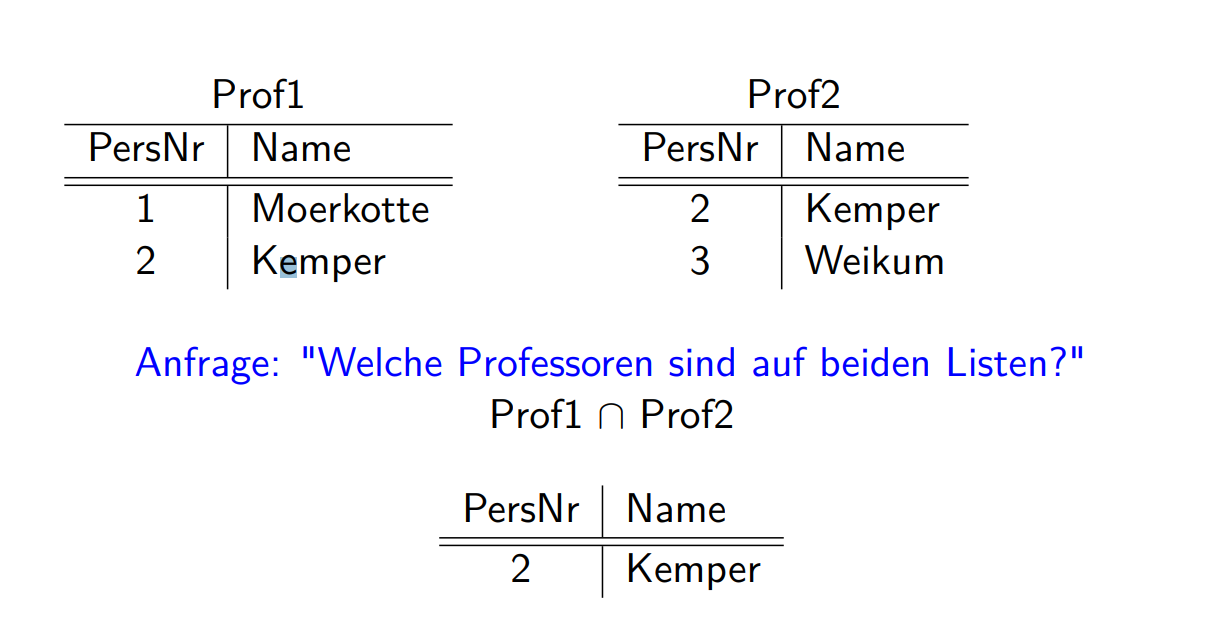
Mengendifferenz

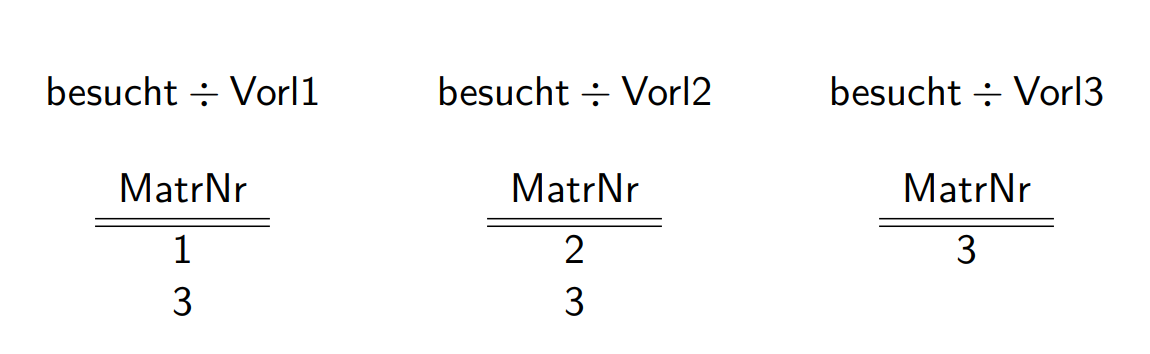
Relationale Division

哪些人听了1,2,3课 \[ R_{1} \div R_{2}=\pi_{\left(\mathcal{R}_{1} \backslash \mathcal{R}_{2}\right)}\left(R_{1}\right) \backslash \pi_{\left(\mathcal{R}_{1} \backslash \mathcal{R}_{2}\right)}\left(\left(\pi_{\left(\mathcal{R}_{1} \backslash \mathcal{R}_{2}\right)}\left(R_{1}\right) \times R_{2}\right) \backslash R_{1}\right) \]

Mengendurchschnitt

求交集，如 \[ \begin{array}{c} \Pi_{\text {PersNr }}\left(\rho_{\text {PersNr-gelesenVon }}(\text { Vorlesungen })\right) \cap \\ \quad \Pi_{\text {PersNr }}\left(\sigma_{\text {Rang }=C 4}\right. \text { (Professoren)) } \end{array} \] 只能用在相同类型的表格

关系计算 Der Relationenkalkül

一个关系计算可以用这个公式给出： \[ \{t | P(t)\} \] 比如 C4-Professoren \[ \left\{p \mid p \in \text { Professoren } \wedge \text { p.Rang }={ }^{\prime} C 4^{\prime}\right\} \] 至少听Curie一节课的学生

select s.*
from Studenten s
where exists (
     select h.*
     from hören h
     where h.MatrNr = s.MatrNr and exists (
     select *
     from Vorlesungen v
     where v.VorlNr = h.VorlNr and exists (
     select *
     from Professoren p
     where p.Name =‚Curie' and
     p.PersNr= v.gelesenVon )))

Tupelkalkül

Atome

\(s \in R\) , S 是变量， R 是关系名

数据完整性

完整条件

参照完整性

Fremdschlüssel müssen auf existierende Tupel verweisen oder einen Nullwert enthalten

静态完整条件

动态完整条件

关系型数据库开发原理

函数依赖Funtionale Abhängigkeit

\(\alpha \subseteq R, \beta \subseteq \mathcal{R}\)，\(\alpha \rightarrow \beta\) 当前仅当 \(\forall r, s \in R\) 使得 \(r . \alpha=s . \alpha \Rightarrow r . \beta=s . \beta\)

也就是唯一的 \(\alpha\) 可以确定唯一的 \(\beta\)

Schlüssel

Superschlüssel

\(\alpha \subseteq \mathcal{R}\) 是 Superschlüssel 当且仅当 \(\alpha \rightarrow \mathcal{R}\)

voll funktionale Abhängigkeit

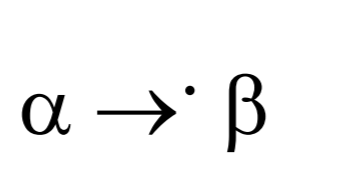
\(\alpha\) 是 \(\beta\) 的完全函数依赖，当且仅当

\(\alpha \rightarrow \beta\)
\(\alpha\) 不能简化

Kandinatenschlüssel

\(\alpha \subseteq \mathcal{R}\) 是 Kandinatenschlüssel 当且仅当 \(\alpha\) 是 \(R\) 的完全函数依赖。