第1章

定义2.1 机器数字Maschinenzahlen

有限集合 $M$ 计算机可以表示的数字

定义2.2 取整Rundung

映射 $\R \rightarrow M$ 是一个Rundung \[ |x-r d(x)|=\min _{m \in M}|x-m| \] 于是产生absolute Rundungsfehler \[ f_{r d}(x):=x-r d(x) \]

定义2.3 Festkommazahlen

\[ \begin{aligned} &n_{1} n_{2} \cdots n_{k}, m_{1} \cdots m_{j} \quad \text { mit } \\ &n_{1}, n_{2}, \ldots, n_{k}, m_{1}, \ldots, m_{j} \in\{0,1, \ldots, 9\}, \quad k, j \in I N \end{aligned} \]

补码

取反后+1
最高位符号为负数

浮点数

$x\in \R$ 可以如下表示， $m$ 是Mantisse， $e$ 是Exponenten, $b>1$ 是 Basis \[ x=(-1)^{v} \cdot m \cdot b^{e} \] 其中 $m$ 的整数部分只有1个数字

定义 2.4

\[ x=(-1)^{v} \cdot\left(\sum_{i=0}^{t-1} x_{i} 2^{-i}\right) \cdot 2^{e} \]

转化浮点数

取整规则

取整到 $t-1$ 位

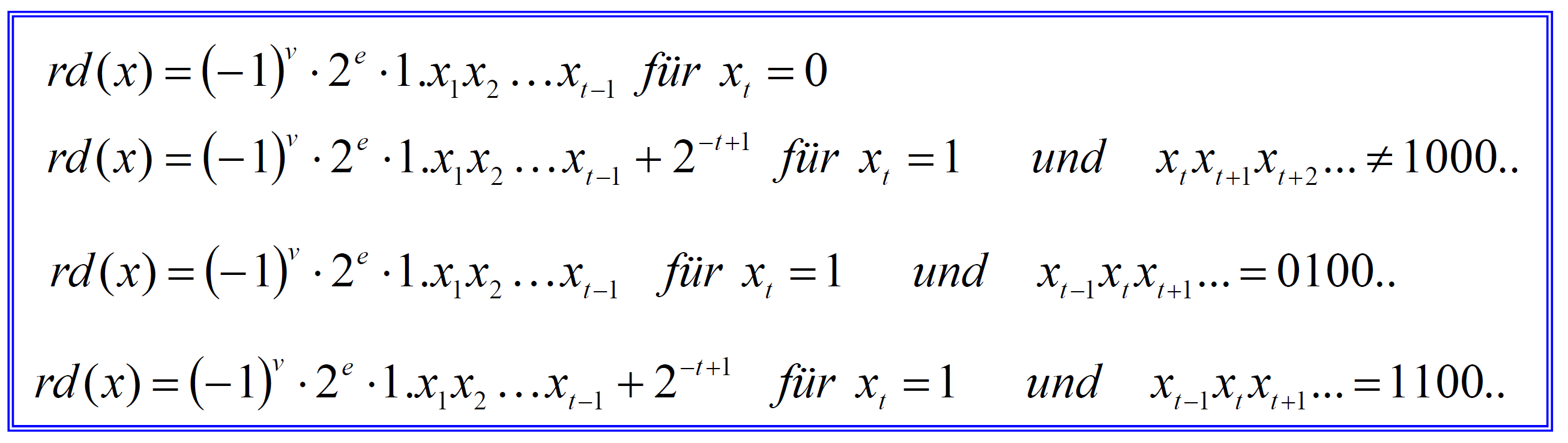
或者

Maschinengenauigkeit:

在 $t$ 位的底数浮点数计算时误差的上界

或者是最大的 $y= 2^{-k}$ 使得 \[ 1.0+y=1.0 \]

第2章

Kondition

对于函数 $y=f(x)$ 在位置 $x$ 有误差放大系数 \[ \text { cond }_{x}:=\left|\frac{x \cdot f^{\prime}(x)}{f(x)}\right| \] gut konditioniert 就是它的值=1

稳定性 Def. 2.15.: Stabilität

Sei das Problem y=f(x) gut konditioniert. Existiert dann zusätzlich auch ein gutartiges Berechnungsverfahren, bei dem die relativen Fehler nicht zusätzlich stark vergrößert werden, so spricht man von einem numerisch stabilen Algorithmus. Ein Berechnungsverfahren, das trotz kleiner Konditionszahl zu vergrößerten relativen Fehlern im Resultat führen kann, heißt numerisch instabil .

考试复习

浮点数

小数转换

整数转二进制

小数转二进制

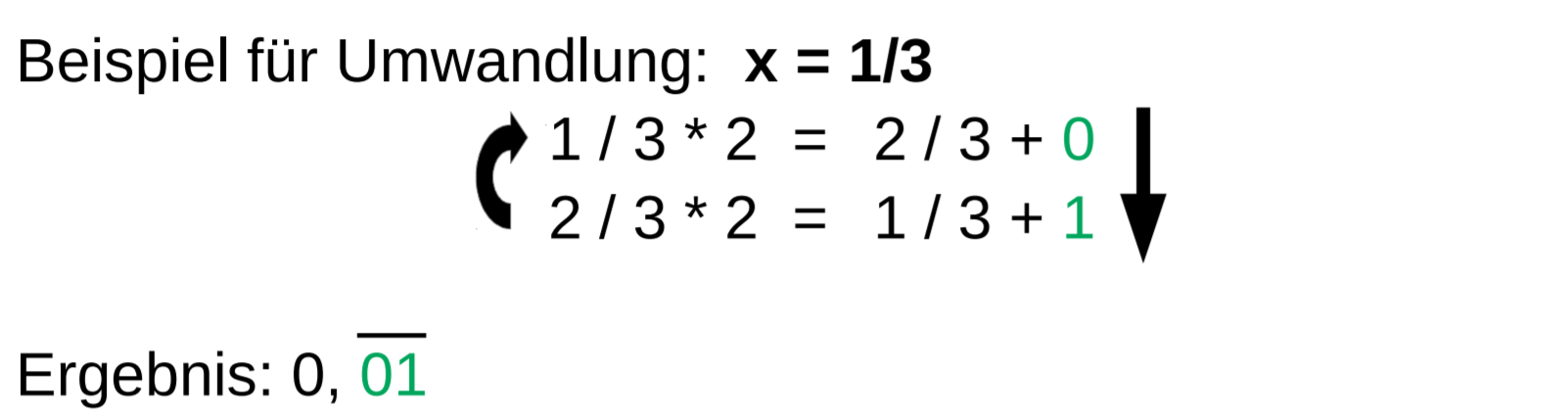
补码

浮点数

先转换成小数，如 -11/10 转换成 $-1,0\overline{0011} * 2^{0}$

然后考虑小数点后面的数字 $0\overline{0011}$ 就是mantisse,

从 $1$ 开始数第 $k$ 位 $ t_k = # (k-start) len$

$len$ 是循环位置的长度 $4$

$start$ 是循环位置开始的index 为 $2$

$\#$ 是后面那个数再循环位置($0 $ index开始)的数字 $\#0=0$

求出第 $X=t_{23},t_{24},Y=t_{25}$

然后取整

误差

$f_{abs} = |x - rd(x)|$

$f_{rel}=\frac{f_{abs}}{x}$

relative Genauigkeit der Gleitkommazahlen \[ \epsilon_{M A}=\max \left\{x \in \mathbb{R}^{+} \mid r d(1+x)=1\right\} \] 浮点数范围 \[ [1 * 2^{\exp _{\min }} , 2-2^{-m} * 2^{\exp _{\max }}] \]

Maschinengenauigkeit \[ \epsilon=\frac{1}{2} \cdot \beta^{1-t} \] $\beta$ 是basis， $t$ 是 Mantisse

IEEE:

$exp_{min}=-126$

$exp_{max}=127$

condition

\[ \operatorname{cond}(f, x)=\left|\frac{x \cdot f^{\prime}(x)}{f(x)}\right| \]

stabilität

\[ \left|\frac{\operatorname{rd}(f)(x)-f(x)}{f(x)}\right| \]

\[ \left(a \text { op }_{\mathrm{M}} b\right)=\operatorname{rd}_{\mathrm{M}}(a \text { op } b)=(a \text { op } b) \cdot\left(1+\varepsilon_{i}\right) \text { mit }\left|\varepsilon_{i}\right| \leq \varepsilon_{\mathrm{Ma}} \]

$\varepsilon_{i} \cdot \varepsilon_{j} \doteq 0 \quad \forall i, j$

Interpolation

Interpolation mit unterschiedlichen Basisfunktionen \[ \left(\begin{array}{ccc} g_{0}\left(x_{0}\right) & \cdots & g_{n}\left(x_{0}\right) \\ \vdots & & \vdots \\ g_{0}\left(x_{n}\right) & \cdots & g_{n}\left(x_{n}\right) \end{array}\right) \cdot\left(\begin{array}{c} c_{0} \\ \vdots \\ c_{n} \end{array}\right)=\left(\begin{array}{c} f\left(x_{0}\right) \\ \vdots \\ f\left(x_{n}\right) \end{array}\right) \] 带入解方程即可

Polynominterpolation nach Newton

\[ \begin{aligned} &c_{i, 0}=f\left(x_{i}\right)=y_{i} \\ &c_{i, k}=\frac{c_{i+1, k-1}-c_{i, k-1}}{x_{i+k}-x_{i}} \end{aligned} \]

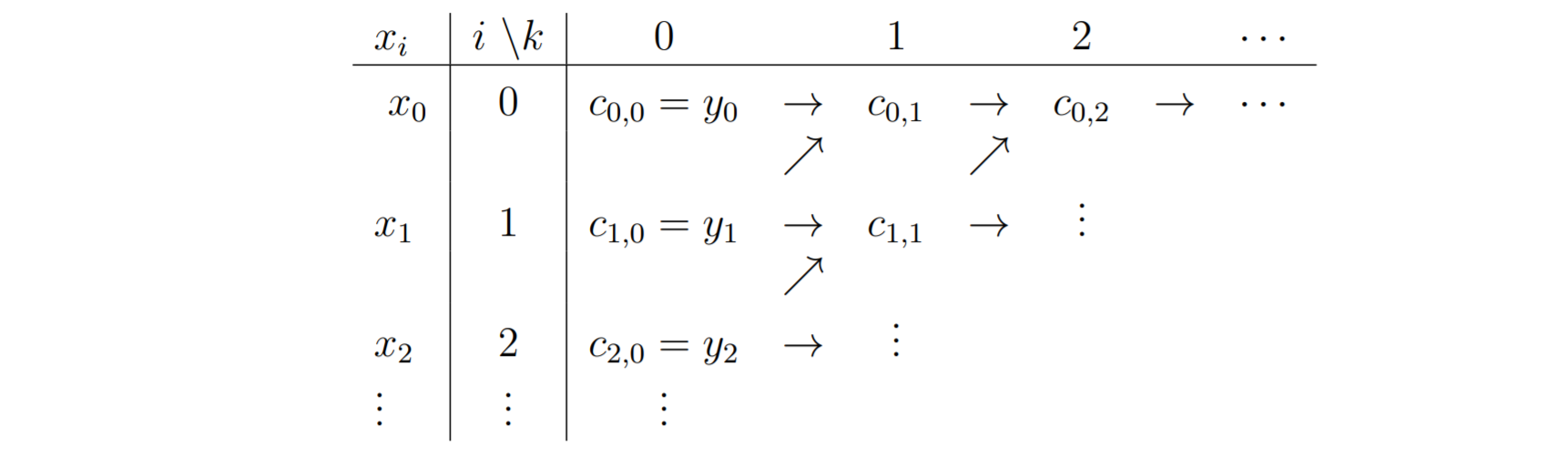\[ p(x)=c_{0,0}+c_{0,1} \cdot\left(x-x_{0}\right)+\ldots+c_{0, n} \cdot \prod_{i=0}^{n-1}\left(x-x_{i}\right) \]

Polynominterpolation mit Aitken-Neville

\[ p[i, k]:=p[i, k-1]+\frac{x-x[i]}{x[i+k]-x[i]} \cdot(p[i+1, k-1]-p[i, k-1]) \]

Stückweise Hermite-Interpolation

\[ p\left(x_{0}\right)=y_{0}, \quad p\left(x_{1}\right)=y_{1}, \quad p^{\prime}\left(x_{0}\right)=y_{0}^{\prime}, \quad p^{\prime}\left(x_{1}\right)=y_{1}^{\prime} \]

根据这个条件列方程 \[ p(t)=a_{0}+a_{1} t+a_{2} t^{2}+a_{3} t^{3}, \quad t \in[0 ; 1]=\left[x_{0} ; x_{1}\right] \]

\[ p^{\prime}(t)=a_{1}+2 a_{2} t+3 a_{3} t^{2}, \quad t \in[0 ; 1]=\left[x_{0} ; x_{1}\right] \]

解出来就可以了

下面是基函数，用于区间映射 \[ \begin{aligned} H_{0}(t) &=1-3 t^{2}+2 t^{3} \\ H_{1}(t) &=3 t^{2}-2 t^{3} \\ H_{2}(t) &=t-2 t^{2}+t^{3} \\ H_{3}(t) &=-t^{2}+t^{3} \end{aligned} \]

\[ t_{i}(x):=\frac{x-x_{i}}{x_{i+1}-x_{i}}=\frac{x-x_{i}}{h_{i}} \in[0 ; 1] \]

\[ p_{i}\left(t_{i}(x)\right)=y_{i} \cdot H_{0}\left(t_{i}(x)\right)+y_{i+1} \cdot H_{1}\left(t_{i}(x)\right)+h_{i} \cdot y_{i}^{\prime} \cdot H_{2}\left(t_{i}(x)\right)+h_{i} \cdot y_{i+1}^{\prime} \cdot H_{3}\left(t_{i}(x)\right) \]

Interpolation mit kubischen Splines

\[ x_{i+1}-x_{i}=h:=\frac{x_{n}-x_{0}}{n} ; \quad i=0,1, \ldots, n-1 \]

\[ \left[\begin{array}{cccc} 4 & 1 & & \\ 1 & 4 & \ddots & \\ & \ddots & \ddots & 1 \\ & & 1 & 4 \end{array}\right] \cdot\left(\begin{array}{c} y_{1}^{\prime} \\ y_{2}^{\prime} \\ \vdots \\ y_{n-2}^{\prime} \\ y_{n-1}^{\prime} \end{array}\right)=\frac{3}{h} \cdot\left(\begin{array}{c} y_{2}-y_{0} \\ y_{3}-y_{1} \\ \vdots \\ y_{n-1}-y_{n-3} \\ y_{n}-y_{n-2} \end{array}\right)-\left(\begin{array}{c} y_{0}^{\prime} \\ 0 \\ \vdots \\ 0 \\ y_{n}^{\prime} \end{array}\right) \]

FFT

\[ c_{k}=(\operatorname{DFT}(v))_{k}:=\frac{1}{n} \sum_{j=0}^{n-1} v_{j} \cdot \bar{\omega}^{j k} \quad k=0,1, \ldots, n-1 \]

\[ v_{l}=(\operatorname{IDFT}(c))_{l}:=\sum_{k=0}^{n-1} c_{k} \cdot \omega^{k l} \quad l=0,1, \ldots, n-1 \]

\[ \begin{aligned} \omega &=\exp \left(i \cdot \frac{2 \pi}{n}\right) \\ &=\cos \left(\frac{2 \pi}{n}\right)+i \cdot \sin \left(\frac{2 \pi}{n}\right) \\ \bar{\omega} &=\cos \left(\frac{2 \pi}{n}\right)-i \cdot \sin \left(\frac{2 \pi}{n}\right)=\omega^{-1} \end{aligned} \]

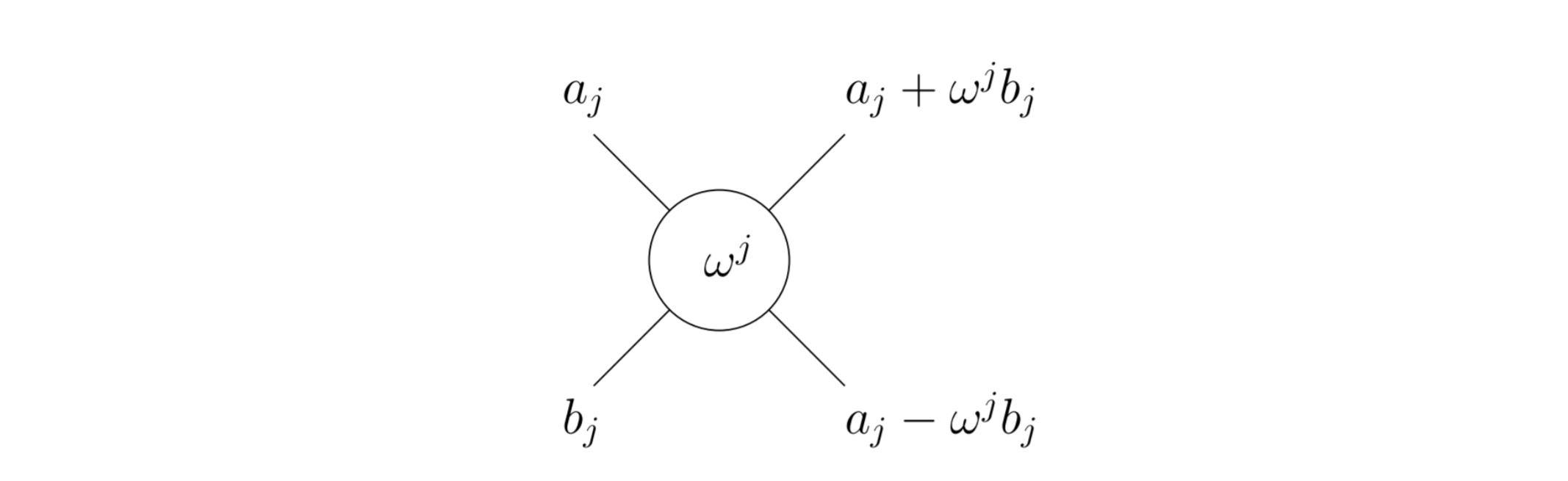
交织在一起的操作 j+1, j 从 0 开始

积分

拉格朗日

\[ \int_{a}^{b} f(x) \mathrm{d} x \approx \int_{a}^{b} p(x) \mathrm{d} x=\int_{a}^{b} \sum_{i=1}^{n} f\left(x_{i}\right) \cdot L_{i}(x) \mathrm{d} x \]

\[ L_{j}=\prod_{i=0 ; i \neq j}^{n-1} \frac{x-x_{i}}{x_{j}-x_{i}} \]

Trapezregel und Trapezsumme

\[ \begin{aligned} Q_{\mathrm{T}}(f) &=H \cdot \frac{f(a)+f(b)}{2} \\ Q_{\mathrm{TS}}(f ; h) &=h \cdot\left(\frac{f_{0}}{2}+f_{1}+\ldots+f_{n-1}+\frac{f_{n}}{2}\right) \end{aligned} \]

\[ R_{\mathrm{TS}}(f ; h)=h^{2} \cdot H \cdot \frac{f^{(2)}(\xi)}{12} \text { mit } \xi \in[a, b] \]

Keplersche Fassregel und Simpson-Summe

\[ \begin{aligned} Q_{\mathrm{F}}(g) &=H \cdot \frac{g(a)+4 g\left(\frac{a+b}{2}\right)+g(b)}{6} \\ Q_{\mathrm{SS}}(g ; h) &=\frac{h}{3} \cdot\left(g_{0}+4 g_{1}+2 g_{2}+4 g_{3}+\ldots+2 g_{n-2}+4 g_{n-1}+g_{n}\right), \end{aligned} \]

\[ R_{\mathrm{SS}}(g ; h)=h^{4} \cdot H \cdot \frac{g^{(4)}(\xi)}{180} \text { mit } \xi \in[a, b] \]

Quadratur nach Romberg

\[ Q_{i, k}=Q_{i, k-1}+\frac{Q_{i, k-1}-Q_{i-1, k-1}}{\frac{h_{i-k}^{2}}{h_{i}^{2}}-1} \quad, 1 \leq i \leq k \]

\[ Q_{\mathrm{TS}}(f ; h)=\frac{Q_{\mathrm{TS}}(f ; 2 h)}{2}+h \cdot\left(f_{1}+f_{3}+\ldots+f_{N-3}+f_{N-1}\right) \]

Gauß Quadratur

\[ \sum_{i=0}^{n-1} f_{k}\left(x_{i}\right) \cdot w_{i} \stackrel{!}{=} \int_{a}^{b} f_{k}(x) \]

$n$ Stützstellen plus $n$ Gewichte ergibt $2n$ Freiheitsgrad

ein LGS mit $2n$ Gleichungen. Das ergibt Polynom von Grad $2n-1$

Die Gaußquadratur passt dynamisch die Stützstellen an. Wenn man also die Anzahl dieser verändert,

ändern sich deren Positionen. Damit muss man also doppelt soviele Funktionsauswertungen machen

im Vergleich zur Trepezsumme, da wir dort die der vorherigen wiederverwenden können.

Fixpunkte

Newton Verfahren

\[ x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)} \]

ODE

Explizites Euler-Verfahren:

\[ \begin{aligned} t_{k} &=t_{0}+k \cdot \delta t \\ y_{k+1} &=y_{k}+\delta t \cdot f\left(t_{k}, y_{k}\right) \end{aligned} \]

Verfahren von Heun:

\[ \begin{aligned} t_{k} &=t_{0}+k \cdot \delta t \\ y_{k+1} &=y_{k}+\frac{\delta t}{2} \cdot\left(f\left(t_{k}, y_{k}\right)+f\left(t_{k+1}, y_{k}+\delta t \cdot f\left(t_{k}, y_{k}\right)\right)\right) \end{aligned} \]

Klassisches Runge-Kutta-Verfahren

\[ \begin{aligned} t_{k} &=t_{0}+k \cdot \delta t \\ T_{1} &=f\left(t_{k}, y_{k}\right) \\ T_{2} &=f\left(t_{k}+\frac{\delta t}{2}, y_{k}+\frac{\delta t}{2} T_{1}\right) \\ T_{3} &=f\left(t_{k}+\frac{\delta t}{2}, y_{k}+\frac{\delta t}{2} T_{2}\right) \\ T_{4} &=f\left(t_{k+1}, y_{k}+\delta t T_{3}\right) \\ y_{k+1} &=y_{k}+\frac{\delta t}{6} \cdot\left(T_{1}+2 T_{2}+2 T_{3}+T_{4}\right) \end{aligned} \]

Implizites Euler-Verfahren

\[ y_{k+1}=y_{k}+h f\left(t_{k+1}, y_{k+1}\right) \]

Das bedeutet zum Beispiel auch, dass wenn man die Schrittweite bei einem Verfahren zweiter Ordnung halbieren würde, sich der Fehler vierteln würde.

解方程

高斯消元

找pivot 找绝对值最大的那个

Jacobi Verfahren

\[ x^{(k+1)}=x^{(k)}+\operatorname{diag}(A)^{-1}\left(b-A x^{(k)}\right) \]

\[ \begin{aligned} r^{(k)} &=b-A x^{(k)} \\ y_{i}^{(k)} &=\frac{1}{a_{i i}} \cdot r_{i}^{(k)} \quad \forall i \in[1, \ldots, n] \\ x^{(k+1)} &=y^{(k)}+x^{(k)} \end{aligned} \]

Gauß-Seidel Verfahren

\[ r_{i}^{(k)}=b_{i}-\sum_{m=1}^{i-1} a_{i m} x_{m}^{(k+1)}-\sum_{m=i}^{n} a_{i m} x_{m}^{(k)} \quad \forall i=1, \ldots, n \]

\[ \begin{aligned} r_{i}^{(k)} &=b_{i}-\sum_{m=1}^{i-1} a_{i m} x_{m}^{(k+1)}-\sum_{m=i}^{n} a_{i m} x_{m}^{(k)} \\ y_{i}^{(k)} &=\frac{1}{a_{i i}} \cdot r_{i}^{(k)} \\ x_{i}^{(k+1)} &=y_{i}^{(k)}+x_{i}^{(k)} \end{aligned} \]

Gauss vs Jacobi:

Gauss hat weniger Speicheraufwand und bessere Konvergenzgeschwindigkeit.

Verfahren des steilsten Abstiegs

\[ r^{(i)}=b-A x^{(i)} \]

\[ \alpha^{(i)}=\frac{r^{(i)^{T}} r^{(i)}}{r^{(i)^{T}} A r^{(i)}} \]

\[ x^{(i+1)}=x^{(i)}+\alpha^{(i)} r^{(i)} \]

Eigenvalue

求 eigenvalue \[ det(A-\lambda I)=0 \] eigenvector \[ (A-\lambda_i I)v_i=0 \] condition for matrix \[ \kappa(A)=\left|\frac{\lambda_{\max }(A)}{\lambda_{\min }(A)}\right| \]