建模和仿真
Focus Analysis
基础部分
多变量函数
定义
\[ f: D \rightarrow W, D \subseteq \mathbb{R}^{n}, W \subseteq \mathbb{R}^{m} \]
对于自然数 \(n\) 和 \(m\)
这个函数可以这样表示: \[ f: D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}, x=\left(\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right) \mapsto f(x)=\left(\begin{array}{c} f_{1}\left(x_{1}, \ldots, x_{n}\right) \\ \vdots \\ f_{m}\left(x_{1}, \ldots, x_{n}\right) \end{array}\right) \]
高维度拓扑学
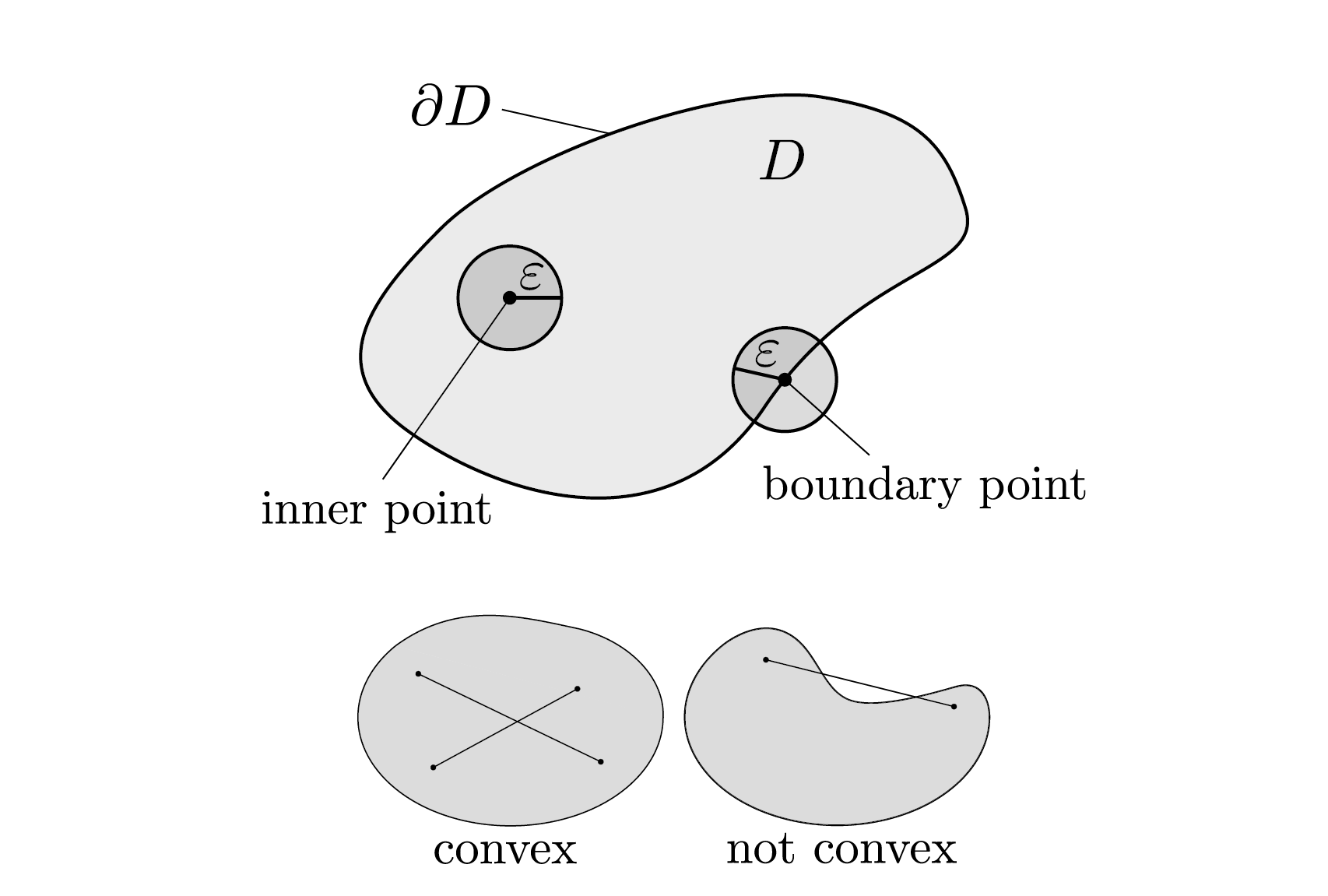
定义域Domain \(D\subseteq \R ^n\) 定义补集complement 为 \(D^c=\R^n \setminus D\) ,欧几里得模Euclidean norm为 \[ \left\|\left(x_{1}, \ldots, x_{n}\right)^{\top}\right\|=\sqrt{x_{1}^{2}+\cdots+x_{n}^{2}} \] 一个点 \[\boldsymbol{x}_{0} \in D\]是内部点 inner point 若存在 \(\varepsilon > 0\) 使得 \(\varepsilon\)-ball \[ B_{\varepsilon}\left(\boldsymbol{x}_{0}\right)=\left\{\boldsymbol{x} \in \mathbb{R}^{n} \mid\left\|\boldsymbol{x}-\boldsymbol{x}_{0}\right\|<\varepsilon\right\} \subseteq D \] 也就是存在一个周围的小球,它也在\(D\) 里面
所有内部点的集合写作 \(\stackrel{\circ}{D}\)
一个 Domain \(D\) 是开的open 若 \(D=\stackrel{\circ}{D}\)
一个点是边界点 boundary point 若对于任意 \(\varepsilon > 0\) 有 \[ B_{\varepsilon}\left(\boldsymbol{x}_{0}\right) \cap D \neq \emptyset \] 且 \[ B_{\varepsilon}\left(\boldsymbol{x}_{0}\right) \cap D^{c} \neq \emptyset \] 所有边界点的集合叫做 \(D\) 的边界 boundary, 写作 \(\partial D\)
- 集合\(\bar{D}=D \cup \partial D\) 是 \(D\) 的closure闭包
- 定义域是 closed 若\(\partial D \subseteq D\)
- 定义域是 bounded 若 \(\exists K \in \mathbb{R}:\|\boldsymbol{x}\|<K, \forall \boldsymbol{x} \in D\)
- 定义域是 compact 若同时 closed 且 bounded
- 定义域是 convex 若对于所有 \(0\le \alpha \le 1\) 有
\[ \forall \boldsymbol{x}, \boldsymbol{y} \in D: \alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y} \in D, \]
连续性
考虑向量数列\(\left(\boldsymbol{x}^{(k)}\right)_{k \in \mathbb{N}_{0}}\) \[ \boldsymbol{x}^{(k)}=\left(x_{1}^{(k)}, \ldots, x_{n}^{(k)}\right)^{\top} \in \mathbb{R}^{n} \] 我们说它收敛converges to于极限 \(\boldsymbol{x}\) 若 \[ \lim _{k \rightarrow \infty}\left\|\boldsymbol{x}^{(k)}-\boldsymbol{x}\right\|=0 \] 也可以写成
\(\boldsymbol{x}^{(k)} \stackrel{k \rightarrow \infty}{\longrightarrow} \boldsymbol{x}\) 或者 \(\boldsymbol{x}^{(k)} \rightarrow \boldsymbol{x}\) 或者 \[\lim _{k \rightarrow \infty} \boldsymbol{x}^{(k)}=\boldsymbol{x}\]
也即是向量中的每一个元素收敛于各自对对应的元素 \[ \boldsymbol{x}^{(k)}=\left(\begin{array}{c} x_{1}^{k} \\ \vdots \\ x_{n}^{(k)} \end{array}\right) \rightarrow \boldsymbol{x}=\left(\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right) \Leftrightarrow x_{1}^{(k)} \rightarrow x_{1}, \ldots, x_{n}^{(k)} \rightarrow x_{n} \] \(f\) 在 \(\boldsymbol{a}\in D\) 连续,若对于所有收敛于\(\boldsymbol{a}\) 的序列 \(\left(\boldsymbol{x}^{(k)}\right)_{k \in \mathbb{N}_{0}}\)
都满足 \(\left(f\left(\boldsymbol{x}^{(k)}\right)\right)_{k \in \mathbb{N}_{0}}\) 收敛于 \(f(\boldsymbol{a})\)
偏导数
下面我们考虑在标量空间下的偏导数
对于函数: \[ f: D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}, \boldsymbol{x}=\left(x_{1}, \ldots, x_{n}\right)^{\top} \mapsto f(\boldsymbol{x})=f\left(x_{1}, \ldots, x_{n}\right) \] 对于每个单位向量 \(\boldsymbol{v}\) 和点 \(\boldsymbol{a} \in D\) 我们可以计算方向导数 directional derivative \[ \frac{\partial f}{\partial \boldsymbol{v}}(\boldsymbol{a})=\partial_{\boldsymbol{v}} f(\boldsymbol{a})=f_{\boldsymbol{v}}(\boldsymbol{a})=\lim _{h \rightarrow 0} \frac{f(\boldsymbol{a}+h \boldsymbol{v})-f(\boldsymbol{a})}{h} \] (若极限存在)
然后我们可以定义 \(f\) 在 \(\boldsymbol{a}\) 上的偏导数 partial derivatives 关于 \(x_i\) \[ \frac{\partial f}{\partial x_{i}}(\boldsymbol{a})=\partial_{i} f(\boldsymbol{a})=f_{x_{i}}(\boldsymbol{a})=\lim _{h \rightarrow 0} \frac{f\left(\boldsymbol{a}+h \boldsymbol{e}_{i}\right)-f(\boldsymbol{a})}{h}, i \in\{1, \ldots, n\} \] 如果所有 \(n\) 个偏导数都存在,我们说 \(f\) 在 \(\boldsymbol{a}\) 上是可偏微分的,并且定义\(f\) 在 \(\boldsymbol{a}\) 上的梯度 gradient \[ \nabla f(\boldsymbol{a})=\left(\begin{array}{c} f_{x_{1}}(\boldsymbol{a}) \\ \vdots \\ f_{x_{n}}(\boldsymbol{a}) \end{array}\right) \] 另一种写法是 \[ \nabla f(\boldsymbol{a})=\operatorname{grad} f(\boldsymbol{a}) \] 若 \(f_{x_1}...f_{x_n}\) 都连续,那么可以定义每个单位向量 \(\boldsymbol{v}, \| \boldsymbol{v} \|=1\) 和 \(\boldsymbol{a} \in D\) \[ \frac{\partial f}{\partial \boldsymbol{v}}(\boldsymbol{a})=\langle\nabla f(\boldsymbol{a}), \boldsymbol{v}\rangle \]
黑塞矩阵
若偏导数 \(f_1,...f_n\) 连续且可偏导我们可以定义二阶偏导数second order partial derivatives 为 \[ \partial_{x_{j}} \partial_{x_{i}} f(\boldsymbol{x})=\frac{\partial^{2} f}{\partial x_{j} \partial x_{i}}(\boldsymbol{x})=\partial_{j} \partial_{i} f(\boldsymbol{x})=f_{x_{j} x_{i}}(\boldsymbol{x}) \] 我们可以定义 \(C^k(D)\) 是所有 \(k\) 次可偏导的函数的集合
对于 \(f: D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}\) 这个 \(n\times n\) 的矩阵 \[ H_{f}(\boldsymbol{x})=\left(\begin{array}{ccc} f_{x_{1} x_{1}}(\boldsymbol{x}) & \ldots & f_{x_{1} x_{n}}(\boldsymbol{x}) \\ \vdots & & \vdots \\ f_{x_{n} x_{1}}(\boldsymbol{x}) & \ldots & f_{x_{n} x_{n}}(\boldsymbol{x}) \end{array}\right) \] 是\(f\) 在 \(\boldsymbol{x}\) 上的黑塞矩阵 ,若 \(f \in C^2(D)\) 那么这个矩阵是对称的
雅可比矩阵
接下来我们考虑在向量空间上的偏导数
若 \(f: D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) 在 \(D\) 上可偏导,也就是所有 \(mn\) 个偏导数 \(\frac{\partial f_{i}}{\partial x_{j}}, 1 \leq i \leq m, 1 \leq j \leq n\) 存在,可以定义雅可比矩阵 Jacobian matrix \[ D f(\boldsymbol{x})=\left(\frac{\partial f_{i}}{\partial x_{j}}(\boldsymbol{x})\right)_{i j}=\left(\begin{array}{ccc} \frac{\partial f_{1}}{\partial x_{1}}(\boldsymbol{x}) & \ldots & \frac{\partial f_{1}}{\partial x_{n}}(\boldsymbol{x}) \\ \vdots & & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\boldsymbol{x}) & \ldots & \frac{\partial f_{m}}{\partial x_{n}}(\boldsymbol{x}) \end{array}\right)=\left(\begin{array}{c} \nabla f_{1}(\boldsymbol{x})^{\top} \\ \vdots \\ \nabla f_{m}(\boldsymbol{x})^{\top} \end{array}\right) \] 也可以写作\(D f(\boldsymbol{x})=\nabla f(\boldsymbol{x})^{\top}\) , \(J_{f}(\boldsymbol{x})\)
雅可比矩阵的计算公式
\[ D(f+g)(\boldsymbol{x})=D f(\boldsymbol{x})+D g(\boldsymbol{x}) \]
\[ D(\lambda f)(\boldsymbol{x})=\lambda D f(\boldsymbol{x}) \text { for all } \lambda \in \mathbb{R} \]
\[ D\left(f^{\top} g\right)(\boldsymbol{x})=f(\boldsymbol{x})^{\top} D g(\boldsymbol{x})+g(\boldsymbol{x})^{\top} D f(\boldsymbol{x}) \]
\[ D(f \circ g)(\boldsymbol{x})=D f(g(\boldsymbol{x})) D g(\boldsymbol{x}) \]
微分运算符
对于标量函数\(f: D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}\) 可以定义
拉普拉斯运算符 The Laplace operator
\[ \Delta f=\sum_{i=1}^{n} \partial_{i}^{2} f=\partial_{1}^{2} f+\cdots+\partial_{n}^{2} \]
The divergence:
对于向量函数 \[ \operatorname{div} \boldsymbol{v}=\nabla \cdot \boldsymbol{v}=\sum_{i=1}^{n} \partial_{i} v_{i}=\partial_{1} v_{1}+\cdots+\partial_{n} v_{n} \]
旋转
对于三维向量: \[ \operatorname{rot} \boldsymbol{v}=\left(\begin{array}{l} \partial_{2} v_{3}-\partial_{3} v_{2} \\ \partial_{3} v_{1}-\partial_{1} v_{3} \\ \partial_{1} v_{2}-\partial_{2} v_{1} \end{array}\right) \]
泰勒展开式
给定一个二阶可偏导的标量函数\(f: D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}\) 可以定义泰勒多项式 \[ T_{0, f, a}(\boldsymbol{x})=f(\boldsymbol{a}) \]
\[ T_{1, f, a}(\boldsymbol{x})=f(\boldsymbol{a})+\nabla f(\boldsymbol{a})^{\top}(\boldsymbol{x}-\boldsymbol{a}) \]
\[ T_{2, f, a}(\boldsymbol{x})=f(\boldsymbol{a})+\nabla f(\boldsymbol{a})^{\top}(\boldsymbol{x}-\boldsymbol{a})+\frac{1}{2}(\boldsymbol{x}-\boldsymbol{a})^{\top} H_{f}(\boldsymbol{a})(\boldsymbol{x}-\boldsymbol{a}) \]
坐标变换
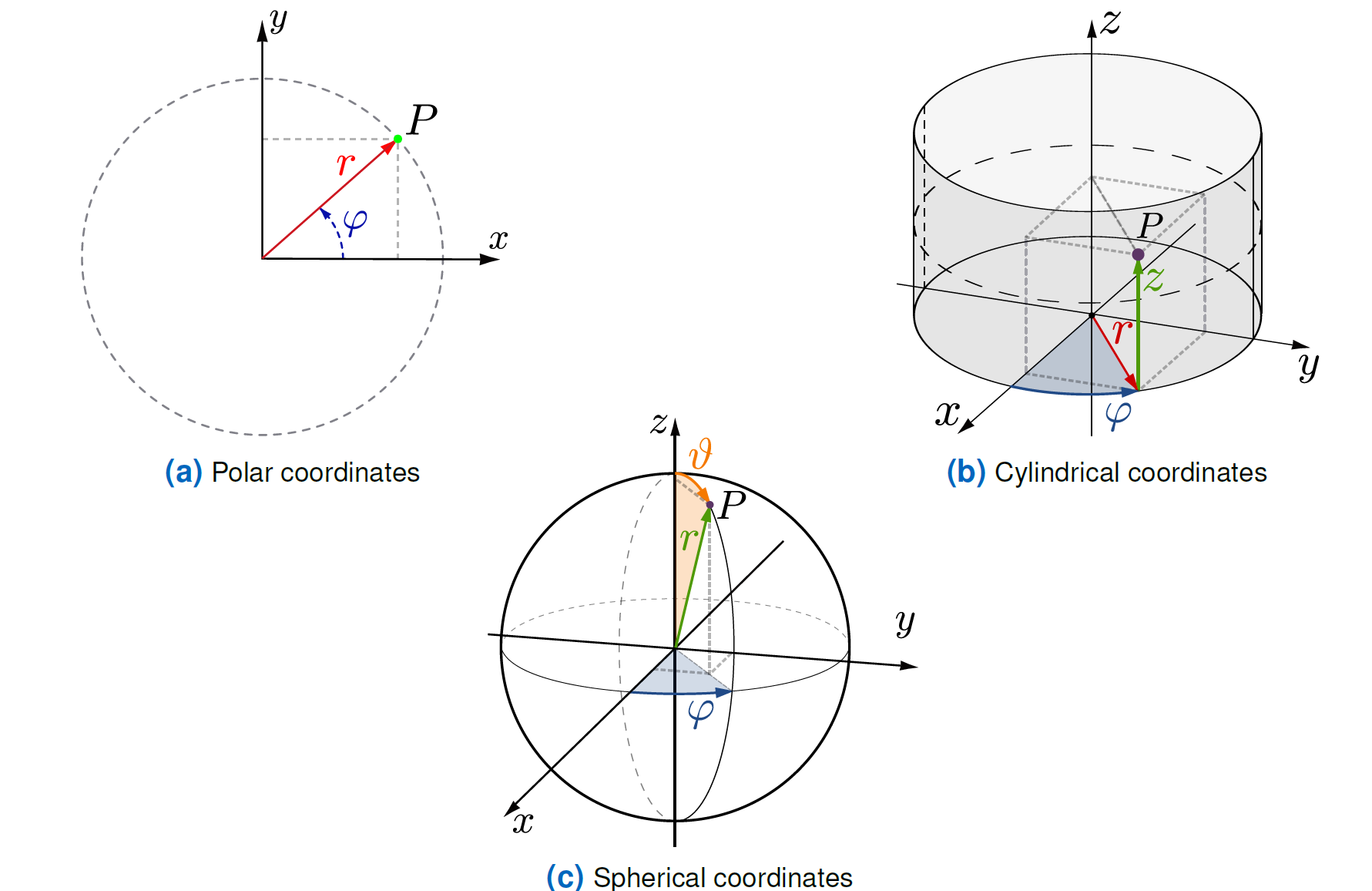
极坐标
\[ \phi:\left\{\begin{aligned} \mathbb{R}_{>0} \times[0,2 \pi[& \rightarrow & \mathbb{R}^{2} \backslash\{0\} \\ \left(\begin{array}{c} r \\ \varphi \end{array}\right) & \mapsto\left(\begin{array}{l} x \\ y \end{array}\right)=\left(\begin{array}{c} r \cos \varphi \\ r \sin \varphi \end{array}\right) \end{aligned}\right. \]
是一个坐标变换 \[ D \phi(r, \varphi)=\left(\begin{array}{cc} \cos \varphi & -r \sin \varphi \\ \sin \varphi & r \cos \varphi \end{array}\right) \] 是雅可比行列式,有 \(\operatorname{det} D \phi(r, \varphi)=r\)
其中 \(r, \varphi\) 是极坐标
圆柱坐标
\[ \phi:\left\{\begin{aligned} \mathbb{R}_{>0} \times[0,2 \pi[\times \mathbb{R}& \rightarrow & \mathbb{R}^{3} \backslash z \text { -axis } \\ \left(\begin{array}{c} r \\ \varphi \\ z \end{array}\right) & \mapsto\left(\begin{array}{c} x \\ y \\ z \end{array}\right)=\left(\begin{array}{c} r \cos \varphi \\ r \sin \varphi \\ z \end{array}\right) \end{aligned}\right. \]
其中 \[ D \phi(r, \varphi, z)=\left(\begin{array}{ccc} \cos \varphi & -r \sin \varphi & 0 \\ \sin \varphi & r \cos \varphi & 0 \\ 0 & 0 & 1 \end{array}\right) \] 是雅可比行列式,有 \(\operatorname{det} D \phi(r, \varphi, z)=r\),
其中 \(r,\varphi, z\) 是圆柱坐标 cylindrical coordinates
球坐标
$$ :{ \[\begin{aligned} \mathbb{R}_{>0} \times[0,2 \pi[\times ]0,\pi[& \rightarrow & \mathbb{R}^{3} \backslash z \text { -axis } \\ \left(\begin{array}{c} r \\ \varphi \\ \vartheta \end{array}\right) &\mapsto\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=\left(\begin{array}{c} r \cos \varphi \sin \vartheta \\ r \sin \varphi \sin \vartheta \\ r \cos \vartheta \end{array}\right) \end{aligned}\]. $$
雅可比行列式 \[ D \phi(r, \varphi, \vartheta)=\left(\begin{array}{ccc} \cos \varphi \sin \vartheta & -r \sin \varphi \sin \vartheta & r \cos \varphi \cos \vartheta \\ \sin \varphi \sin \vartheta & r \cos \varphi \sin \vartheta & r \sin \varphi \cos \vartheta \\ \cos \vartheta & 0 & -r \sin \vartheta \end{array}\right) \] 其中 \(\operatorname{det} D \phi(r, \varphi, z)=-r^{2} \sin \vartheta\)
其中 \(r, \varphi, \vartheta\) 是坐标
根和极值
高维空间的牛顿法
选择一个贴近的 \[\boldsymbol{x}^{*}\] 开始点 \(\boldsymbol{x}_{0} \in D\)
只要 \(\| \boldsymbol{x}_{k+1}-\boldsymbol{x}_{k} \| \geq \varepsilon\) 且 \(\left\|\left(D f\left(\boldsymbol{x}_{k}\right)\right)^{-1} f\left(\boldsymbol{x}_{k+1}\right)\right\| \leq\left\|\left(D f\left(\boldsymbol{x}_{k}\right)\right)^{-1} f\left(\boldsymbol{x}_{k}\right)\right\|\) 时
计算 \[ \boldsymbol{x}_{k+1}=\boldsymbol{x}_{k}-\Delta \boldsymbol{x}_{k}, \text{with }D f\left(\boldsymbol{x}_{k}\right) \Delta \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k}\right), k=0,1,2, \ldots \]
若 \[\operatorname{det} D f\left(\boldsymbol{x}^{*}\right) \neq 0\] 则存在根在附近,可以用这个来逼近 \[ \boldsymbol{x}_{0} \in U, \boldsymbol{x}_{k+1}=\boldsymbol{x}_{k}-\left(D f\left(\boldsymbol{x}_{k}\right)\right)^{-1} f\left(\boldsymbol{x}_{k}\right), k=0,1,, 2, \ldots \]
极值Optima
对于标量函数
全局最大值
global maximum \[ f\left(\boldsymbol{x}_{0}\right) \geq f(\boldsymbol{x}), \forall \boldsymbol{x} \in D \]
全局最小值
\[ f\left(\boldsymbol{x}_{0}\right) \leq f(\boldsymbol{x}), \forall \boldsymbol{x} \in D \]
局部最大值
\[ \exists \varepsilon>0: f\left(\boldsymbol{x}_{0}\right) \geq f(\boldsymbol{x}), \forall \boldsymbol{x} \in B_{\varepsilon}\left(\boldsymbol{x}_{0}\right) \]
局部最小值
\[ \exists \varepsilon>0: f\left(\boldsymbol{x}_{0}\right) \leq f(\boldsymbol{x}), \forall \boldsymbol{x} \in B_{\varepsilon}\left(\boldsymbol{x}_{0}\right) \]
上面不等号如果是 \(<,>\) 那么就是严格的strict
我们可以令梯度为 \(\boldsymbol{0}\) 来求 \[ \boldsymbol{x}_{0} \in D: \nabla f\left(\boldsymbol{x}_{0}\right)=\mathbf{0} \]
判断最值种类
如果 \(H_{f}\left(\boldsymbol{x}_{0}\right)\) 是负数,那么是局部最大值
如果 \(H_{f}\left(\boldsymbol{x}_{0}\right)\) 是正数,那么是局部最小值
如果 \(H_{f}\left(\boldsymbol{x}_{0}\right)\) 是 indefinite 那么是 saddle point
如果 \(H_{f}\left(\boldsymbol{x}_{0}\right)\) 是 semi-definite 那么无法判断
曲线和曲面
曲线
曲线是映射 \[ \gamma: I \subseteq \mathbb{R} \rightarrow \mathbb{R}^{n}, \text { with } \gamma(t)=\left(\begin{array}{c} x_{1}(t) \\ \vdots \\ x_{n}(t) \end{array}\right) \]
曲面
一个(带参数) 的平面是一个连续的,部分连续且可微分的函数 \[ \phi: B \subseteq \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}, \text { with } \phi(u, v)=\left(\begin{array}{c} x(u, v) \\ y(u, v) \\ z(u, v) \end{array}\right) \]
求面积Quadrature
高纬度求面积
曲面和体积积分
\(f: D=[a, b] \times[c, d] \rightarrow \mathbb{R}\) 可以定义下面的积分 \[ \iint_{D} f(x, y) \mathrm{d} x \mathrm{~d} y=\int_{c}^{d} \int_{a}^{b} f(x, y) \mathrm{d} x \mathrm{~d} y=\int_{c}^{d}\left(\int_{a}^{b} f(x, y) \mathrm{d} x\right) \mathrm{d} y \]
\[ \iint_{D} f(x, y) \mathrm{d} y \mathrm{~d} x=\int_{a}^{b} \int_{c}^{d} f(x, y) \mathrm{d} y \mathrm{~d} x=\int_{a}^{b}\left(\int_{c}^{d} f(x, y) \mathrm{d} y\right) \mathrm{d} x \]
Fubini定理
如果函数是连续的,那么积分的顺序不影响最终结果
标准定义域
\[ D=\{(x, y) \mid a \leq x \leq b, l(x) \leq y \leq u(x)\} \]
或者 \[ D=\{(x, y) \mid c \leq y \leq d, l(y) \leq x \leq u(y)\} \] 其中 \(l,u\) 是下界函数和上界函数
三维空间可以推广成 \[ D=\{(x, y, z) \mid a \leq x \leq b, l(x) \leq y \leq u(x), \tilde{l}(x, y) \leq z \leq \tilde{u}(x, y)\} \]
计算积分
对于标准定义域 \(B\) \[ B=\{(x, y) \mid a \leq x \leq b, l(x) \leq y \leq u(x)\} \] 计算积分可以这样求 \[ \int_{B} f=\int_{x=a}^{b} \int_{y=l(x)}^{u(x)} 1 \mathrm{~d} y \mathrm{~d} x=\int_{x=a}^{b}(u(x)-l(x)) \mathrm{d} x=\int_{x=a}^{b} u(x) \mathrm{d} x-\int_{x=a}^{b} l(x) \mathrm{d} x \]
坐标变换
设\(\phi: B \rightarrow D\) 是一个坐标变换 \[ \int_{D} f\left(x_{1}, \ldots, x_{n}\right) \mathrm{d} x_{1} \cdots \mathrm{d} x_{n}=\int_{B} f\left(\phi\left(y_{1}, \ldots, y_{n}\right)\right)\left|\operatorname{det} D \phi\left(y_{1}, \ldots, y_{n}\right)\right| \mathrm{d} y_{1} \cdots \mathrm{d} y_{n} \]
曲面积分
对于一个曲面 \[ \phi: B \subseteq \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}, \text { with } \phi(u, v)=(x(u, v), y(u, v), z(u, v))^{\top} \] 对于标量函数,我们定义 \[ \iint_{\phi} f \mathrm{~d} s=\iint_{B} f(\phi(u, v))\left\|\phi_{u}(u, v) \times \phi_{v}(u, v)\right\| \mathrm{d} u \mathrm{~d} v \] 对于向量函数,我们定义 \[ \iint_{\phi} \boldsymbol{v} \cdot \mathrm{d} s=\iint_{B} \boldsymbol{v}(\phi(u, v))^{\top}\left(\phi_{u}(u, v) \times \phi_{v}(u, v)\right) \mathrm{d} u \mathrm{~d} v \]
Gauss’s divergence theorem
\[ \iiint_{B} \operatorname{div} \boldsymbol{v} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z=\iint_{\partial B} \boldsymbol{v} \cdot \mathrm{d} s \]
高维求面积的应用
统计:计算moments
对于函数 \[f(x): D \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}, x=\left(\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right)\] 关于 \(c\) 的 \(q\)-th moments可以这样计算: \[ \mu_{q}=\int_{-\infty}^{\infty}(x-c)^{q} f(x) d x \]
机器学习
估计函数: \[ \hat{f}_{h}(x)=\frac{1}{n} \sum_{i=1}^{n} \mathcal{K}\left(\frac{x-x_{i}}{h}\right) \] 最小化 mean integrated squared error (MISE) \[ \text { MISE }=\mathbb{E}\left[\int\left(\hat{f}_{h}(x)-f_{h}(x)\right) d x\right] \]
偏微分方程
1阶偏微分方程
我们现在只考虑2个变量的情况, \(u=u(x, y)\) \[ a u_{x}+b u_{y}=f(x, y), \quad a, b \in \mathbb{R} \] 它的更一般的情况是:
线性1阶偏微分方程
\[ a(x, y) u_{x}+b(x, y) u_{y}=0 \]
类线性1阶偏微分方程
\[ a(x, y, u(x, y)) u_{x}+b(x, y, u(x, y)) u_{y}=c(x, y, u(x, y)) \]
2阶偏微分方程
Laplace Equation
\[ -\Delta u=0 \]
Maxwell's equations
\[ \nabla E=\frac{\rho}{\varepsilon_{0}}, \nabla B=0, \nabla \times E=-\frac{\partial B}{\partial t}, \nabla \times B=\mu_{0} j+\mu_{0} \varepsilon_{0} \frac{\partial E}{\partial t} \]
建模和仿真
第一部分:数学建模入门
术语
- 模型model: image of a reality
- 数学建模 Mathematical Modeling : 衍生derivation和分析analysis数学模型的过程
- 仿真 Simulation: 用模型实施的虚拟实验
仿真的目标
- 理解和重构一个场景
- 优化已知的场景
- 预测未知的场景
仿真步骤The Simulation Pipeline
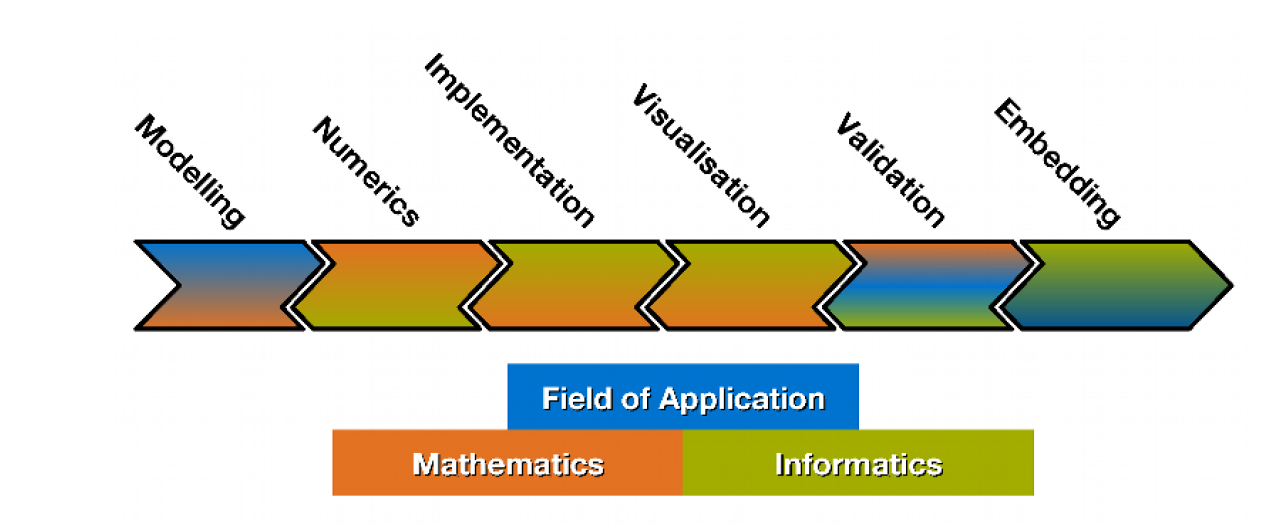
模型的衍生Derivation of Models
什么应该被建模
什么量比较重要,它起到了什么影响
重要的模型参数之间有什么联系
用什么工具来表达交叉和依赖关系
描述工具
用来表示交叉和依赖关系
- 代数方程
- 常微分方程
- 偏微分方程
- 自动机和传递图
- 图
- 概率分布
- Fuzzy logic
- 神经网络
仿真任务
什么是具体的任务
分析模型
关于可管理性和可解决性:
- 存在解
- 解是否唯一
- 对于数据的条件 continous dependency
well posed Problems
well posed 的意思是存在唯一稳定的解
但是大部分的问题都是 ill posed
模型的应用
这个模型可以被计算机解决吗
解决问题的方法
- Analyic 证明存在性和唯一性,并且直接构造解
- Heuristic 用某个策略尝试
- 数值算法
- 渐进数值算法
模型评估
- 这个模型是正确的吗
- 这个模型有多准确
模型的分类
- 离散和连续
- 确定的或随机的
规模和层次
不会是一次建成的模型,而是由层次的模型
第二部分:决定模型:博弈论,策略,选举
一般决定模型
决定会在
- 确定性
- 风险
- 不确定性
中决定
模型
一个决策者或者玩家 \(S\)
\(m\) 个可选择的动作/策略 \(A_1, ... A_m\)
\(n\) 个可能的开始状态 \(s_1,..s_n\)
在状态 \(s_i\) 做决策 \(A_i\) 的代价 \(N_{ij}\)
代价矩阵 \[ N=\left(N_{i j}\right)_{1 \leq i \leq m, 1 \leq j \leq n} \]
确定性时的选择:
选择\(\hat{i} \in\{1, \ldots, m\}\) 使得 \(N_{\hat{i} j}=\max _{i} N_{i j}\)
不确定时的选择
小心谨慎的选择(max-min payoff) \[ N_{\hat{i} j_{\hat{i}}}=\max _{i} \min _{j} N_{i j} \]
冒险的选择 (max-max payoff) \[ N_{\hat{i} j_{\hat{i}}}=\max _{i} \max _{j} N_{i j} \]
另一种谨慎(min-max payoff) \[ R_{\hat{i} j_{\hat{i}}}=\min _{i} \max _{j} R_{i j} \] 其中 \(N_{j}=\max _{i} N_{i j}\) 是状态 \(j\) 的代价\(R_{i j}=N_{j}-N_{i j}\) 是在状态 \(j\) 选 \(i\) 的风险
两个玩家零和游戏
\(S_1\) 是赢的玩家,有 \(m\) 种选择 \(A_1,...A_m\)
\(S_2\) 是输的玩家,有 \(n\) 种选择 \(B_1, ... , B_n\)
评估 \(S_1\) 选择 \(i\) 和 \(S_2\) 选择 \(j\) :
\(a_{i,j}\) 是 \(S_2\) 给 \(S_1\) 的payoff
两者交替行动的决策: \[ \begin{aligned} &S_{1}: A_{i} \Rightarrow S_{2}: B_{j_{i}}, a_{i, j_{i}}=\min _{j} a_{i j} \\ &S_{2}: B_{j} \Rightarrow S_{1}: A_{i_{j}}, a_{i_{j}, j}=\max _{i} a_{i j} \end{aligned} \]
假设两者都选择小心行动:
\(S_1\) 最大化保证的收益 \[ a_{\hat{i}, j_{\hat{i}}}=\max _{i} \min _{j} a_{i j} \]
\(S_2\) 最小化保证的损失 \[ a_{i_{\hat{j}}, \hat{j}}=\min _{j} \max _{i} a_{i j} \]
equilibrium 和 saddle point
\[ \max _{i} \min _{j} a_{i j}=a_{\hat{i}, \hat{j}}=\min _{j} \max _{i} a_{i j} \]
团队决定
\(A\) 是所有竞选者的集合
\(I\) 是所有投票者的集合
\(r: A \rightarrow \mathbb{N}\) 是排名
好感关系
\[ x \varrho y: \Leftrightarrow r(x)<r(y) \]
民主基本规则
\(K\) 对于所有 \(P_A^n\)
\(K\) 都在 \(A\) 里
Pareto condition \[ \left(\forall i \in\{1, \ldots, n\}: x \varrho_{i} y\right) \Rightarrow x \varrho y \] supremacy of the collective: the entirety can always enforce any desired ranking \(\varrho\) through unanimity.
Independence of irrelevant alternatives: ballots with identical ranking w.r.t. \(x\) and \(y\) must yield the same collective ranking w.r.t. \(x\) and \(y\).
exclusion of a dictator: no voter can always prevail
Arrow's impossible theorem
不可能同时满足上面5个条件
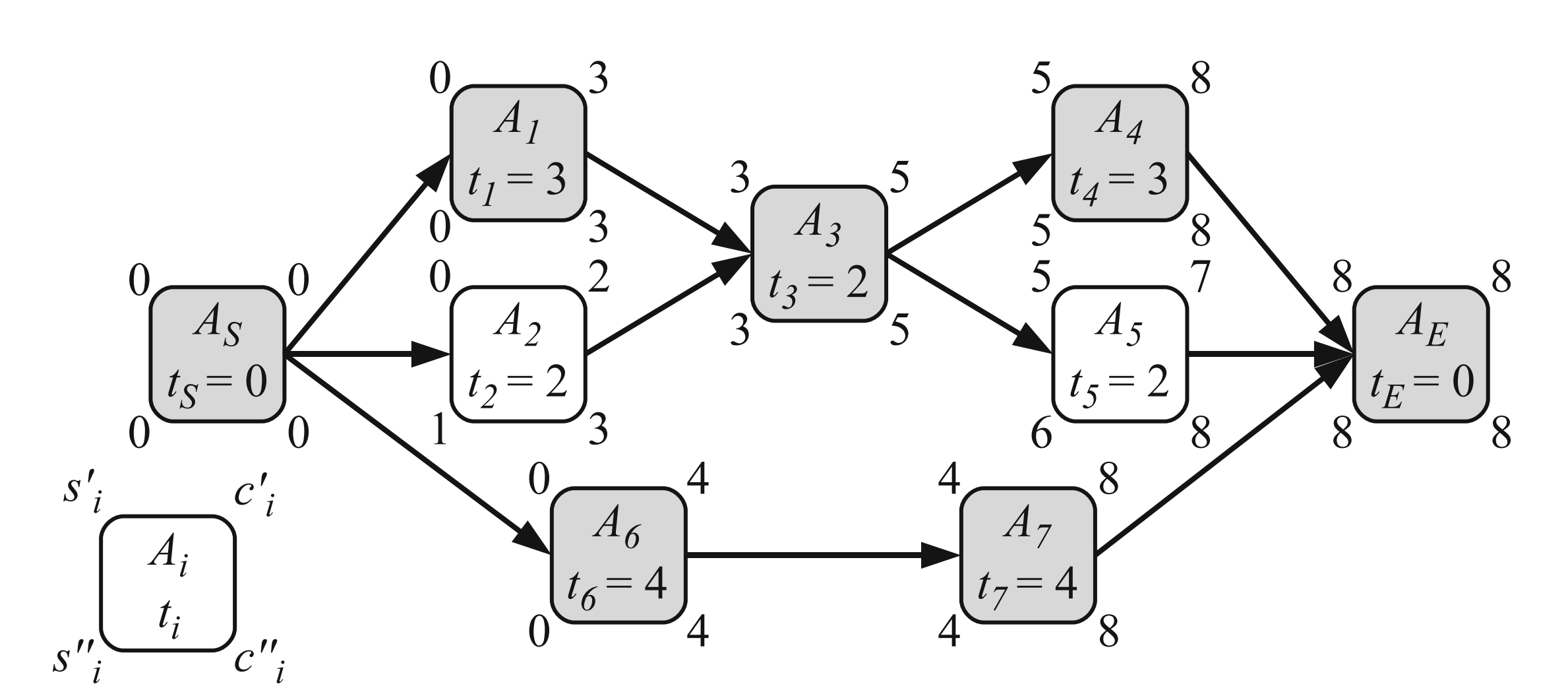
时序安排 Scheduling
有 \(n\) 个任务 \(A_1,...,A_n\)
有 \(m\) 台机器 \(M_1,...,M_m\)
\(t_i^{(j)}\) 是任务 \(i\) 在 \(j\) 机器上跑需要的时间
任务 \(i\) 的开始时间 \(s_i\), 完成时间 \(c_i = s_i + t _i\)
有依赖关系 \(A_i \rightarrow A_j\) 表示 \(A_i\) 必须完成$ A_j$ 才能开始
首先假设机器总是足够的
\(s_i'\) 是最早开始时间
\(c_i'\) 是最早完成时间
\(s_i''\) 是最晚开始时间
\(c_i''\) 是最晚完成时间
\(s_i'=s_i''\) 的点是 critical poing
critical path是从起点到终点的critical point的路径
它决定最终完成时间
Job-Shop Problem
神经网络
学习过程:网络权值的适应性改变
free learning task
给定输入,求输出
学习过程完成,若根据输入可以给出相似的输出
fixed learning task
输入和输出都给定
学习过程是自己完成的
学习算法:
- 监督学习: 解决fixed learning task
- 非监督学习: 解决 free learning task
测量误差
对于单个输出 \(u \in U_{O}\) \[ e_{u}:=t_{u}-o_{u} \] 对于整个网络 \[ e:=\sum_{u \in U_{O}}\left(t_{u}-o_{u}\right)^{2} \]
监督学习的基本结构
- 选择 pattern pair \((i,t)\)
- 传播输入直到停止
- 对比输出和目标输出,然后计算误差
- 如果误差不是0,那么调整参数
- 在处理完所有输入后,如果误差可以接受那么成功,否则失败
非监督学习的基本结构
- 选择学习任务 \(i\)
- 传播输入直到停止
- 改变网络结构根据修改标准
- 到所有输入处理完后,最后停止
多层感知器
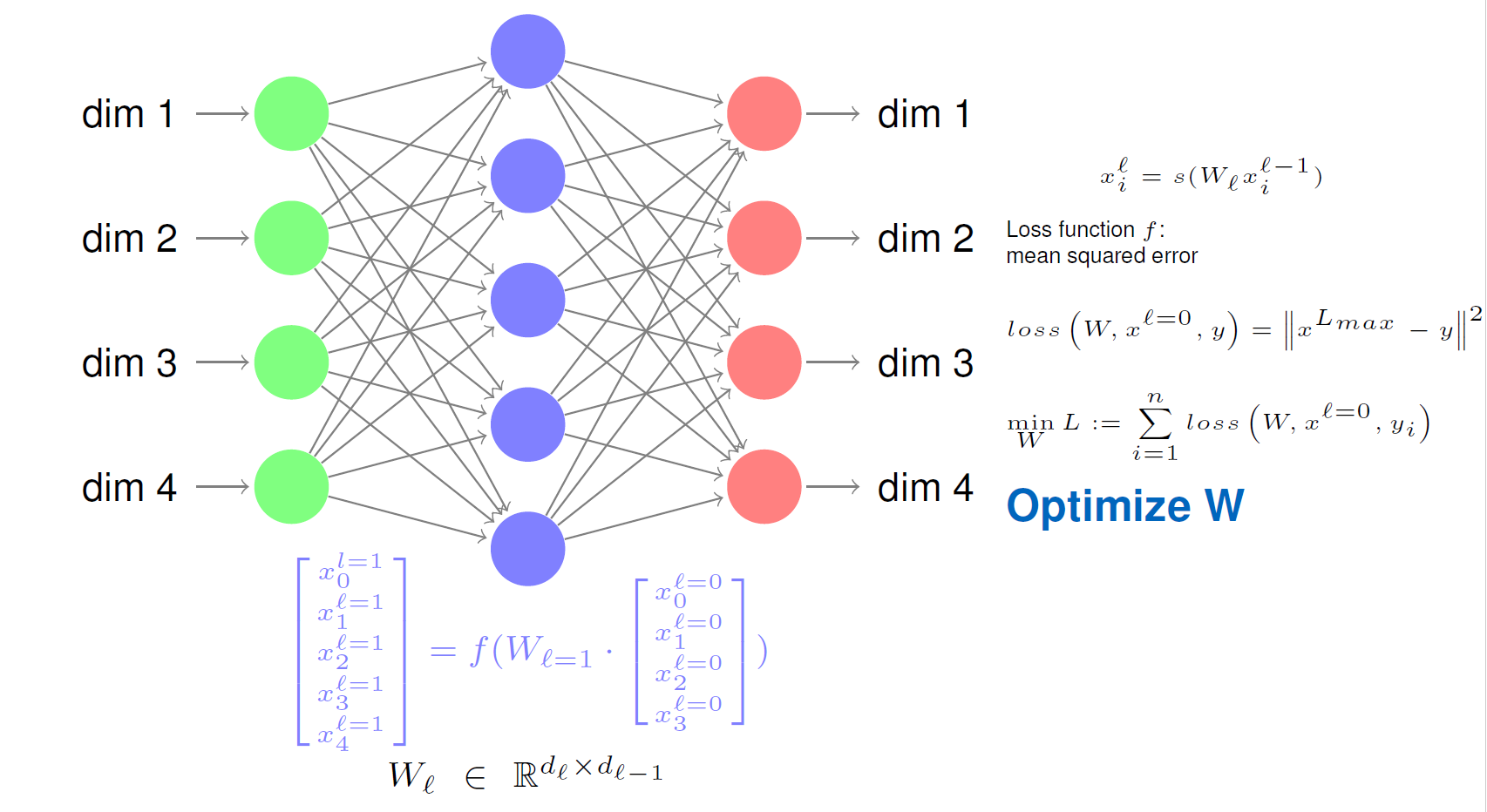
反向传递
测量误差 \[ E:=\sum_{i} E^{(i)}:=\frac{1}{2} \cdot \sum_{i} \sum_{v \in U_{n}}\left(t_{v}^{(i)}-a_{v}^{(i)}\right)^{2} \]
数值动态模型
总体动态模型
解homogene的ODE
已知 \(A \in \mathbb{R}^{n \times n} . b \in \mathbb{R}^{n}, x(t): \mathbb{R} \rightarrow \mathbb{R}^{n}\) 求下面ODE的通解 \[ \dot{x}(t)=A x(t) \] 首先求Eigenvector \(v_i\)和对应的Eigenvalues \(\lambda_i\) \[ \lambda A = \lambda I \] 解出所有 \(\lambda _i\)
然后对每个 \(\lambda_i\) , 带入 \(A - \lambda_i I\) 得出 \(M\) \[ M v_i = \lambda_i v_i \] 解出 \(v_i\) \[ x(t)=\sum_{i=1}^{n} c_{i} e^{\lambda_{i} t} v_{i} \]
解nonhomogene 的ODE
已知 \(A \in \mathbb{R}^{n \times n} . b \in \mathbb{R}^{n}, x(t): \mathbb{R} \rightarrow \mathbb{R}^{n}\) 求下面ODE的通解 \[ \dot{x}(t)=A x(t) - b \] 首先求Eigenvector \(v_i\)和对应的Eigenvalues \(\lambda_i\)
然后解一个平衡点的解 \[ 0=\dot{x}_{i}=\lambda_{i} x_{i}-b_{i} \]
\[ \hat{x}_{i}=\frac{b_{i}}{\lambda_{i}} \]
令 \(\hat{b}\) 是 \(b_i /\lambda_i\) 的向量
然后解是 \[ x(t)=\sum_{i=1}^{n} c_{i} e^{\lambda_{i} t} v_{i} + \hat{b} \]
热能传递
用 PDE 建模
比如热能传递,这里的温度 \(T\) 是随着时间变化和位置变化的多维函数 \[ T(x ; t) \quad \text { or } \quad T(x, y ; t) \quad \text { or } \quad T(x, y, z ; t) \] 比如加热圆柱体
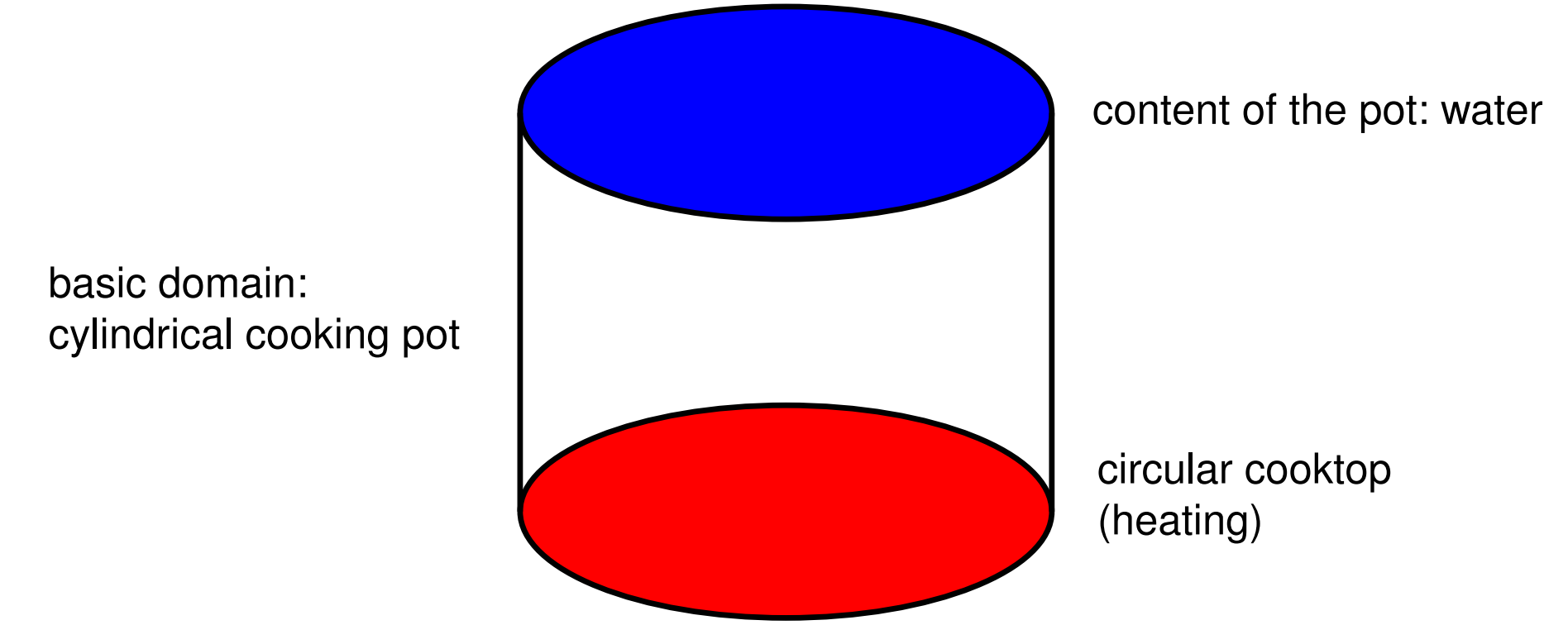
我们先写出热能方程 \[ \kappa \cdot\left(T_{x x}+T_{y y}+T_{z z}\right)=\kappa \cdot\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right)=\frac{\partial T}{\partial t}=T_{t} \] 用laplace operator \[ \Delta T:=T_{x x}+T_{y y}+T_{z z} \] 代换一下 \[ \kappa \cdot \Delta T=T_{t} \]
边界条件的种类
Dirichlet condition:温度是常数
Neumann condition:边界条件是可以从外部传递进入,是一个梯度 \[ \frac{\partial T}{\partial n}(t ; x, y, z)=\nabla T(t ; x, y, z) \cdot \vec{n}=\varphi(t ; x, y, z) \text { on } \partial \Omega \]
数值解决PDE
First Difference Method
对于 \[ \Omega \subseteq \mathbb{R}^{d}, d \in\{1,2,3\} \] 我们构造一个方格
\(h_x,h_y,h_z\) 是每个相邻点的间距 \[ h=\left(h_{x}, h_{y}, h_{z}\right) \]
交通流量模拟
随机过程
coeffificient of variation
\[ \varrho(T)=\frac{\sigma(T)}{E(T)} \]
hazard rate
\[ h_{T}(t)=\lim _{\Delta t \rightarrow 0} \frac{p(T \leq t+\Delta t \mid T>t)}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{F_{T}(t+\Delta t)-F_{T}(t)}{\left(1-F_{T}(t)\right) \cdot \Delta t}=\frac{f_{T}(t)}{1-F_{T}(t)} \]
FRT(VRZ)
当你随机处于一个时间 \(t\) 时候,你等到下一个车出现的时间是 FRT(Forward Remaining time)。你经过的时间是 BRT(Backward Remaining time) \[ E(FRT)=E(BRT)=\frac{E(T)}{2}\left(1+\varrho^{2}(T)\right) \]
wait time paradox 等待悖论
当 \(\varrho(T) >0\) 时,\(E(FRT) > E(T)\)


