密码学
密码学
理论基础
Alice 给 Bob 发消息,保护消息的 confidentiality. 传输途径可以是任意的,Internet, USB stick... 在过程中被动的监听者Eve 有可能会监听或者解释信息.
在过去,军事加密依赖于信息的混乱程度 obfuscation of message contents. 现代密码学依赖于 Kerckhoff's Principle, 除了key所有信息都是已知的.
A crypto system should be secure, even if everything about the system, except the key, is public knowledge.
信息加密是通过 encryption schemes 使用一个key和lock concept来实现的. 只有key的持有者可以加密解密信息. Alice会把key \(k\) 分享给Bob, 我们现在还不关系这个怎样实现.
- Alice 加密信息 \(m\), \(c := E(k,m)\)
- Bob 解密信息 \(m:=D(k,c)\)
香农密码 Shannon Cipher
我们定义一个 encryption scheme \(\Pi:=(E, D)\) 是一对加密解密函数
\(k \in \mathcal{K}\) 是加密使用的key
\(m \in \mathcal{M}\) 是信息 message
\(c \in \mathcal{C}\) 是密文 ciphertext
\(E: \mathcal{K} \times \mathcal{M} \rightarrow \mathcal{C}\) 是加密函数
\(D: \mathcal{K} \times \mathcal{C} \rightarrow \mathcal{M}\) 是解密函数
正确性: \(\forall k \in \mathcal{K}, m \in \mathcal{M}: D(k, E(k, m))=m\)
这个密码被称为 Shannon cipher.
One-time-pad (OTP)
OTP 是一个Shannon cipher. OTP 中 \(\mathcal{K}=\mathcal{M}=\mathcal{C}:=\{0,1\}^L\) 其中 \(L\ge 1\) 是长度. 我们可以简单证明它的正确性
证明 \[ D(k, E(k, m))=D(k, k \oplus m)=k \oplus(k \oplus m)=m \]
定义 1 完美安全 Perfect security
一个Shannon cipher \(\Pi=(E, D)\) over \((\mathcal{K}, \mathcal{M}, \mathcal{C})\) 是 perfectly secure 若 \[ \forall m_0, m_1 \in \mathcal{M}, c \in \mathcal{C}: \operatorname{Pr}\left[E\left(\mathbf{k}, m_0\right)=c\right]=\operatorname{Pr}\left[E\left(\mathbf{k}, m_1\right)=c\right] \] \(\mathbf{k}\) 是 random variable.
任取两个信息,密文是 \(c\) 的概率是相同的. 也就是可能是 \(m_0\) 也可能是 \(m_1\)
于是不可能从密文中获取任何信息. 我们一直假设 \(k\) 是完全随机选取的,每个 \(k\) 的概率是 \(\frac{1}{|\mathcal{K}|}\) 于是可以推出 \[ \operatorname{Pr}[E(k, m)=c]=\frac{N_{m, c}}{|\mathcal{K}|} \] 其中 \(N_{m,c}\) 是有多少个key 可以把 \(m\) 加密成 \(c\) \[ N_{m, c}=|\{k \in \mathcal{K}: E(k, m)=c\}| \] 所以有另一个等价的定义: \[ \forall m_0, m_1 \in \mathcal{M}, c \in \mathcal{C}: N_{m_0, c}=N_{m_1, c} \] 对于任意两个信息,能把 \(m_0\) 变成 \(c\) 和能把 \(m_1\) 变成 \(c\) 的key个数相同
- 即使Perfectly secure 的密码也可能被破解,如果使用不当,比如OTP只能用1次.
定理 1 OTP perfectly secure
The one-time pad is perfectly secure.
因为对于所有 \(m \in \mathcal {M}\) 只有1个 key 使得 \(E(k,m)=c\) 也就是 \(N_{m,c}=1\) .
证明
假设有两个 key \(k_0,k_1\) 使得 \(E(k_0,m)=E(k_1,m)=c\) 那么 \[ \begin{aligned} E\left(k_0, m\right) & =E\left(k_1, m\right) \\ k_0 \oplus m & =k_1 \oplus m \\ k_0 \oplus m \oplus m & =k_1 \oplus m \oplus m \\ k_0 & =k_1 \end{aligned} \] 所以这两个是一样的,
但在使用中,如果要通讯 1GB, 那么你需要交换 1GB 的密钥. 那还不如只交换信息.
定理 2 Shannon's Theorem
If \(\Pi=(E, D)\) 是 perfectly secure, then \(|\mathcal{K}| \geq|\mathcal{M}|\)
证明
假设 \(|\mathcal{K}| < |\mathcal{M}|\) 那么选择一个信息和密钥 \(\operatorname{Pr}\left[E\left(\mathbf{k}, m_0\right)=c\right]>0\) 然后设 \(S\) 是所有 \(c\) 的解密集合. \(S=\{D(\hat{k}, c) \in \mathcal{M}: \hat{k} \in \mathcal{K}\}\) 有 \(|S| \leq|\mathcal{K}|<|\mathcal{M}|\) 那么我们选择 \(m_1 \in \mathcal{M} \backslash S\) 所以\(m_1\) 不是 \(c\) 的解密。那么 \(c\) 也不是 \(m_1\) 的加密,因为如果是的话根据正确性一定是解密。所以 \(\operatorname{Pr}\left[E\left(\mathbf{k}, m_1\right)=c\right]=0\) 所以不能被加密或解密。所以找到了一个不同的概率。
所以 perfect security 是不可实现的 not practical. 我们需要一个高效的算法使得我们的密码被高效破译的可能性忽略不计.
定义 2 PPT adversary
一个对手 adversary \(\mathcal{A}\) 是高效的 efficient, 若它可以在多项式时间内完成计算 polynomially-bounded time. 我们称它为 probabilistic polynomial time (PPT)-adversary.
定义 3 polynomially-bounded
一个函数 \(f: \mathbb{Z}_{+} \rightarrow \mathbb{R}\) 是 polynomially-bounded 若存在 \(c\in \mathbb{N}\) 使得对于所有整数 \(n \geq n_0\), we have \(|f(n)| \leq n^c\left(f(n) \in \mathcal{O}\left(n^c\right)\right)\)
定义 4 negligible
一个函数 \(f: \mathbb{Z}_{+} \rightarrow \mathbb{R}\) 是 negligible 若对于所有 \(c\in \mathbb{N}\) 存在 \(n_0 \in \mathbb{Z}_{+}\) 使得对于所有整数 \(n \geq n_0\) 有 \(|f(n)| \leq \frac{1}{n^c}\left(f(n) \in \mathcal{O}\left(\frac{1}{n^c}\right)\right)\)
定义 5 super-poly
一个函数 \(f: \mathbb{Z}_{+} \rightarrow \mathbb{R}\) 是 super-poly 如果 \(\frac{1}{f}\) 是negligible.
计算法则
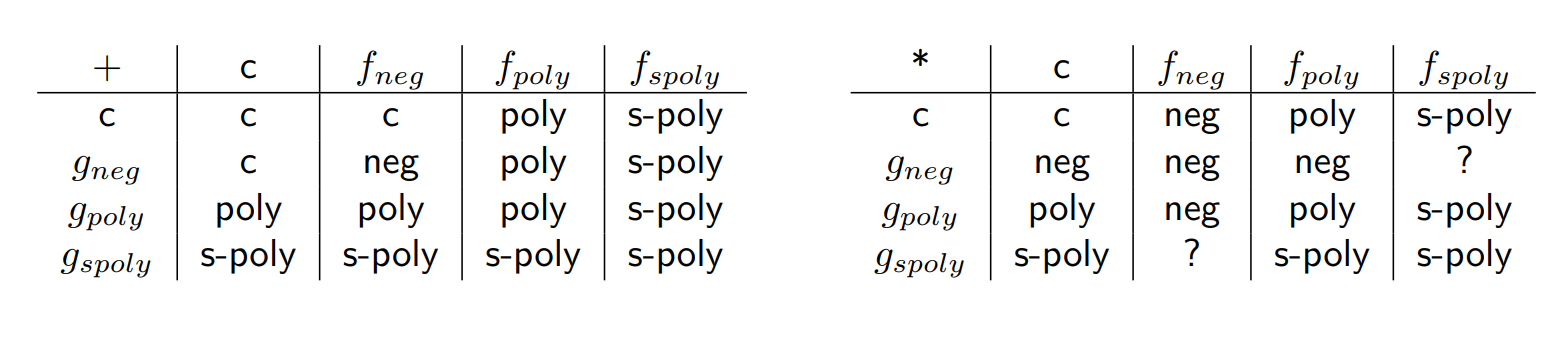
安全参数 Security Parameters
- Security parameter \(\lambda\) 是一个正整数
它在密码部署的时候选择,等级越高,安全系数越高. 越高意味着更长的key和更慢的 \(D,E\) 运行时间
- System parameter \(\Lambda\) 是一个bit string
是被 \(\lambda\) 选择的. 比如是一个模数用于取模.
定义 6 Efficient Algorithm
\(A\) 是一个算法,输入一个 security parameter \(\lambda\) 和其他的参数. 他们被表示为一个bit string \(x \in\{0,1\}^{\leq p(\lambda)}\) 其中 \(p\) 是一个fixed polynomial. 那么我们说 \(A\) 是efficient algorithm 若存在一个 poly-bounded function \(t\) 和一个可以忽略的参数 negligible function \(\epsilon\) 使得对于所有的 \(\lambda,x\) 这个运行时间超过 \(t(\lambda)\) 的概率最多是 \(\epsilon(\lambda)\)
定义 7 Computational Cipher
我们定义一个 computational cipher 是一对高效算法 \((E, D)\) 是一对加密解密算法
\(k \in \mathcal{K}\) 是加密使用的key
\(m \in \mathcal{M}\) 是信息 message
\(c \in \mathcal{C}\) 是密文 ciphertext
\(E: \mathcal{K} \times \mathcal{M} \rightarrow \mathcal{C}\) 是加密算法
\(D: \mathcal{K} \times \mathcal{C} \rightarrow \mathcal{M}\) 是解密算法
\(\mathcal{K,M,C}\) 是有限的空间
我们的加密算法有可能是 prababilistic 的,也就是对于给定的 \(k,m,E(k,m)\) 可能会有很多结果. \[ c \stackrel{R}{\leftarrow} E(k, m) \] 正确性可以这样写: \[ \forall c \stackrel{R}{\leftarrow} E(k, m): D(k, c)=m \] 所有deterministic cipher都是 Shannon cipher.
然而 Shannon cipher不一定是 computational cipher (不一定高效算法)
反过来也不一定 (有可能是prababilistic)
computaional cipher 的安全性
有可能没有 \(m_0\) 加密成 \(c\) 所以我们令 \[ \left|\operatorname{Pr}\left[\phi\left(E\left(\mathbf{k}, m_0\right)\right)\right]-\operatorname{Pr}\left[\phi\left(E\left(\mathbf{k}, m_1\right)\right)\right]\right| \leq \epsilon \] 我们可以通过 Attack Game 来定义 \(\epsilon\)
Attack Game 1
我们有2个Experiment 0, 1 对于 \(b \in\{0,1\}\) 我们定义 Experiment \(b\)
- 对手计算 \(m_0,m_1\in \mathcal{M}\) 长度相同,给chanllenger
- challenger 计算 \(k \stackrel{R}{\leftarrow} \mathcal{K}, c \stackrel{R}{\leftarrow} E\left(k, m_b\right)\) 然后把 \(c\) 发给对手
- 对手猜测 \(m_{\hat{b}}=D(k, c)\) 是哪一个信息.
我们定义 \(\mathcal{A}\) 的 semantic security advantage 为 \[ S C a d v[\mathcal{A}, \Pi]:=\left|\operatorname{Pr}\left[W_0\right]-\operatorname{Pr}\left[W_1\right]\right| \]
定义 8 semantic security
一个 cipher 是 semantically secure 若 \(Scadv[\mathcal{A},\Pi]\) 对于所有 PPT 对手是可忽略不计的 negligible.


