知识点

枚举

cnt枚举2个量

在一个数组中, \(cnt[x]\) 代表 \(x\) 出现的次数 \[ \sum_x cnt[x] \le n \] 于是可以枚举所有 \(x\) 在枚举所有小于 \(cnt[x]\) 的数，总复杂度不超过 \(O(n)\)

CF1637E(2100)

枚举 \(2^k\)

长度是 \(2^k\) 那么直接枚举 \(k\) 即可

CF1626D(2100)

二分

同时检查多个参数:

用二进制表示，0表示不符合，1表示符合，放到一个集合里，再枚举集合

zone2021_c

对 $x_i \(找下一个不超过\)L$ 的点，可以用lowerbound查询

倍增dp

arc060_c

整体二分

CF1601C

并查集

对于两者选1的问题，用边建图，然后分析。

arc111_b

数据结构，小的向大的合成可以降低复杂度

abc183_f

神奇构造

分式 \[ \frac{1}{x(x+1)} = \frac{1}{x} - \frac{1}{x+1} \]

arc163c

拆分再组合

agc055_a

构造部分解，然后组合成最终解

循环构造

agc056_a

三角形数

\(1+2+..+k\) 的和

Fermat polygonal number theorem：

任意正整数可以拆分成不超过3个三角形数的和

扩展：

不超过7个三角形数，如果连续按最近的三角形数拆分 (验证正确 <= 1e8)

arc129_c

排序

如果交换任意两个位置，那么最小交换次数是 \(N-\#ring\) 环的数量.

ABC302G

数学

式子推导

平均值处理

\[ \frac{1}{k}\sum_{i=1}^k a_k \ge S \\ \Leftrightarrow \sum_{i=1}^k a_k \ge k\cdot S \\ \Leftrightarrow \sum_{i=1}^k (a_k-S) \ge 0 \]

ABC292Ex

个数限制

在

\[ \left \lfloor \frac{m}{1} \right \rfloor+\left \lfloor \frac{m}{2} \right \rfloor+...+\left \lfloor \frac{m}{m} \right \rfloor \le O(mlog(m)) \]

CF1657D

中，最多有 \[ 2\sqrt{m} \]

个不同的数

证明：

考虑 \(m/k\)

  • \(k>\sqrt{m}\) ，

    \[ \frac{m}{k} < \frac{m}{\sqrt{m}} = \sqrt{m} \]

    最多不超过 \(\sqrt{m}\) 个

  • \(k \le \sqrt{m}\), 设 \(t = \lfloor \frac{m}{k} \rfloor\) , 显然 \(t\ge k\)

    \[ \left \lfloor \frac{m}{\lfloor \frac{m}{k} \rfloor} \right \rfloor = k \]

    成立

    证明：

    \[ kt \le m < k(t+1) = kt+k \le kt+t = k(t+1) \\ kt \le m < t(k+1) \\ \left \lfloor \frac{m}{\lfloor \frac{m}{k} \rfloor} \right \rfloor = k \]

    一共不超过 \(\sqrt{m}\) 个

CF1603C

取模公式

\[ a \bmod b = a-b\cdot \lfloor \frac {a}{b} \rfloor \]

CF1553F

整除公式

\[ \begin{aligned} \lfloor \frac{a}{b} \rfloor&=0 , a\in [0,b) \\ \lfloor \frac{a}{b} \rfloor&=1 , a\in [b,2b) \\ ... \\ \lfloor \frac{a}{b} \rfloor&=k , a\in [kb,(k+1)\cdot b) \\ \end{aligned} \]

可以考虑贡献

CF1553F

平均分配 \(A_i\) 到 \(k\) 个数上 \[ \sum_{j=1} ^{k} \lfloor \frac{A_i+j-1}{k} \rfloor = A_i \]

agc053_a

因子个数上界

X的因子个数约为(近似值) \[ O(X^{\frac{1}{3}}) \]

arc124_c

组合数学

考虑最大的数，然后隔板法

arc116_c

容斥原理

需要用容斥原理的计数dp

agc046_b

卢卡斯定理

https://brilliant.org/wiki/lucas-theorem/#proof-of-the-theorem

CF1673B(2500)

概率期望

期望神奇化简公式 \[ E[X]=\sum_{i=1}^Mi \cdot Pr[X=i] = \sum_{i=1}^M Pr[X\ge i] \]

ABC295E

消元解期望

期望式子很复杂，但是到一段有解。可以列关于父亲的表达式，然后迭代上来解

1823F

FFT

先写出式子，右边界可以根据 \(i+j < |S|\) 来确定 \[ \min_{0\le i\le |S|-|T|} \sum_{j=0}^{|T|-1} s_{i+j} \oplus t_j \] 然后翻转 \(t\) , 令 \(j'=|T|-1-j\) 然后把 \(j=|T|-1-j'\) 代入，然后把 \(j'\) 用原来的符号 \(j\) 代替 \[ \min_{0\le i\le |S|-|T|} \sum_{j=0}^{|T|-1} s_{i+j} \oplus t_{|T|-1-j} \] 然后写出卷积的式子 \[ c_i = \sum_{j+k=i} s_j \oplus t_k \] 然后我们知道 \(i+j + |T|-1-j = i+|T|-1\) 所以 \[ c_{i+|T|-1}= \sum_{j=0}^{|T|-1} s_{i+j} \oplus t_{|T|-1-j} \] 然后用乘法更换xor操作, 也就是分成2个卷积计算
\[ a \oplus b = a(1-b) + b(1-a) \] 那么对于 \(c\) 来说，最终的下标是 \[ \min_{|T|-1\le i \le |S|-1} c_i \]

ABC196F, ABC290G

图论

完全图

欧拉路径构造

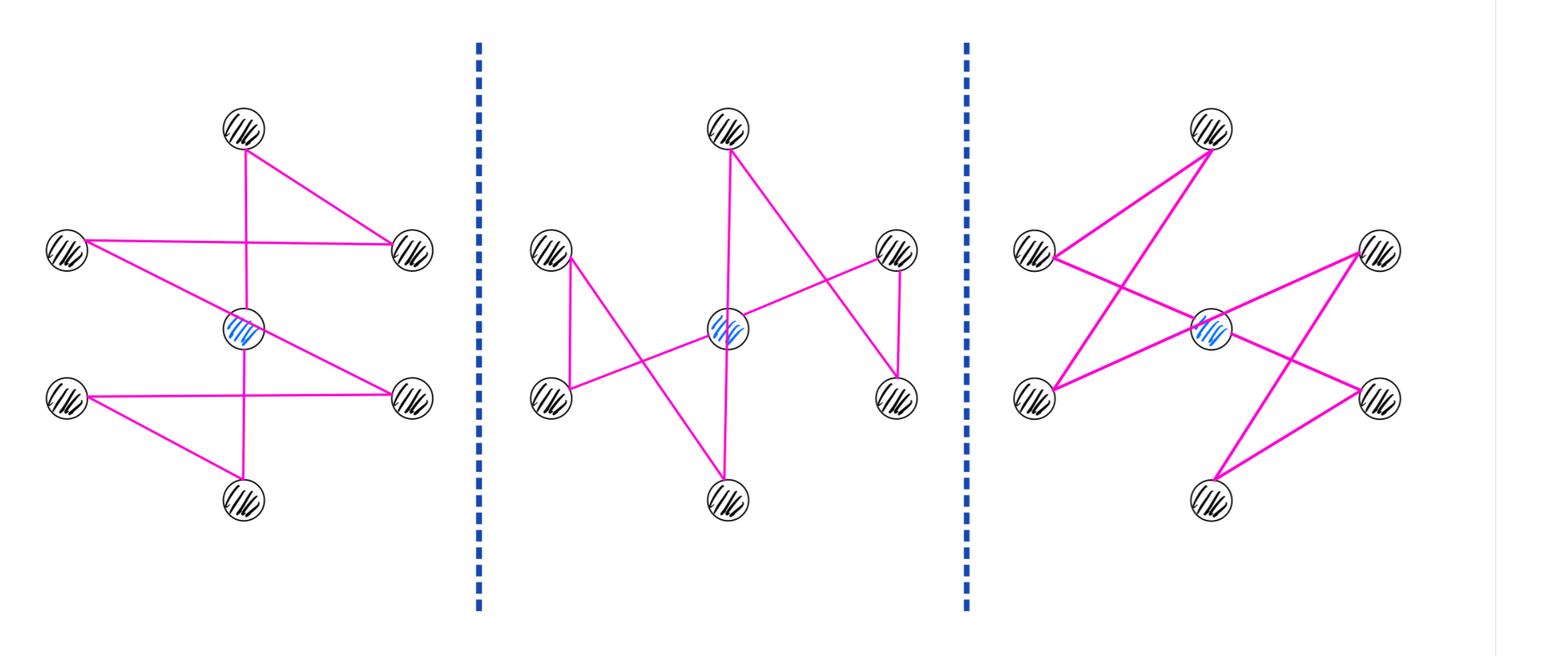
image-20211101223826968

https://codeforces.com/gym/103329/problem/D

最短路

01BFS

0的边权放在队列头，1的边权放在队列尾

abc213_e

Dijkstra

势能法处理负权

ABC237E

树

度数和树的等价关系 \[ \sum_{i=1}^N d_i=2(N-1) \]

计数

改变计数维度

考虑贡献：有多少个不同的答案，每个答案有多少贡献

CF1603C

找规律发现很多数字相同。把相同的数字分组，然后对组的和进行dp

ABC232E

把相同位置找出来，然后看有多少个符合的数。而不是枚举每个数看不同的位置

ABC295F

横着数改竖着数 \[ \sum_{X\in S}f(X) = \sum_{i=1}^N X\in S\and f(X_i) \]

ABC290F

利用对称性

\[ \sum_{i=1}^N f(X_i)= N\cdot f(X_1) \]

ABC290F

对所有子数组计数

找pair \((l,k,r)\) 看计算当前 \(k\) 的贡献

CF1827B2

环和链计数问题

链和单独点的计算方法不一样

  • 大于2 的链，先选两个端点（排序后，依次选后面的），然后再隔板法选
  • 单独点，单独选出来

gym104270L

随机算法

生日悖论

\[ P \approx 1-e^{-\frac{n(n-1)}{2 N}} \]

近似表达式，\(N=365,n=23\)

小数据可以暴力

CF1835C

Meet in the Middle

判断两个东西想等，把bit的数量减半

CF1835C

博弈论

状态转移dp

有2种选择，A会最大化结果，B会最小化结果。 A选择一个值，B减去这个值或加上这个值 \[ max_{x} \left( min(f_1+x,f_2-x) \right) \] \(f_1,f_2\) 已知, \(x \in [0,k]\) . 把 \(f_1+x,f_2-x\) 看成2个一次函数，那么最小值就是区下面的部分。再取最大值就是他们的交点 \[ x = \frac{f_2-f_1}{2} \] 这个时候 \[ y = f_1 + x = f_1+ \frac{f_2-f_1}{2} = \frac{f_1+f_2}{2} \] 可以证明 \(x\) 不会越出 \([0,k]\) 因为 \(x(n,m) = \frac{x(n-1,m)+x(n-1,m-1)}{2} \le k\) 所有不用考虑取模问题

CF1628D1(2100)

轮到A时候最大化A-B的分数，轮到B的时候最小化A-B的分数。然后可以dp这个A-B

abc201_d

SG定理和NIM游戏

通过对称推导, NIM游戏

CF1823E

二分图思维

每个状态有个对应的点，染2颜色。每次取不同颜色的一点可以。

CF11839E

数据结构

单调栈

处理区间的max和区间的min相关问题

线段树

线段树维护dp的一个维度

CF1842E

动态规划

数位DP

查找小于某个数的个数, 如果算第 \(i\) 个数很简单，那么可以二分.

ABC295F

Set 上DP

从大小 \(n-1\) 的set到 \(n\)

ARC147D TODO

二维dp

枚举两个端点的复杂度过大，可以考虑从一个点走到另一个点的dp

ABC210D

考虑一条路径，把空的块作为参数，然后就可以计算dp. 计算的时候，化简，然后把参数乘到dp里面去

keyence2021_c

区间dp

考虑贡献，别绕进去

cf1666j

DP状态优化

如果dp状态没法存下值

如果dp的答案很小，那么可以维护答案，和达到答案的所有集合

CF1824C

dp空间优化

答案是下凹函数，可以根据单调性把尾巴pop掉来优化空间

CF1830D

字符串

结论

$a^{inf} < b^{inf} a+b<b+a $

可以用扩展KMP计算

回文数

一个长度为 \(n\) 回文数由前 $$ 个字符决定。因此可以将问题简化为考虑前 $$ 个字符

ABC242E(1200)

个数统计

  • 已知 \(S\) ，且\(S,T\) 全是大写字母，统计 \(T\le S\) 的字符串个数。

可以用树状图画出统计路线

1
2
3
4
5
ll ans = 0;
for (int i = 1;i <= (n+1)/2; ++i) {
    ans = mul(ans, 26);
    ans = add(ans, s[i] - 'A');
}

数组排序问题

考虑逆序对个数的奇偶性

某操作不影响逆序对个数的奇偶性。多重数字，可以构造出合适的奇偶性。

ARC136B(1200)

多元方程组

设参数，是的方程组有唯一解。然后分析参数的限制。

ARC135B(1200)

计算几何

仿射变换

abc189_e

判断点在凸包内部

极角排序，然后二分

ABC296G

其他

异或哈希

判断子集包含的等价类

CF1830C

思维点

统计所有子数组的答案和

用子问题拆解，然后dp

只要定义好状态，可以简化很多代码。

ABC242D(1200)

Ad_hoc

某些特殊情况发生的时候，答案可以很容易算出来，根据这个分类讨论

想的时候先搞清楚，什么是关键的条件

AGC062A