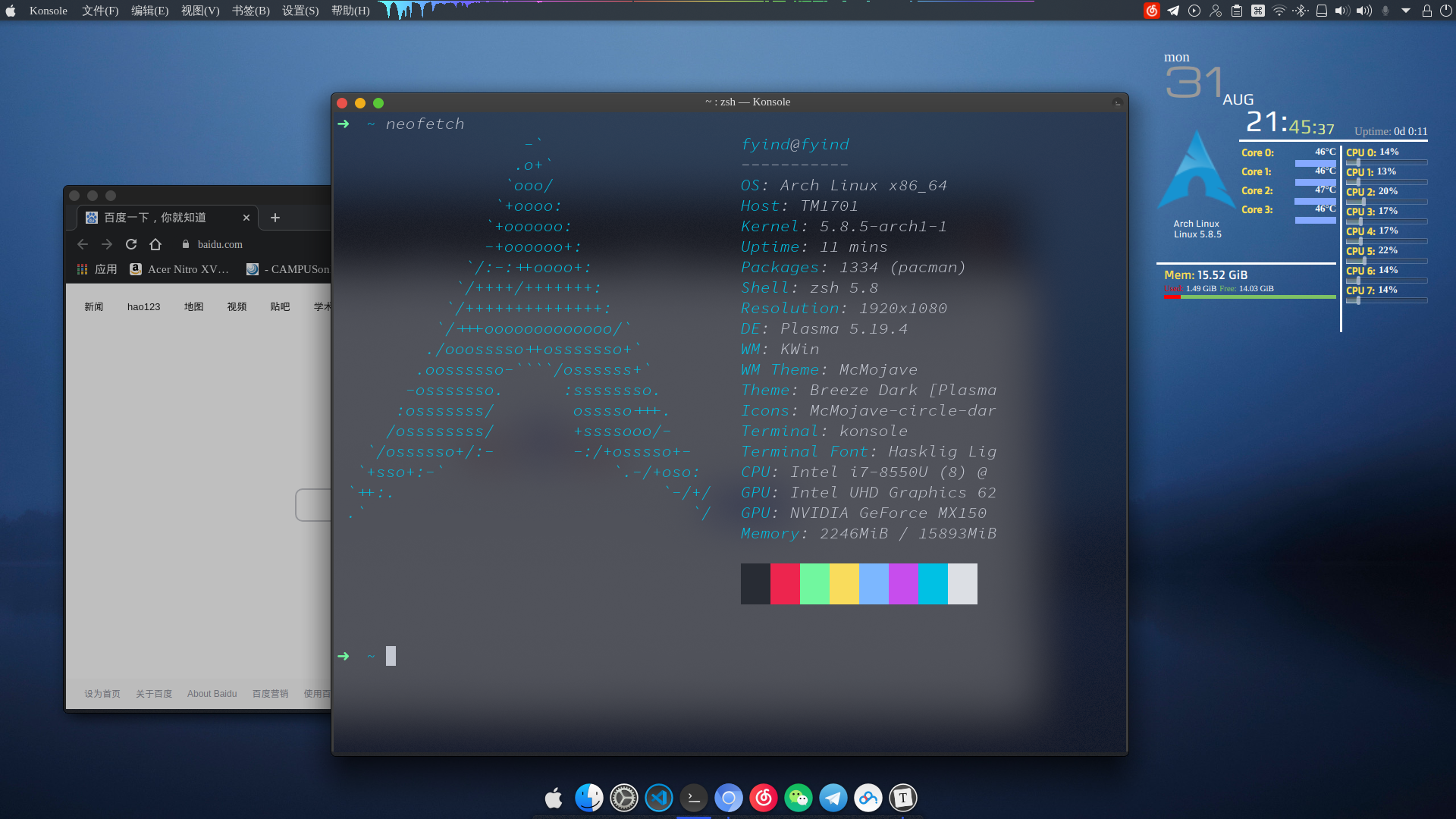
KDE安装和配置
KDE 安装和配置 image-20200831214423806 image-20200831214600617 这个是效果图 基础安装 首先安装完 Archlinux . 参见 Archlinux 完整安装过程 首先连上网络 虚拟机或网线 1dhcpcd WiFi 123systemctl start wpa_supplicant.servicenmcli dev wifi listnmcli dev wifi connect "ssid" password "passwd" 创建交换文件 申请 512M 的空间 12345dd if=/dev/zero of=/swapfile bs=1M count=512 status=progress chmod 600 /swapfilemkswap /swapfileswapon /swapfilevim /etc/fstab 然后在末尾添加 1/swapfile none swap defaults 0 0 添加用户 这里的 [username] 换成你想要的用户名, 然后是设...
算法模板集合
算法模板集合 [toc] 编译 1g++ name.cpp -Wall -Wextra --std=c++17 -o name; .\name.out 对拍 1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980import osfrom random import *my = 'm.exe'std = 'std.exe'class DSU: def __init__(self,n=0) -> None: self.fa = [-1]*(n+1) def find(self, x: int)->int: if self.fa[x] == -1: return x else: self.fa...
动态规划入门
动态规划入门(一) 动态规划(Dynamic Programming),简称dp,是算法竞赛中一种非常重要的解决问题的手段之一。 一、什么是动态规划 从本质上来说,动态规划就是递推,我们先来看一个有关地推的例子。 例题1、 斐波那契数列 输入\(n\), 求斐波那契数列的第n项 我们在上小学的时候就知道,斐波那契数列的递推式是 \[ f(n) = f(n-1) + f(n-2), f(1) = f(2) = 1 \] 要计算第n项,需要先知道第n-1项和n-2项。要知道第n-1项就要知道n-2和n-3项……直到遇到边界条件f(1)和f(2)。那么反过来说,知道了第1项和第2项,就能知道第3项,第4项及以后。 为什么我要从两种角度说明呢,因为这两种角度正是设计和编写动态规划算法的两种思路和实现方式 第一种角度是从后往前推,用递归实现 123int f(int x) { return x == 1 || x == 2 ? 1 : f(x-1) + f(x-2);} 上面的代码有一个问题:当n教大的时候,运行时间会非常长。因为其中存在重复计算的问题。比如计算...
在win10环境下配置Hexo博客
首先贴上几个链接 官方文档:https://hexo.io/zh-cn/docs/ 推荐的视频: https://www.bilibili.com/video/av44544186 https://www.bilibili.com/video/av24897960 接下来我们开始安装 安装 Node.js Hexo博客是基于node.js 框架的,所以首先要安装nodejs。下面给出链接 https://nodejs.org/en/ 1563369322945 可以用下面的命令查看是否安装成功 1node -v 安装 git https://git-scm.com/downloads 传送门如上 安装一直点下一步就可以了, 安装hexo 创建一个放博客的文件夹 启动管理员权限的cmd,输入下面指令安装hexo 1npm install -g hexo-cli 在blog所在的文件夹里输入 1hexo init 然后一个 Hello World的博客就初始化完成了 使用博客 下面的命令很常用 12345hexo clean #清除缓存 ...
cuda-programming
CUDA Programming https://github.com/ForceInjection/AI-fundermentals Getting Started 开发环境与工具链:CUDA GPU、驱动、CUDA Toolkit、C 编译器等。 在windows下需要安装 nvidiasmi, nvcc, visual stuido 2022, 检测: 12nvidia-sminvcc --version 然后新建一个CUDA template项目,运行一下,可以跑通就可以 Introduction to CUDA C 第一个 CUDA 程序、kernel 调用、传参、查询设备、使用 device properties。 不能用 format 因为 cuda 对 std的支持不好 1234567891011121314151617181920212223242526272829303132333435363738394041#include <cstdio>#include <cuda_runtime.h>#include <source_lo...
邮件服务器
邮件服务器 添加邮件用户 1sudo adduser alice 修改 1sudo vim /etc/postfix/virtual_sender_maps 添加 12# 允许 alice 用户发送的地址列表alice@fyind.de alice 更新 Postfix 的数据库文件(关键步骤! 每次修改完 virtual_sender_maps 都必须运行此命令。 重启 Postfix 以加载新的授权规则 12sudo postmap /etc/postfix/virtual_sender_mapssudo systemctl restart postfix
虚拟机
虚拟机 Emulation 指令集模拟是在一个平台上模拟另一个(或同一)CPU 的指令与执行语义。常见场景包括:跨架构仿真(比如在 x86 上跑 ARM 二进制)、系统模拟(Bochs)、动态二进制分析 Interpretation 解释执行(Interpretation):逐条取出目标指令,解析并执行对应的宿主(host)操作。 simple interpreter 是一种执行程序的方法,它不直接在硬件上运行目标二进制,而是 逐条读取(decode)、理解(dispatch)、执行(interpret)指令的语义。Decode-and-Dispatch 模式 核心机制:有一个大循环(interpreter loop),每次循环: 取指 (fetch):从“程序计数器(PC)”指向的内存里读一条指令。 解码 (decode):解析这条指令是什么类型(加法?加载?跳转?)。 分发 (dispatch):根据指令类型,跳转到对应的解释函数/分支逻辑。 执行 (execute):修改解释器内部维护的状态(寄存器、内存、标志位等)。 更新 PC:让 PC 指向下一条指令,然后继续循环...
机器学习实战
输入数据集合 导入CSV 1234567import pandas as pddf = pd.read_csv( "book_sales.csv", index_col='Date', parse_dates=['Date'],) 返回一个 Dataframe 类型 index_col 把 Date 这一列设置为 DataFrame 的索引(行标签) parse_dates 把 Date 这一列解析为 日期类型(datetime),而不是普通字符串。 period 1tunnel = tunnel.to_period() 默认 Pandas 使用 DatetimeIndex(时间戳,表示一个具体时刻)。 .to_period() 转换为 PeriodIndex(时间段,表示一个统计周期,比如“2020-01”表示整个 1 月)。 在一些时间序列分析场景下,PeriodIndex 更直观和方便,比如按月份、季度分析数据。 DataFrame 信息查看 df.index index的那一列 去除一列...
Rowhammer攻击
Rowhammer 攻击 Rowhammer 攻击是一种硬件漏洞,允许攻击者通过反复激活(即“锤击”)一个或多个相邻内存行来在无关的物理内存行中翻转比特 原理 Rowhammer 漏洞的核心是 DRAM 干扰错误 (DRAM disturbance errors)。当攻击者反复高速访问 (或“锤击”) 内存中的一个或多个行时,其相邻的内存行可能会因为电磁干扰等物理效应而发生 比特翻转 (bit flips) 攻击过程 (传统): ◦ 锤击 (Hammering):攻击者重复访问(读或写)内存中的特定“攻击者行 (aggressor rows)”。 ◦ 比特翻转 (Bit Flips):由于DRAM单元之间的物理距离和电荷泄漏等问题,被锤击行的相邻“受害者行 (victim rows)”中的比特可能会从 0 翻转到 1,或从 1 翻转到 0。 ◦ 目标数据:攻击者通常会设法让受害者行包含有价值的数据,例如 页表项 (Page Table Entries, PTEs)。通过翻转 PTE 中的比特,攻击者可以修改内存映射,从而获得对整个物理内存的读写权限,实现权限升级 攻击演变与挑战:...
C++高性能编程
目录 一、开发环境配置 CMake与编译环境 C++23新特性 二、内存管理与优化 内存管理基础 内存中的对象 内存所有权 自定义内存管理 三、模板元编程 模板元编程基础 Type Traits类型萃取 编译期编程 异构容器与变参模板 四、并发与并行编程 并发编程基础 线程与同步 无锁编程 性能优化指南 五、实践练习 并行编程练习 一、开发环境配置 CMake g++14 支持C++23需要g++14版本,可以安装 1sudo apt install gcc-14 g++-14 Cmake 新建 CMakeLists.txt 里面写 12345678cmake_minimum_required(VERSION 3.28)set(CMAKE_CXX_COMPILER g++-14)set(CMAKE_CXX_STANDARD 23)project(exampleproject LANGUAGES CXX)add_executable(exampleproject main.cpp) 构建 优点: - 明确指定源代码和构建目录 - 避免在源代码目录中生成构建文...