理论计算机学
Formale Sprachen
语言问题(Wortproblem):给定一个字符串,这个字符串是由某个语法生成的吗?也就是它是否符合某个语法规则。
识别器(Recognizer): 一个能解决对应语法的语言问题的抽象
基本概念
定义2.1
一个字母表(Alphabet) \(\Sigma\) 是一个有限集合。比如 ASCII, Unicode
一个语句(Wort/String) 是从字母表中组合出的有限字母序列,比如 010
\(|w|\) 指代语句的长度
空字符串是 $$
若 \(u,v\) 是语句,那么 \(uv\) 是它们的组合(Konkatenation)
若 \(w\) 是一个语句,那么 \(w^{n}\) 是如下定义的: \[ w^{0}=\epsilon \text { , } w^{n+1}=w w^{n} . \text { Bsp: }(a b)^{3}=a b a b a b \]
\(\Sigma ^{*}\) 是字符集 \(\Sigma\) 的所有语句
子集 \(L \subseteq \Sigma^{*}\) 是一个语言(formale Sprache)
定义2.3 语言的操作
- 连接: \(AB = \{uv | u \in A \land v \in B\}\)
\[ \begin{array}{l} \text { Bsp: }\{a b, b\}\{a, b b\}=\{a b a, a b b b, b a, b b b\} \\ \text { NB: }\{a b, b\} \times\{a, b b\}=\{(a b, a),(a b, b b),(b, a),(b, b b)\} \end{array} \]
- \(A^{n}=\left\{w_{1} \cdots w_{n} | w_{1}, \ldots, w_{n} \in A\right\}=\underbrace{A \cdots A}_{n}\)
- \(A^{*}=\left\{w_{1} \cdots w_{n} | n \geq 0 \wedge w_{1}, \ldots, w_{n} \in A\right\}=\bigcup_{n \in N } A^{n}\)
- \(A^{+}=A A^{*}=\bigcup_{n \ge 1} A^{n}\)
计算规则
- \(\emptyset A=\emptyset\)
- \(\{\epsilon\} A=A\)
- \(A(B \cup C)=A B \cup A C\)
- \((A \cup B) C=A C \cup B C\)
- \(A^{*} A^{*}=A^{*}\)
定义 2.7 语法
一个语法(Grammatik)是4元组 \(G = (V, \Sigma, P, S)\)
\(V\) 是变量符号集合(Menge von Nichtterminalzeichen), 它是组织语言的字符。
\(\Sigma\) 是字符集(Menge von Terminalzeichen)
\(P \subseteq(V \cup \Sigma)^{*} \times(V \cup \Sigma)^{*}\) 是Produktionen的有限集合
\(S \in V\) 是其实字符
一些约定
\(A, B, C, \ldots\) 和 \(\langle\text { Term }\rangle,\langle\text { Faktor }\rangle\)是 Nichtterminale,
\(a, b, c, \ldots\) 是Terminale
\(\alpha, \beta, \gamma, \ldots \in(V \cup \Sigma)^{*}\)
Produktion 写成 \(\alpha \rightarrow \beta\) ,代替 \((\alpha, \beta) \in P\)
多个Produktion:\(\alpha \rightarrow \beta_{1}|\cdots| \beta_{n}\)
比如算数表达式
\(V=\{\langle E x p r\rangle,\langle\text { Term }\rangle,\langle F a k t o r\rangle\}\)
\(\Sigma=\{a, b, c,+, *,(,)\}\)
\(S=\langle E x p r\rangle\)
\(P\) 如下: \[ \begin{aligned} \langle Expr \rangle & \rightarrow\langle\text { Term }\rangle \\ \langle Expr \rangle & \rightarrow\langle Expr \rangle+\langle\text { Term }\rangle \\ \langle Term \rangle & \rightarrow\langle Factor \rangle \\ \langle Term \rangle & \rightarrow\langle\text { Term }\rangle *\langle Factor \rangle \\ \langle Factor \rangle & \rightarrow a|b| c \\ \langle Factor \rangle & \rightarrow(\langle Expr \rangle) \end{aligned} \]
定义2.9
一个语法 \(G=(V, \Sigma, P, S)\) 有一个推导关系 (Ableitungsrelation) \(\rightarrow _{G}\) 在\(V \cup \Sigma\) 上: \[ \alpha \rightarrow_{G} \alpha^{\prime} \] 当且仅当: \(P\) 里有一个规则 \(\beta \rightarrow \beta^{\prime}\) 和语句 \(\alpha_{1}, \alpha_{2}\),使得 \[ \alpha=\alpha_{1} \beta \alpha_{2} \quad \text { und } \quad \alpha^{\prime}=\alpha_{1} \beta^{\prime} \alpha_{2} \] 比如,下面的两个表达式可以互相转换(Term可以拆开来看,也可以组合起来看): \[ a+\langle\text { Term }\rangle+b \quad \rightarrow_{G} \quad a+\langle\text { Term }\rangle *\langle\text { Factor }\rangle+b \] 一个序列 \(\alpha_{1} \rightarrow_{G} \cdots \rightarrow_{G} \alpha_{n}\) 是从 \(\alpha _{1}\) 到 \(\alpha _{n}\) 的推导(Ableitung)
若 \(\alpha_{1}=S\) 且 \(\alpha_{n} \in \Sigma^{*}\) 那么 \(G\) 生成了(erzeugt) \(\alpha_{n}\)
\(G\) 的语言是所有 \(G\) 能生成的语句的集合, 记为 \(L(G)\)
定义2.12 推导的迭代
也就是推导多次的关系: \[ \begin{array}{c} \alpha \rightarrow_{G}^{0} \alpha \\ \alpha \rightarrow_{G}^{n+1} \gamma \quad: \Leftrightarrow \quad \exists \beta . \alpha \rightarrow_{G}^{n} \beta \rightarrow_{G} \gamma \end{array} \] 写成闭包: \[ \alpha \rightarrow_{G}^{*} \beta \quad: \Leftrightarrow \quad \exists n . \alpha \rightarrow_{G}^{n} \beta \\ \alpha \rightarrow_{G}^{+} \beta \quad: \Leftrightarrow \quad \exists n>0 . \alpha \rightarrow_{G}^{n} \beta \] 于是语言的定义还可以这样: \(L(G)=\left\{w \in \Sigma^{*} | S \rightarrow_{G}^{*} w\right\}\)
乔姆斯基谱系(Chomsky-Hierarchie)
一个语法 \(G\) 是:
- Typ 0 (Phrasenstrukturgrammatik )全部都是
- Typ 1 (Kontextsensitive Grammatik)若对于每个Produktion \(\alpha \rightarrow \beta\) 除了\(S \rightarrow \epsilon\) 满足 \(|\alpha| \leq|\beta|\)。也就是每次不会减少长度
- Typ 2 (Kontextfreie Grammatik)若它是Typ 1 且对于每个 Produktion \(\alpha \rightarrow \beta\),满足\(\alpha \in V\)
- Typ 3 ( Rechtslineare Grammatik)若是 Typ 2, 若对于每个Produktion \(\alpha \rightarrow \beta\) 除了\(S \rightarrow \epsilon\) 满足 \(\beta \in \Sigma \cup \Sigma V\)
正则表达式
定义3.1 确定有限自动机Deterministische endliche Automaten(DFA)
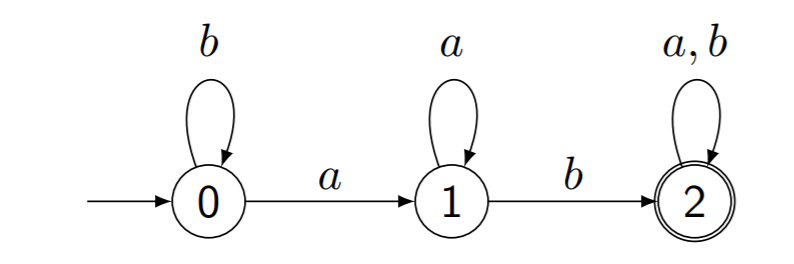
\(M=\left(Q, \Sigma, \delta, q_{0}, F\right)\) 是一个确定有限状态自动机
有限的状态集合 \(Q\)
有限的输入字符集Eingabealphabet \(\Sigma\)
一个完全(total)的传递函数 \(\delta: Q \times \Sigma \rightarrow Q\)
一个开始状态 \(q_0\)
终止状态的集合 \(F \subseteq Q\)
定义3.2 语言
被 \(M\) 接受的语言是 \[ L(M):=\left\{w \in \Sigma^{*} \mid \hat{\delta}\left(q_{0}, w\right) \in F\right\} \] 其中 \(\hat{\delta}: Q \times \Sigma^{*} \rightarrow Q\) 是递归定义的: \[ \begin{aligned} \hat{\delta}(q, \epsilon) &=q \\ \hat{\delta}(q, a w) &=\hat{\delta}(\delta(q, a), w) \text { für } a \in \Sigma, w \in \Sigma^{*} \end{aligned} \] 一个语言是正则的(regulär),当且仅当它被一个 \(DFA\) 所接受
\(\hat{\delta}\) 的性质
- \(\hat{\delta}(q, a)=\delta(q, a)\)
- \(\hat{\delta}(q, w a)=\delta(\hat{\delta}(q, w), a)\)
定义3.8 非确定有限自动机(NFA)
\(N=\left(Q, \Sigma, \delta, q_{0}, F\right)\) 是一个非确定有限自动机
- \(Q,\Sigma,q_0,F\) 和DFA一样
- \(\delta: Q \times \Sigma \rightarrow \mathcal{P}(Q)\)
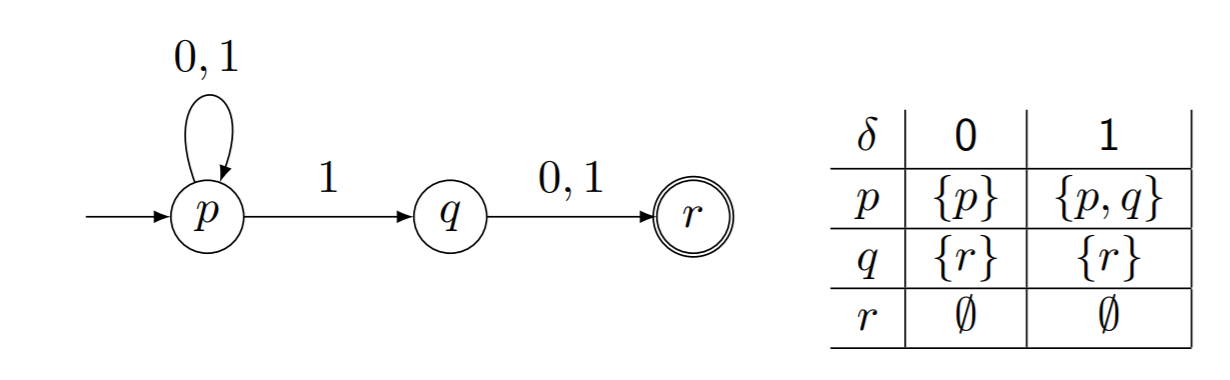
定理 3.9 rechtslineare Grammatik和NFA
对于每个rechtslineare Grammatik \(G\) 存在一个 NFA \(M\) 使得 \[ L(G)=L(M) \]
定理 3.10 DFA和NFA
对于每个NFA \(N\) 存在一个 DFA \(M\) 使得 \[ L(N) = L(M) \]
定理 3.12 DFA 的状态
\[ L_{k}:=\left\{w \in\{0,1\}^{*} \mid \text { das } k \text {-letzte Bit von } w \text { ist } 1\right\} \]
每个 DFA \(M\),且 \(L(M)=L_k\) 有至少 \(2^{k}\) 个状态
定理 3.13 DFA和 G
对于每个 DFA \(M\) , 存在一个 rechtslineare Grammatik \(G\) 使得 \[ L(M) = L (G) \]
定义 3.15 (\(\epsilon\)-NFA)
一个 NFA 带有 \(\epsilon\)-传递 (\(\epsilon\)-NFA) 是一个 NFA, 它带有一个特殊字符 \(\epsilon \notin \Sigma\) \[ \delta: Q \times(\Sigma \cup\{\epsilon\}) \rightarrow \mathcal{P}(Q) \]
定理3.16 (\(\epsilon\)-NFA)和 NFA
对于每个 \(\epsilon\)-NFA \(N\) 存在一个 NFA \(N'\) 使得 \(L(N)=L(N')\)
定义 3.19 正则表达式
正则表达式是归纳定义的:
\(\empty\) 是一个正则表达式
\(\epsilon\) 是一个正则表达式
对于每个 \(a \in \Sigma\) 是一个正则表达式
当 \(\alpha,\beta\) 是正则表达式时
- \(\alpha \beta\)
- \(\alpha | \beta\)
- \[\alpha ^{*}\]
是正则表达式
其他都不是正则表达式
定义 3.20 正则表达式的语言
对于一个正则表达式 \(\gamma\) ,\(L(\gamma)\) 如下定义 \[ \begin{array}{l} L(\emptyset)=\emptyset \\ L(\boldsymbol{\epsilon})=\{\epsilon\} \\ L(a)=\{a\} \\ L(\alpha \beta)=L(\alpha) L(\beta) \\ L(\alpha \mid \beta)=L(\alpha) \cup L(\beta) \\ L\left(\alpha^{*}\right)=L(\alpha)^{*} \end{array} \]
定理 3.23 Kleene
一个语言\(L \subseteq \Sigma^{*}\)可以通过正则表达式表达,当且仅当它是正则的
定理 3.34 运算
若 \(R, R_{1}, R_{2} \subseteq \Sigma^{*}\) 是正则语言,那么 \[ R_{1} R_{2}, R_{1} \cup R_{2}, R^{*}, \bar{R}\left(:=\Sigma^{*} \backslash R\right), R_{1} \cap R_{2}, R_{1} \backslash R_{2} \] 也是正则语言
定理 3.25
若 \(M_{1}=\left(Q_{1}, \Sigma, \delta_{1}, s_{1}, F_{i}\right)\) 和 \(M_{2}=\left(Q_{2}, \Sigma, \delta_{2}, s_{2}, F_{2}\right)\) 都是DFA 那么他们的乘法自动机Produkt-Automat是 \[ \begin{array}{c} M:=\left(Q_{1} \times Q_{2}, \Sigma, \delta,\left(s_{1}, s_{2}\right), F_{1} \times F_{2}\right) \\ \delta\left(\left(q_{1}, q_{2}\right), a\right):=\left(\delta_{1}\left(q_{1}, a\right), \delta_{2}\left(q_{2}, a\right)\right) \end{array} \] 是 DFA, 它接受 \(L\left(M_{1}\right) \cap L\left(M_{2}\right)\)
定义 3.26 等价
两个正则表达式是等价的,当且仅当他们有相同的语言 \[ \alpha \equiv \beta: \Leftrightarrow L(\alpha)=L(\beta) \]
定理 3.27 0和1
\[ \begin{array}{l} \emptyset|\alpha \equiv \alpha| \emptyset \equiv \alpha \\ \emptyset \alpha \equiv \alpha \emptyset \equiv \emptyset \\ \epsilon \alpha \equiv \alpha \epsilon \equiv \alpha \\ \emptyset^{*} \equiv \epsilon \\ \epsilon^{*} \equiv \epsilon \end{array} \]
定理3.28 运算法则
- 结合律
\[ \begin{array}{l} (\alpha \mid \beta)|\gamma \equiv \alpha|(\beta \mid \gamma) \\ (\alpha \beta) \gamma \equiv \alpha(\beta \gamma) \end{array} \]
- 交换律
\[ \alpha|\beta \equiv \beta| \alpha \]
- 分配率
\[ \begin{array}{l} \alpha(\beta \mid \gamma) \equiv \alpha \beta \mid \alpha \gamma \\ (\alpha \mid \beta) \gamma \equiv \alpha \gamma \mid \beta \gamma \end{array} \]
- 幂等元
\[ \alpha \mid \alpha \equiv \alpha \]
定理 3.29 运算法则2
\[ \begin{array}{c} \boldsymbol{\epsilon} \mid \alpha \alpha^{*} \equiv \alpha^{*} \\ \alpha^{*} \alpha \equiv \alpha \alpha^{*} \\ \left(\alpha^{*}\right)^{*} \equiv \alpha^{*} \end{array} \]
定理 3.31 Redko
不存在有限的等价关系集合,从中可以推出其他所有的等价关系
定理 3.32 Pumping Lemma fur reguläre Sprachen
若 \(R \subseteq \Sigma^{*}\) 是正则的,那么存在一个 \(n>0\) ,使得每个 \(z \in R\) 且 \(|z| \ge n\) 可以分解为 \(z=uvw\), 其中
- \(v \ne \epsilon\)
- \(|u v| \leq n\)
- \(\forall i \geq 0 . u v^{i} w \in R\)
定理 3.33 非正则1
语言\(\left\{a^{i} b^{i} \mid i \in \mathbb{N}\right\}\) 不是正则的
定理 3.34 非正则2
语言\(L=\left\{0^{m^{2}} \mid m \geq 0\right\}\) 不是正则的
定理 3.35 括号式子
通过括号 \(\{(,)\}\) 括起来的式子不是正则的
定理3.36 数学公式
数学公式 arithmetischen Ausdrücken 不是正则的
定义 3.37 问题分类
设 \(D\) 是一个 DFA, NFA, RE, rechtslineare Grammatik ...
- Wortproblem: 给定 \(w\) 和 \(D\) ,是否 \(w \in L(D)\)
- Leerheitsproblem : 给定 \(D\) , 是否 \(L(D) = \empty\)
- Endlichkeitsproblem: 给定 \(D\) , \(L(D)\) 是否有限
- Äquivalenzproblem:给定 \(D_1, D_2\) 是否满足 \(L(D_1) \equiv L(D_2)\)
定理 3.38 Wortproblem
给定 \(w\) 和 DFA \(M\), Wortproblem是可以在 \(O(|w|+|M|)\) 确定的
定理 3.39 Wortproblem
给定 \(w\) 和 NFA \(N\), Wortproblem是可以在 \(O(|Q|^2|w|+|N|)\) 确定的
定理 3.40 Leerheitsproblem
对于 NFA和DFA, Leerheitsproblem可以分别在时间\(O\left(|Q|^{2}|\Sigma|\right)\) 和 \(O\left(|Q||\Sigma|\right)\) 中确定
定理 3.41 Endlichkeitsproblem
对于 DFA和NFA,Endlichkeitsproblem是可以确定的
定理3.42 Aquivalenzproblem
对于DFA, Aquivalenzproblem 是可以确定的
定理 3.43 Aquivalenzproblem 时间
对于 DFA, Aquivalenzproblem 可以在\(O\left(\left|Q_{1}\right|\left|Q_{2}\right||\Sigma|\right)\) 中确定
定理 3.44
对于NFA, Aquivalenzproblem 可以在 \(O\left(2^{\left|Q_{1}\right|+\left|Q_{2}\right|}\right)\) 中确定
定理 3.45
对于正则表达式,Aquivalenzproblem 是可以确定的
定理3.47 Ardens Lemma
\[ X \equiv \alpha X \mid \beta \quad \Longrightarrow \quad X \equiv \alpha^{*} \beta \]
用于解方程,解出正则表达式
Minimierung endlicher Automaten

首先×掉所有终止状态和非终止状态的对,然后考虑每个对,看它下一个位置是不是一样的。如果有不一样的就x掉.
Definition 3.52 (Äquivalenz von Zuständen)
\[ p \equiv{ }_{M} q \quad \Leftrightarrow \quad\left(\forall w \in \Sigma^{*} . \hat{\delta}(p, w) \in F \Leftrightarrow \hat{\delta}(q, w) \in F\right) \]
定理 3.56
若 \(M\) 是 DFA且没有无法到达的状态,那么 \(M / \equiv\) 是最小的DFA
Satz 3.60 (Myhill-Nerode)
一个语言是正则的,当且仅当它有有限个等价类
Kontextfreie Sprache
定义 4.18
一个 CFG \(G\) 是mehrdeutig 的,若有一个 \(w\) ,它的Syntaxbaum有多个
定理 4.20
\[ \left\{a^{i} b^{j} c^{k} \mid i=j \vee j=k\right\} \]
是mehrdeutig 的
Chomsky-Normalform
只有 \[ A \rightarrow a \quad \text { oder } \quad A \rightarrow B C \]
\(\epsilon\)-Produktion
\[ A \rightarrow \epsilon \]
Kettenproduktion
\[ A \rightarrow B \]
构造Chomsky-Normalform
- 对于每个 \(a\) 构造 \(A \rightarrow a\)
- \(A\rightarrow BCD\) 换成 \(A \rightarrow KD ,K \rightarrow BC\)
- 消除所有 \(\epsilon\)-Produktion
- 消除所有 Kettenproduktion
Satz 4.29 (Pumping-Lemma)
对于 kontextfreie Sprache \(L\) 存在一个 \(n \ge 1\) 使得 \(z \in L\) 且 \(|z|\ge n\) 分解成 \[ z=u v w x y \] 使得 \[ \begin{aligned} &v x \neq \epsilon \\ &|v w x| \leq n, \text { und } \\ &\forall i \in \mathbb{N} . u v^{i} w x^{i} y \in L \end{aligned} \]
Abschlusseigenschaften
CFG 是对于 \[ \begin{aligned} &L\left(G_{1}\right) \cup L\left(G_{2}\right) \\ &L\left(G_{1}\right) L\left(G_{2}\right) \\ &\left(L\left(G_{1}\right)\right)^{*} \\ &\left(L\left(G_{1}\right)\right)^{R} \end{aligned} \] 闭合
但是对于交集和补集不是
\(L_{1}:=\left\{a^{i} b^{i} c^{j} \mid i, j \in \mathbb{N}\right\}\) ist kontextfrei
\(L_{2}:=\left\{a^{i} b^{j} c^{j} \mid i, j \in \mathbb{N}\right\}\) ist kontextfrei
\(L_{1} \cap L_{2}=\left\{a^{i} b^{i} c^{i} \mid i \in \mathbb{N}\right\}\) ist nicht kontextfrei
4.6 Algorithmen fur kontextfreie Grammatiken
- nützlich 存在从 \(S\) 推导出字符,其中 \(X\) 出现
- erzeugend 从 \(X\) 可以推导出 \(w\)
- erreichbar 从\(S\) 可以到大 \(X\)
nützlich 符号是erzeugend 和erreichbar
Satz 4.36 减少 CFG
- 消除 nicht erzeugend 符号
- 消除 nicht erreichbar 符号
定理 4.37
erzeugend 符号的集合, erreichbaren 符号的集合是可计算的
定理 4.39
CFG \(G\) 是否是 \(\emptyset\) 是可以决定的
CYK

栈自动机PDA
可以操控一个栈并且push和pop的自动机
DPDA
\[ |\delta(q, a, Z)|+|\delta(q, \epsilon, Z)| \leq 1 \]
要么每个字符只有一个,要么只有一个\(\epsilon\)
DCGF
被 DPDA接受的CFG
每个正则语言都是 DCFG
Satz 4.66
DCFG 对于补集操作闭合
DCFL不是多意性的
Satz 4.70
Das Wortproblem fur DCFLs ist in linearer Zeit 可解决

可决定性可计算性
对于一个函数 \(f:A\rightarrow B\)
- total 对于所有 \(a\in A\), \(f(a)\) 有定义
- partiell \(f(a)\) 可以没有定义
- echt partiell 不是total的
图灵机TM
有状态,可以操控指针左移右移
如果没有状态了就停止
Satz 5.22 (WHILE → TM)
Jede WHILE-berechenbare Funktion ist auch Turing-berechenbar.
Fakt 5.23 (WHILE → GOTO)
Satz 5.24 (GOTO → WHILE)
Satz 5.27 (TM → GOTO)
5.2 Unentscheidbarkeit des Halteproblems
可决定性
若 \[ \chi_{A}(x):= \begin{cases}1 & \text { falls } x \in A \\ 0 & \text { falls } x \notin A\end{cases} \] 可计算
定义 5.31
\(M[w]\) 是 \(M\) 输入 \(w\)
\(M[w] \downarrow\) 是 \(M\) 输入 \(w\) 并且停止了
Definition 5.32 (Spezielles Halteproblem)
给定 \[w \in \{0,1\}^{*}\], \(M_{w}[w]\)是否能停止
Satz 5.33
Das spezielle Halteproblem ist nicht entscheidbar.
Definition 5.34 ((Allgemeines) Halteproblem)
给定 \[w,x \in \{0,1\}^{*}\], \(M_w[x]\) 是否能停止
Das Halteproblem H ist nicht entscheidbar.
Definition 5.36 (Reduktion)
Eine Menge\(A \subseteq \Sigma^{*}\) ist reduzierbar auf eine Menge\(B \subseteq \Gamma^{*}\) gdw es eine totale und berechenbare Funktion\(f: \Sigma^{*} \rightarrow \Gamma^{*}\) gibt mit \[ \forall w \in \Sigma^{*} . w \in A \Leftrightarrow f(w) \in B \] 写作 \[ A\le B \] Falls \(A \leq B\) und \(B\) ist entscheidbar, so ist auch \(A\) entscheidbar.
Satz 5.40
Das Halteproblem auf leerem Band, \(H_0\), ist unentscheidbar \[ H_{0}:=\left\{w \in\{0,1\}^{*} \mid M_{w}[\epsilon] \downarrow\right\} \]
Satz 5.48 (Rice)
\(F\) 是可计算函数的集合
trivial: \(F=\emptyset, F= alle\)
Alle nicht-triviale semantische Eigenschaften von Programmen sind unentscheidbar.
Satz 5.50 (Rice-Shapiro)
Die Menge der terminierenden Programme ist nicht semi-entscheidbar.
Die Menge der nicht-terminierenden Programme ist nicht semi-entscheidbar.
可以一个一个尝试
Definition 5.52 (Postsche Korrespondenzproblem, Post’s Correspondence Problem, PCP)
Das PCP ist semi-entscheidbar.
Satz 5.61
对于 CFG 下面的问题是不可决定的
- G 多意性
- L(G) 正则
- DCFL
复杂度理论
P问题
存在DTM在多项式时间内解决
NP问题
存在NTM在多项式时间内解决
Satz 6.10
A ∈ NP gdw es gibt polynomiell beschränkten VerifikaSatz 6.10tor für A.
NP完全
polynomiell reduzierbar
\[ A \leq_{p} B \]
NP-hart
\(L\) 是NP-hart,当且仅当对于所有 \(A\in NP\), \(A \leq_{p} L\)
NP 完全
\(L \in NP\) 是 NP-hart
SAT
一个逻辑式子是否可以被满足
3KNF-SAT
\[ K_{1} \wedge \cdots \wedge K_{n} \]
每个里面只有3个变量


